
The "usual" 120 Polyhedron, or, the one we have labeled as "the" 120 Polyhedron, is essentially the rhombic Triacontahedron with its face centers pushed out.

|

|
| The 120 Polyhedron and the rhombic triacontahedron | |
This was done to accommodate 5 Octahedra. (An Octahedron has 6 vertices. So, 5 Octahedra will have 6x5=30 vertices, one for each of the 30 faces of the rhombic Triacontahedron.)
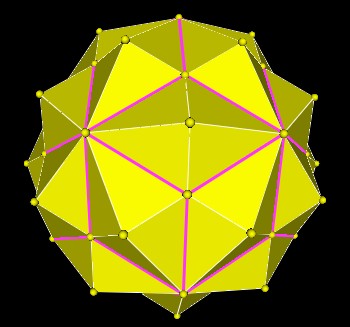
However, the complex of 5 intersecting Octahedra by itself has 120 trianglular faces. Therefore, it is another candidate for Lynnclaire Dennis' "120 Polyhedron".
Here is the build-up of the 5 Octahedra.
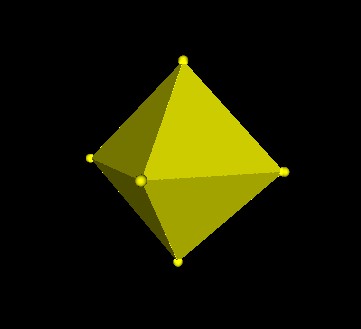

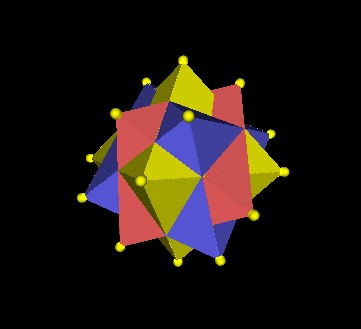
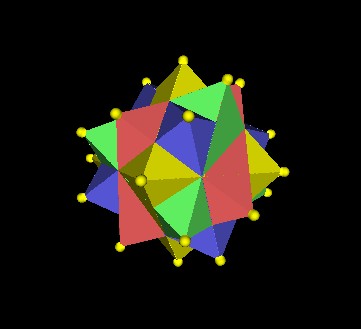

As you can see, there are 4 triangular faces around each vertex. So there are 4x30=120 triangular faces.
Each of the 5 Octahedra can be considered to be a Jitterbug.
Here are some pictures of the paths that the vertices of a single Jitterbug trace out.
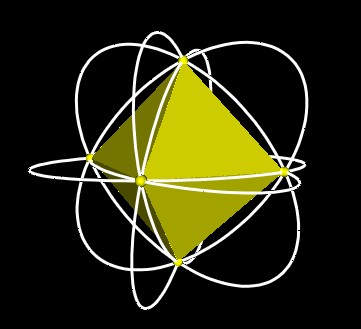
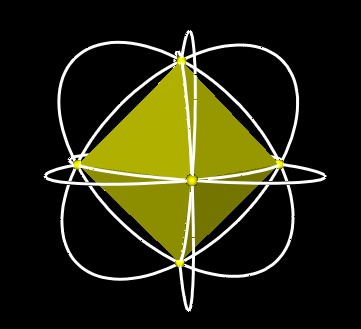
All the paths from all 5 Jitterbugs is shown in the next figures.
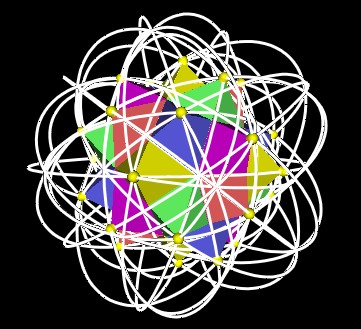

And here is an animation which will show all the vertices of the 5 Jitterbugs following long these paths.
Lynnclaire has said that suring the dynamic motion of the 120 Polyhedron, there is energy expelled through opennings that form in the polyhedron. The energy is emitted through one type of vertex and is taken back in through another type of vertex. This is exactly the kind of phenomena we see here. As the triangles of the Jitterbug rotate and move radially, their vertices seem to emerge through the Icosahedron-type vertices, follow a curved path, and sbumerge into Dodecahedron-type vertices.
Of course, by reversing the animations you will see the yellow spheres of the Jitterbug vertices emerge from the Dodecahedron-type vertices and return into the Icosahedron-type vertices.
Here is an animation showing both the Icosahedron and the Dodecahedron.
And here is an animation showing just the Jitterbug vertex spheres.
The motion that Lynnclaire is attempting to describe is more complex than shown here. In addition, there is a rotational motion which appears to distort the spherical symmetry of the system she is describing. This has not been included here.
Here is the "usual" 120 Polyhedron and the Jitterbug ellipses.


Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.