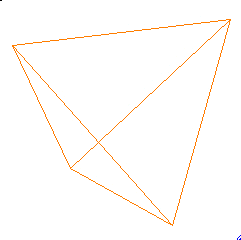
Lynnclaire once pointed out to me that if you build the pattern out of wire you can push on this wire model in such a way that it will open up and reveal 4 open areas. It was suggested that this fully expanded form might be analogous to a tetrahedron.
I have discovered that it fits exactly a tetrahedron. I show here how to map the pattern onto a tetrahedron.
First, of course, start with a tetrahedron. (The orientation of the following image is so that all facets of the tetrahedron can be seen.)

Next, join all the mid-edges together. This defines an octahedron inside the tetrahedron. Dividing the edges of the tetrahedron into 2 halfs results in what is called a 2-frequency tetrahedron.
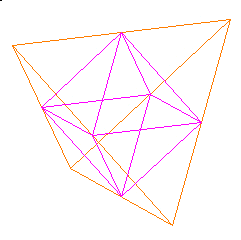
Now draw a circle on each of the tetrahedron's 4 faces.

Now we need to trim each of the 4 circles as shown in the following illustration. (Note that we are removing 120 degrees from each of the 4 circles.)
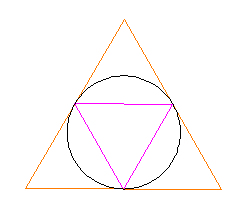
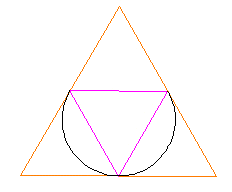
We do this now for each of the 4 circles. It is important to trim just the right part of each of the circles so that the pattern will emerge.

The result is the pattern in its open position. Note that the 2 "cross over/under" points are at the top and bottom of this illustration and are located at the mid-edge points of 2 of the tetrahedron's edges.

Here is a movie which might help you get a better feel for it.

And here are 2 familar perspectives...

I hope this helps to clarify Lynnclaire's knot pattern in its open position.
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.