Rotation of Dodecahedron's Edges

While exploring Marvin Solit's 6 Pentagon Tensegrity Sphere (6-PTS), I found that the rotation of the regular Dodecahedron's 30 edges will pass through phases which define the (6-PTS) and on to the definition of 5 intersecting Teterahedra. I had previously explored the 5 Tetrahedra with a regular Dodecahedron, as described in the "What's in this polyhedron?" article.

Here is a (low quality) gif animation of the edges of the regular dodecahedron rotating, and moving radially inward, to come come to the definition of 5 Tetrahedra.

Click here for a better quality animation (which also lets you step through the animation frame by frame) but which takes a long time to download.

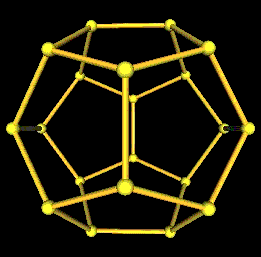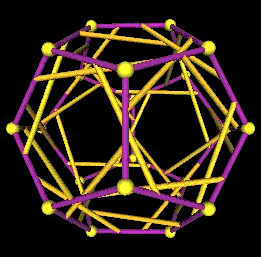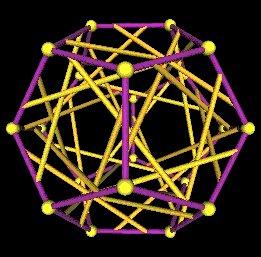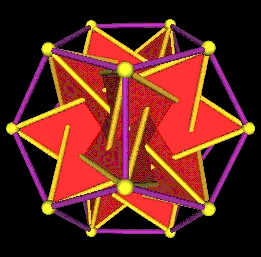
Here are some images of the 5 Tetrahedra in the regular Dodecahedron from different points of view.

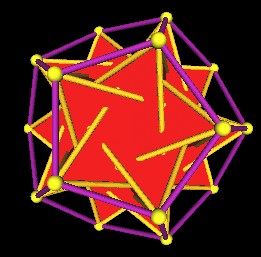
One set of 5 Tetrahedra in the regular Dodecahedron.

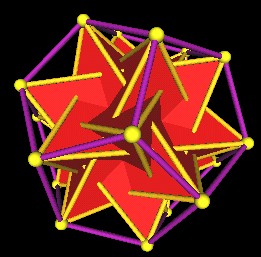
One set of 5 Tetrahedra in the regular Dodecahedron.

A little more detail....

The regular Dodecahedron has 30 edges.

We can pass a rotation axes through each of the 30 edges at their mid edge points.

As the edges rotate, in the animations I have done here, I have adjusted the edge lengths as well as moved them radially inward so that the 2 ends of any of the rotating edges move along the line (edges) of the regular Dodecahedron.

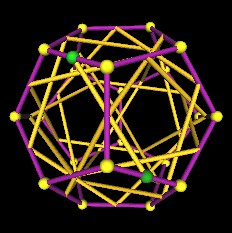
Now, at the half-way point, when the ends of the rotating edges areat the mid-edge points of the Dodecahedron's edges, 6 pentagons are defined.

Marking 2 mid-edge points.

Here are some images with the rotating edges in this 6 pentagon position.

6 Pentagons.

6 Pentagons.

This is the same configuration as the 6 pentagon tensegrity spheres, although in the tensegrity model, the ends of the struts do not touch.

6 Pentagonal Tensegrity Sphere.

Here is an attempt to make at least one of the pentagons more clearly visible.

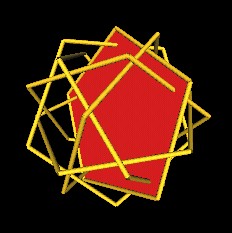
6 Pentagons, 1 filled in.

The angle of rotation to position the 30 edges of the regular Dodecahedron into this 6 Pentagon Tensegrity Sphere configuration is approximately 31.7 degrees.

To position the 30 edges into the 5 Tetrahedron configuration requires a rotation of 45.0 degrees.

If we continue to rotate the edges through 90 degrees, the Icosahedron is defined.

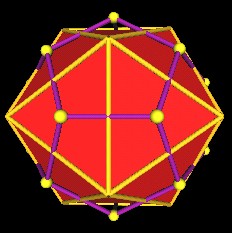
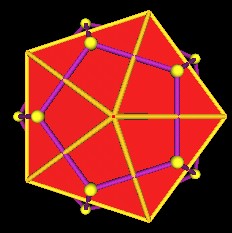
Icosahedron has 30 edges rotated 90 degrees to the Dodecahedron.

Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.