Why I Don't Believe Searl's Law Of Squares
I will explain here why I don't believe that
Searl's use of Magic Squares and his Law of Squares has anything to do with the
physics involved in his devices.
In short, I don't think the use of Magic
Squares has any significance to the construction of his devices because:
1. He doesn't specify what units the materials are to be
measured in. He says at one point that the numbers in the Square used is the
mass of the material and at another point he say it’s the volume of the
material. Very different.
2. This leads to the idea of making up any unit system
you want. So, if you pick a number 10, for example in the Square for, say, the
aluminum material, you can have this as 10 grams, or 10 kilograms, or 10 mu,
where the units "mu" is just made up and is some conversion factor to
grams. So the number 10 can really mean any "amount".
3. He says you can use any "level" of the
Square for selecting the "amount" of materials to use. This again
seems to be saying you can adjust the number almost arbitrarily.
4. He doesn't provide any sense of (let alone specifying
some precision for) the accuracy in measuring (or machining) the materials.
Because of these short comings, it looks like
you can use almost any "amount" of the materials that you want. That
is, there doesn't seem to be significant constraints on the "amount"
of material to use in the construction of his devices.
The example and calculations provided here
are for illustration purposes only. Searl might use some other Square than the
one I use in this example, but the argument presented here would be the same.
Searl says that to build his SEG devices, you
need to use 4 different materials. These materials are layered into cylinder
shapes and magnetized.
For example, the 4 materials may be aluminum
(conductor), nylon-6 (insulator), iron (ferromagnetic material), and neodymium
(electron source, whatever that's suppose to mean).
As I understand it, Searl says to determine
the "amount" of the 4 different materials to use in constructing his
rings and rollers, you start, for example, with a
Consider the
|
16 |
3 |
2 |
13 |
|
5 |
10 |
11 |
8 |
|
9 |
6 |
7 |
12 |
|
4 |
15 |
14 |
1 |
Next you pick some "level" of the
square to use. For example, if we call the above square a Level 1 square, then
to get a Level 2 square you add 1 to all the numbers. If you want to use a
Level n square, you add (n-1) to each of the numbers in the square. This preserves
the "Magic" Square quality.
Then, in our example, the Level n square
would be
|
n+15 |
n+2 |
n+1 |
n+12 |
|
n+4 |
n+9 |
n+10 |
n+7 |
|
n+8 |
n+5 |
n+6 |
n+11 |
|
n+3 |
n+14 |
n+13 |
n+0 |
It is my understanding that it doesn't really
matter what level of the square that you pick, the device is suppose to still
work.....
The value of the square is then 4n + 30. This
is the sum of any row, column or diagonal.
Now select, for example, the diagonal with
the numbers
n+15;
n+9; n+6; n+0
These are the "amounts" of the 4
materials to use to build the device.
But we have no clue if these numbers are
grams of material, kilograms of material, or cubic centimeters of material,
etc. Searl has said the numbers are the mass of material and at another time he
says it’s the volume of the material. These are very different properties
and leads to very different "amount" of materials.
This also leads to very different ratios of
the materials, depending on the number n. So it’s not a particular blend
of materials that makes it all work. Nor a particular ratio of materials.....
(!!!???)
I also find that it doesn't matter what 4x4
square you start with, nor what row, or column or diagonal as long as you
pick a large n.
If the level doesn't matter then we can
simply pick the ratio of materials to be 25% for each amount of material. That
is, for any Magic Square, as the level is increased, the ratio of the 4
numbers selected will tend toward 25% of the total amount of material.
Again, that's independent of the Magic
Square used.
So, to me, this says the Magic Squares are
irrelevant.
Example: Consider the diagonal mentioned
above with the numbers n+15; n+9; n+6; n+0 for some "level" n > 0.
So, we need n+15 "amount" of material
A, n+9 "amount" for material B, n+6 "amount" for material C
and n+0 "amount" for material D.
Then the total "amount" (whatever
that is) of the materials is
A+B+C+D
= n+15 + n+9 + n+6 + n+0 = 4n+30
Then as n becomes large, the ratios of the
materials with respect to the total amount of material all approach 25%.
The limit as n gets large of A/(A+B+C+D) =
(n+15)/(4n+30)
tends to n/4n = 1/4 which is 25%.
The limit as n gets large of B/(A+B+C+D) =
(n+9)/(4n+30)
tends to n/4n = 1/4 which is 25%.
And similarly for material amounts C and D.
The ratios simply go to 25%.
Here is a graph of these ratios.
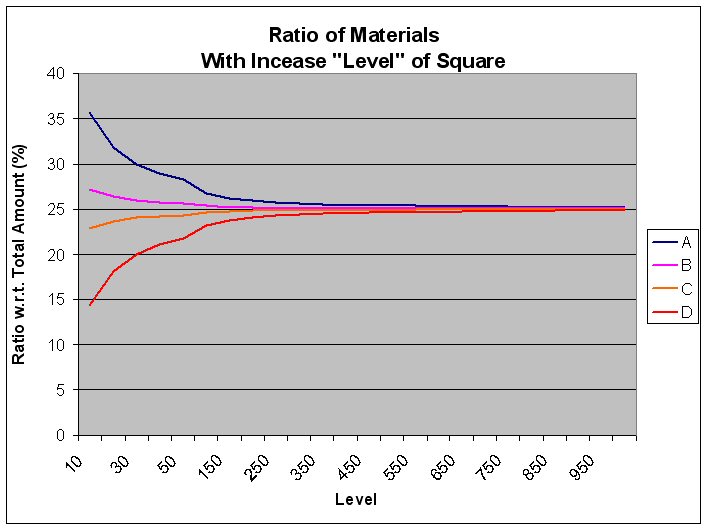
And this is independent of the Magic Square
you started with!
So what's so special about using Searl's Law
of Squares?
Usage Note: My work is copyrighted. You may
use my work with proper acknowledgement but you may not include my work,
or parts of it, in any for-profit project without my consent.
Last updated: 07-07-2006