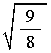
I have been asked to clarify Fuller's Synergetic Constant
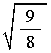
By "Tetrahedron based volume" I mean that the Tetrahedron is defined to be the unit of volumetric measurement, not the Cube.
As I understand it, you need to do 3 things to convert to Synergetics accounting:
1) Identify where in the polyhedron the Tetrahedron edge occurs. If the cube based
volume equation uses a different length than where the Tetrahedron edge occurs in the polyhedron,
then convert the cube base volume equation to use the Tetrahedron edge length.
For the Platonic polyhedra, the Cube is the only polyhedron for which this applies.
2) Multiply by the conversion factor sqrt(9/8), and
3) Take into account the fact that Synergetics counts the unit edge length of the
Tetrahedron to
be 2 sphere radii (sphere diameter) in length. "Unity is plural and at minimum 2".
The (Cube based) equation for the volume of the Tetrahedron is
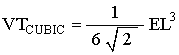
where EL is the edge of the Tetrahedron.
The Tetrahedron edge is used in the cube based volume equation, so we don't need to do anything for step #1.
So, by step #2, and #3, the Volume equation for the Tetrahedron becomes
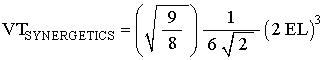
This gives
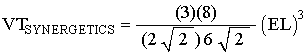
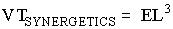
which is the correct Tetrahedron volume equation in Synergetics.
The cubic volume equation for the Icosahedron is
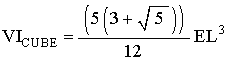
In Synergetics, the Icosahedron edge is associated with the Tetrahedron edge, so we do not need to modify the cube based volume equation by step #1.
By step #2, and #3, we get
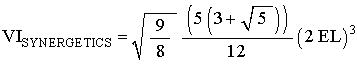
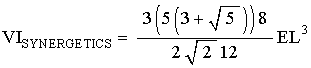
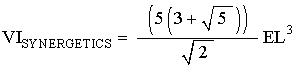
which is the correct tetra-volume equation for the Icosahedron.
The Cube's cube base volume equation is given by:
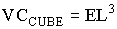
However, in Synergetics, the edge of the Cube is NOT associated with the edge of a Tetrahedron. It is the Cube's face diagonal which is associated with the edge of a Tetrahedron.
So, by step #1, we first, convert EL to the Cube diagonal. (The Cube diagonal corresponds to the Tetrahedron's edge.)
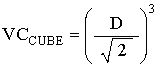
Now that we have the Cube volume equation in terms of the Cube's diagonal, which is a Tetrahedron edge, we continue to convert to Synergetics accounting by step #2, and #3 above:
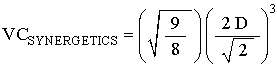
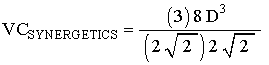
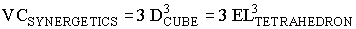
which is the correct Tetrahedron volume equation for the Cube.
For the Octahedron, the cube based volume equation is
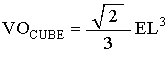
The edge of the Octahedron is associated with the edge of a Tetrahedron, so step #1 does not change the equation.
Applying steps #2 and #3, we get
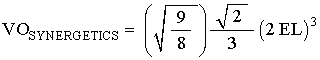
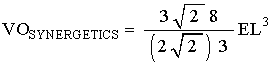

which is the correct tetra-volume volume equation for the Octahedron.
For the regular Dodecahedron, the edge of the Dodecahedron is associated with a Tetrahedron edge. So step #1 does not change the volume equation.
Applying steps #2, and #3, we get
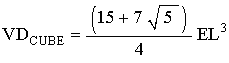
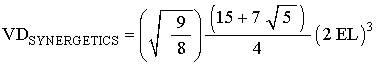
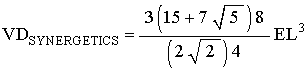
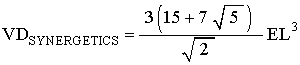
which is the correct tetra-volume for the Dodecahedron.
Note that it is not clear, to me, why the edge of the Icosahedron and the regular Dodecahedron can be associated with a Tetrhadron edge. In particular, the Tetrhahedron occurs within the Dodecahedron but the Tetrahedon edges do not correspond with the edges of the Dodecahedron.
We will explore this "problem" on another web page in the near future.
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.