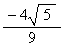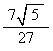We want to prove that the cylinder axis of the Tetrahelix passes through the Tetrahedron’s triangle face at triangle face coordinate (7, 3). 

The radius of the Tetrahelix cylinder is given by

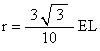
where EL is the edge length of the Tetrahedra making up the Tetrahelix.

The Tetrahelix can be positioned so that its (x, y, z) coordinates are given by the equation

where (approximately 131.8103149 degrees) and

Using the equations

it is easy to calculate values for  and .

n
0	1	0
1
2
3

The n-th Terahelix vertex will then have the coordinate

For the “first” 4 vertices, with EL=1, we get

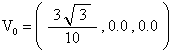
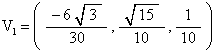
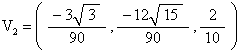
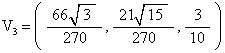
What (7, 3) means is that we travel 7 (out of 10) units along one edge and then 3 units (out of 10) parallel to another edge of the triangular face.

Define V_a to be the vector from vertex V₀ toward vertex V₁ but which is only 7 (out of 10) units in length.  Then define V_b to be the vector from vertex V₁ toward vertex V₂ and which is 3 (out of 10) units in length. 

Then the vector to (one of) the face  point (7, 3) is given by V0 + Va + Vb.   If this vector has no x or y components then it must lay on the z-axis, which is the symmetry axis of the Tetrahelix.

We calculate V_a to be

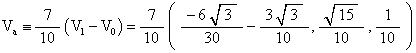
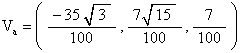
And we calculate V_b to be

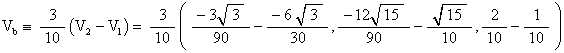
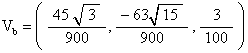
Then the vector to the point face coordinate point (7, 3) is given by

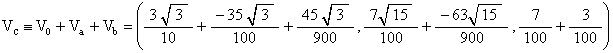
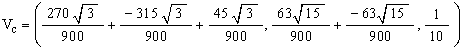
This lays on the z-axis.  So the symmetry axis of the Tetrahelix does pass through the triangular face coordinate (7,3).

There are 3 such face points depending on which of the 3 vertices of the triangular face is used to begin measuring the 7 (and then 3) units of length.

Home Page

rwgray@rwgrayprojects.com