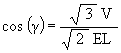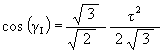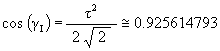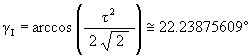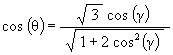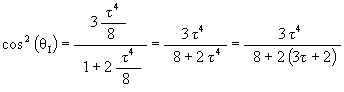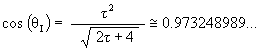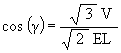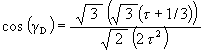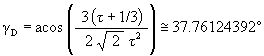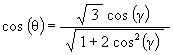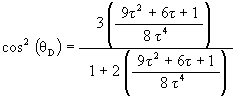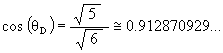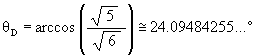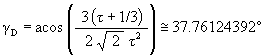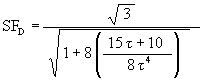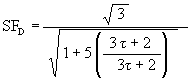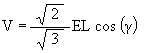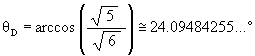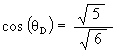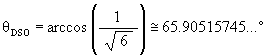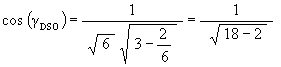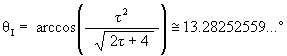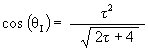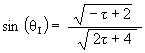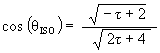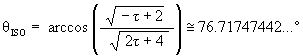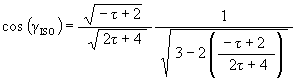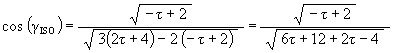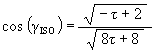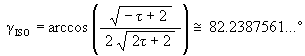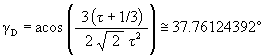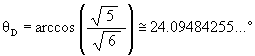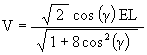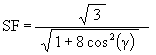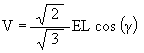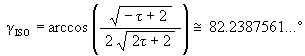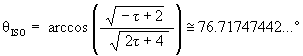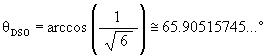For a PDF version of this paper, click on this sentence.

 

 

 

 

The Jitterbug Motion

 

 

By

 

Robert W. Gray

180-4 Poplar St.

Rochester, NY 14620

rwgray@rwgrayprojects.com

 

Copyright, September 2002

 

 

09-29-2002

 

Introduction

 

 

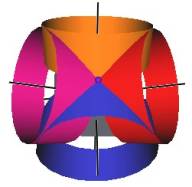
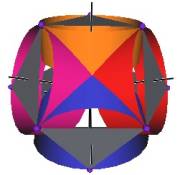
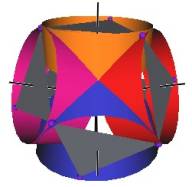
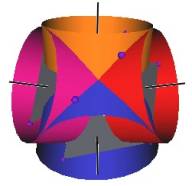
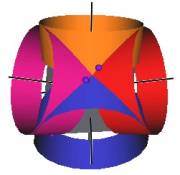
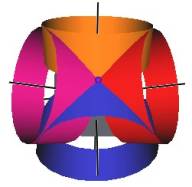
We develop a set of equations which describes the motion of a triangle and a vertex of the Jitterbug.  The Jitterbug starts in the “opened” position of a Cuboctahedron (also called the Vector Equilibrium or VE) with 8 triangle faces, 6 square faces, and 12 vertices, and  “closes” into an Octahedron position with 8 triangle faces and 6 vertices.  (See Figure #1.) 

 

The Jitterbug motion is visually complex but simple when you focus only on the motion of one of the 8 triangles.    The motion of a triangle is simply a radial displacement plus a rotation around the radial displacement vector.  Because the triangular faces do not change size as they move radially and rotate, the 3 vertices of a triangle are always on the surface of a cylinder.  (See Figure #2.)  The cylinder is axially aligned with the displacement vector.  That is, with a line passing through the Octahedron’s (and VE’s) center of volume out through the triangle’s face center point.  There are 4 axes of rotation (two opposite triangular faces per axis) so there are 4 fixed cylinders within which the triangles move.

 

The reason that the motion appears complex is because the Jitterbug is often demonstrated by holding the “top” and “bottom” triangles fixed while pumping the model.  This causes the remaining 6 triangles to move radially in and out, rotate and orbit about the “up” and “down” pumping axis.  By allowing all 8 triangles to move in the same way, that is, not fixing any of the 8 triangles, the motion is simplified.

 

 

 

 

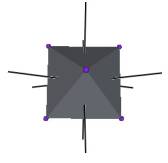
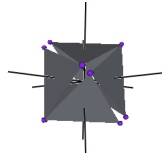
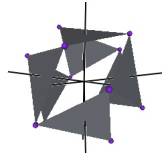
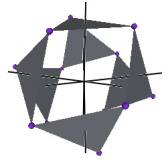
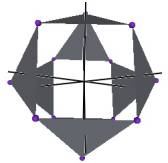
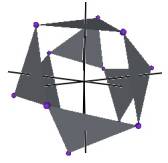
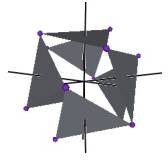
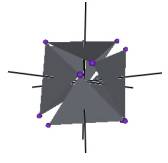
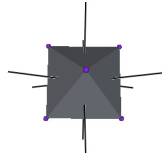
Figure #1 Jitterbug Motion

 

 

 

 

 

 

Figure #2 Jitterbug Motion within cylinders.

 

Development of Vertex Motion Equations

 

 

We first note that since the 8 triangles of the Jitterbug during its motion do not change size, and since they move radially as they rotate, the 3 vertices of any of the 8 triangles are constrained to move on the surface of a cylinder.

 

Second, from the symmetry of the Octahedron and the Jitterbug, each of the vertices of the Jitterbug is constrained to move in a plane.  This can be seen in Figure #2. 

 

Thirdly, a plane cutting through a cylinder defines an ellipse.  

 

Therefore, each of the vertices of the Jitterbug traverses a portion of an ellipse. 

 

Figure #3 Path of a vertex

 

In Figure #3 we can see a portion of this ellipse as well as one triangle of the Jitterbug in the Octahedron and the VE position.   The ellipse shown is in the YZ-plane.  The surrounding cylinder is along the V-axis.

 

Note that since the Octahedron is centered at (0, 0, 0) then so too is the ellipse.

 

The equation of an ellipse, centered at the coordinate origin (0, 0, 0), is given by

           

where a = semimajor axis length and b = semiminor axis length.

Figure #4 Semimajor and semiminor axes lengths

 

From Figure #3, we see that the semimajor axis length, from the coordinate origin to the vertex of the VE positioned triangle, is the edge length of the Tetrahedron (and of the VE) defined by the VE triangle and the center of volume.  This length is given by

            a = EL

Note that since the ellipse is defined on the surface of the cylinder, then the ellipse width must match the cylinder diameter.  This means that the semiminor axis length is just the radius of the cylinder, which is the distance from the face center of a triangle to its vertex

We can now write the equation for the ellipse which a vertex of the Jitterbug will follow.

(1)       

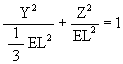
where EL is the edge length of the Octahedron, which is also the edge length of the VE.

 

The eccentricity of an ellipse is defined by the equation

           

Using the above values for a and b:

a = EL

            we get

            b2 / a2 = (1/3) / 1 = 1/3

so that

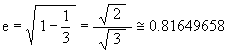
The coordinates for the 2 focus points are (0, ae) and (0, –ae) in the YZ-plane.  These evaluate to

 

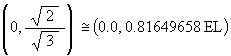
and 

 

 

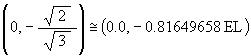
The usual motion of the Jitterbug consists of the vertices moving from the Octahedron to the VE position and back to the Octahedron position.  Then only a portion of the ellipse is traversed by the vertices.

Figure #5 Jitterbug portion of ellipse

 

Figure #6 Orientation of the axes

 

Figure #6 shows the various axes and their orientations used in the following derivations.

 

It is important to note that there are two axes of rotations used in the derivations.  The first axis is the V-axis shown in Figure #3 and Figure #6.  It is the axis about which the Jitterbug triangle rotates.  The second axis is the X-axis of Figure #6 and Figure #7.  The X-axis rotates the ellipse radius (labeled “r” in Figure #7) around the ellipse.    It is important to note that an angular of rotation g about the V-axis does not equal the same angular amount of rotation q about the X-axis.

g ¹ q

 

Figure #7 Orientation of ellipse and cylinder

 

We will shortly derive relations which will let us convert a Jitterbug’s triangle angular rotation g from the ellipse radius sweep angle q and visa versa.

 

(Note that I am using the term ellipse “radius” very loosely here.  The ellipse does not have a radius.  However, the word “radius” makes it easy to refer to a line segments with one end at the coordinate origin and the other end on the perimeter of the ellipse.)

 

Considering Figure #7, we have defined the ellipse to be in the YZ-plane.  The cylinder has its axial symmetry axis along the V axis and the W axis of the cylinder is perpendicular to the V and to the Y axes.  The left side of Figure #7 is rotated about the Z axis to get the right side of the Figure.

 

Note that both coordinate systems (X, Y, Z) and (W, Y, V) share the same Y-axis.

 

We now want to calculate the Z and Y component of the  ellipse radius r, which has been rotated by the angular amount q about the X-axis (so it remains in the YZ-plane.)

 

From the ellipse equation above, we can write

(2)        3Y2 + Z2 = EL2

We note that

            r2 = Y2 + Z2

and that

            r cos(q) = Z

so

            r2 = Z2 / cos2(q)

This gives the equation

            Y2 + Z2 = Z2 / cos2(q)

            Y2 = Z2 / cos2(q) - Z2

Using this in equation (2) and solving for Z2, we get

3Z2 / cos2(q) - 3Z2 + Z2 = EL2   

 

 

Using  this equation and equation (2), we can solve for Y

 

We need a relation relating q to g which is the angular amount a triangle is rotated about the V-axis.

 

The angle which the YZ-plane makes with the V axis  is labeled a in Figure #3.  This is the half-cone angle of the Tetrahedron in the VE.   This angle is known to be

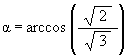
which makes the angle b  (see Figure #3)

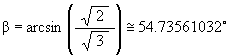
We then have

           

           

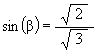
Now,

W = Z cos(b)

Using this in equation (2) we get

(2)        3Y2 + Z2 = EL2

            Y2 = (1/3)EL2 – W2 

With

            tan(g) = Y/W 

so that

tan2(g) = Y2/W2 

 we get

           

 

 

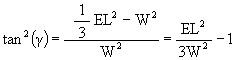
We can use a trigonometric identity

tan2(A) = (1/cos2(A)) – 1

to rewrite this as

(1 / cos2(g)) – 1 = 3( (1 / cos2(q)) – 1 )

(1 / cos2(g)) – 1 = (3 / cos2(q)) – 3

1 / cos2(g) = (3 / cos2(q)) – 2

1 / cos2(g) = (3 / cos2(q)) – 2 cos2(q) / cos2(q)

1 / cos2(g) = (3 – 2 cos2(q)) / cos2(q)

            cos2(g) = cos2(q) / (3 – 2 cos2(q))

           

Solving for cos(q), we get

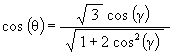
We can then write Z as a function of the Jitterbug rotation angle g

 

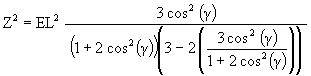
We now calculate the position of the Jitterbug triangle along the V-axis.  This is the axis around which a single triangle rotates and moves radially.

 

From Figure #7 we have

            V = Z sin(b)

Which means

(3)       

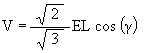
This equation gives the distance that the Jitterbug triangle is from the center of volume as it rotates around the V-axis.  The angular range is – 60° £ g £ 60°, with g = – 60° is one Octahedron position, g = 0° is the VE position and g = 60° is the other Octahedron position.

 

 

 

The Jitterbug Ellipses

 

In Figure #8, the “Jitterbug portion” is the actual path that vertices will travel (direction of travel is not considered here.)  No vertex of the Jitterbug (when considering only the Octahedron to VE to Octahedron motion) traverses that portion of the ellipse curve which is within the “Square cross section of Octahedron” portion of the ellipse. (See Figure #8.)   Later in this paper we will consider what happens if the vertices are allowed to move around the complete ellipse.

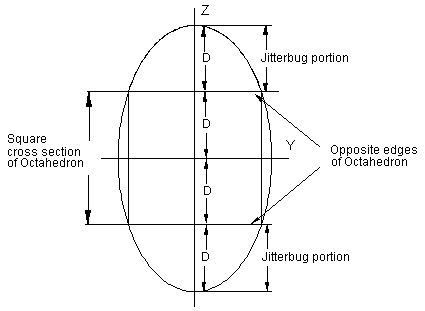
Figure #8 Ellipse and Octahedron edges

 

Figure #8 shows the complete ellipse in the YZ-plane with the usual Jitterbug vertex path portion of the ellipse marked.   In the following sections of this paper we will explore the consequences of allowing the vertices of the Jitterbug to orbit around the entire ellipse.

 

Note that there are 2 diametrically opposite Jitterbug vertices per ellipse which travel in the same direction.   So there are two “Jitterbug portions” to the ellipse.  Since there are 12 vertices to the Jitterbug (not in the Octahedron position) then there are 12/2 = 6 total ellipses for the Jitterbug.

 

Note that the angular range traversed by a vertex along the ellipse in the YZ-plane is

– 45° £ q £ 45°

 

All four of the square’s edges in the ellipse of Figure #8 are Octahedron edges.  Each pair of opposite edges of the Octahedron is part of an ellipse.  Therefore, there are two orthogonal ellipses in the same plane.   Figure #9 shows both ellipses defined by the motion of 4 Jitterbug vertices. 

 

 

Figure #9  Two ellipse per plane

 

Following only one vertex (one vertex of a rotating Jitterbug triangle) and with the Jitterbug in the Octahedron position, we label the initial vertex position “P1” .  This vertex will travel along the ellipse, passing through an Icosahedron position, to reach vertex position “P2”, the VE vertex position.  Then, with the Jitterbug triangle continuing to rotate in the same direction, the Jitterbug vertex passes through another Icosahedron vertex position to reach the Octahedron position “P3”.  (Further details relating the Jitterbug vertex position along the ellipse and various polyhedra are given below.)  Note that if the Jitterbug triangles were allowed to continue to rotate in the same direction then the vertex now at vertex position “P3” would not proceed to vertex position “P4”. Instead, is leaves this plane to follow another ellipse.

 

The Octahedron has 12 edges forming 6 opposite edge pairs.  So there are a total of 6 ellipses to define the complete Jitterbug motion.  These 6 ellipses are show in Figure #10 and Figure #11.

 

Figure #10 Six ellipses and Octahedron

 

Figure #11 Six ellipses and the VE

 

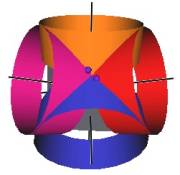
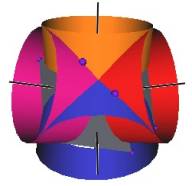
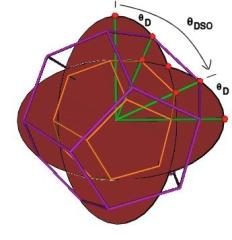
It is well known, and as mentioned above, that the Jitterbug vertices pass through an Icosahedron position during its Jitterbug motion.  (See Figure #12.)  What is not well know is that the Jitterbug vertices also pass through a regular Dodecahedron position along the ellipses.  (See Figure #13.)

 

 

Figure #12 Jitterbug in Icosahedron position

Figure #13 Jitterbug in regular Dodecahedron position

Unlike the Jitterbug in the Icosahedron position, not all the vertices of the regular Dodecahedron are defined by one Jitterbug.  The Dodecahedron has 20 vertices.  The Jitterbug in the Dodecahedron position (as well as in the Icosahedron position) has only 12 vertices.  To completely define all 20 vertices of the Dodecahedron in a symmetrical way requires 5 Jitterbugs.  This gives a total of 5 ´ 12 = 60 vertices.  When this is done, the pentagon faces of the Dodecahedron become pentagrams.  (It is possible to cover all the Dodecahedron vertices with 3 Jitterbugs but not in a symmetrical way.  That is, not in a way as to have each of the Dodecahedron’s vertices covered by the same number of Jitterbug vertices and each of the Dodecahedron’s faces containing the same number of Jitterbug triangle edges.)

 

Figure #14 Symmetrical covering of Dodecahedron by 5 Jitterbugs

 

(These 5 Jitterbugs are the basis for the 120 Polyhedron as explained in the paper “What’s in this Polyhedron?” which can be found at http://www.rwgrayprojects.com/Lynn/NCH/whatpoly.html)

 

The Jitterbug in the VE position is shown in Figure #15.

 

Figure #15 Jitterbug in the VE position

 

Because of the symmetry of the elliptical path about its semimajor axis, a Jitterbug vertex will pass through 2 Icosahedra and 2 regular Dodecahedra positions.   These are shown in Figure #16.  The vertex positions labeled “D,C,T”  stand for the “Dodecahedron, Cube, Tetrahedron” position.  (It is well known that 5 Cubes and 10 Tetrahedra share the same vertices as a regular Dodecahedron.)  The positions labeled “O” are the Octahedron positions, those labeled “I” are the Icosahedron positions, and those labeled “VE” are the VE positions.

 

Figure #16 Polyhedra positions of the Jitterbug motion

 

 

 

 

 

 

 

 

We can calculate the angular amount g that the Jitterbug triangle rotates from the VE (g=0°) position into the Icosahedron position (gI).

 

Starting with equation (3)

(3)       

we write

(4)       

 

Now, the distance from the center of volume to the face center of an Icosahedron’s triangle face is

 

where

 

Here, we have V = DVFI for equation (4).

 

Since the size of the Icosahedron triangles are the same as the size of the Jitterbug triangles, we have

ELI = EL

Then equation (4) for the Icosahedron position of the Jitterbug becomes

           

Which gives gI  @ 22.23875609°.

This means that the Jitterbug triangle is rotated by the angular amount

from the VE position (clockwise or counter clockwise) to be in the Icosahedron position.

 

Note that the triangles of the Jitterbug are like gears in that if a triangle is rotated clockwise, then the 3 triangles attached to it must rotate counterclockwise.

 

The corresponding angle in the YZ-plane through which the ellipse radius r must sweep through to get to the Icosahedron position can be obtained by using the equation (derived above)

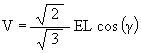
So,

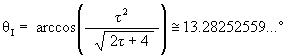
which is the angle about the X-axis that the ellipse radius rotates to the Icosahedron position.

           

To calculate the angular rotation of the Jitterbug triangles for the regular Dodecahedron position, we first find the radial position of one of the Jitterbug’s triangles when in the Dodecahedron position. 

 

Figure #17 Three vertices of the Jitterbug and Dodecahedron

 

Figure #17 shows 3 of the Jitterbug’s vertices coinciding with 3 of the Dodecahedron’s vertices.  It can be shown that these three vertices can be given the (x, y, z) coordinates

            V1 = (0, - t ,  t 3 )

V2 = (- t 3, 0, t)

            V3 = (- t , - t 3, 0)

where . 

 

Using these coordinates sets the Octahedron’s edge length.  In this case, the edge length of the Octahedron, calculated using the equation

            t n+1 = t n  + t n-1  

is

            ELO = distance(V1, V2) = sqrt(t 6 + t 2 + (t 3 - t ) 2  )

            ELO = 2 t 2

Then, using t 3 = t 2 + t  = t  + 1 + t =  2t + 1, the center of the triangle face is at

            FC = (- (t + 1/3),  - (t + 1/3),  (t + 1/3) )

which is a distance

             

from the center of volume.

 

Again, using equation (4)

(4)       

with V = DVFDT and EL = ELO, we get

so that

           

This is the angular amount that the Jitterbug triangle is rotated about the V-axis from the VE position to the Dodecahedron position.

 

To get the angular amount the ellipse radius is rotated about the X-axis to get to the Dodecahedron position along the ellipse, we again use the equation

With

we get

 

 

So, the rotation about the X-axis which sweeps the ellipse radius to the Dodecahedron position is

 

 

Sub-Octahedron Zone

 

As mentioned above, with physical, solid triangles, a Jitterbug’s vertex does not follow the complete path of an ellipse.   We now remove this constraint and let the vertices travel along the complete elliptical path.  There are then two alternatives for Jitterbug triangle motion:

1)      When the Jitterbug triangle reaches the Octahedron position (from the VE position) they continue to rotate in the same direction, reverse their radial direction of motion, and change size as the vertices traverse the sub-Octahedron zone of one of the 6 ellipses,

2)      When the Jitterbug triangle reaches the Octahedron position (from the VE position) they continue to rotate in the same direction, continue to move in the same radial direction (toward the center of volume), and do not change size.

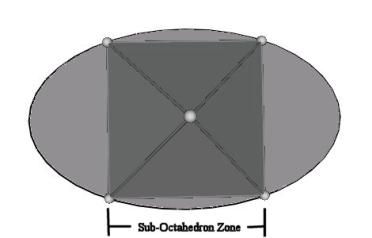
Figure #18 The sub-Octahedron Zone of ellipse

 

We consider the first case here.  In the next section we consider the second case.

 

Beginning in the Octahedron position, the vertices are now to travel within the sub-Octahedron zone of the 6 ellipses of the Jitterbug.  As shown in Figure #19, each of the Octahedron’s vertices split into 2 vertices and the diametrically opposite vertices, on the same ellipse, travel in the same direction. 

 

 

Figure #19 Jitterbug through sub-Octahedron zone

 

Figure #18 Triangle vertices switch ellipses

 

Note that the 3 vertices of a triangle have switched ellipses.  That is, in going from the original VE position to the original Octahedron position, a vertex of a triangle follows a particular ellipse.  For the triangle to continue to rotate and to remain on some elliptical path,  the vertex of the triangle switches to one of the other 3 ellipses which pass through the same Octahedron vertex position.  The vertex, having switched, can now travel along the sub-Octahedron zone portion of an ellipse. 

 

Figure #20 shows one triangle of the Jitterbug’s triangles with its 3 vertices on ellipses 1, 3, and 6.  Once the triangle is in the Octahedron position, the vertices switch to follow along ellipses 5, 2, 4, respectively.

 

In order to accomplish this motion, the Jitterbug triangles move radially, rotate and change scale.  This scale change is unlike the motion of the original Jitterbug motion describe previously.

 

In one sub-Octahedron zone position it is seen that the Jitterbug forms another, smaller VE.  (See Figure #19.)  Being another VE configuration, we can draw another pair of smaller ellipses within the original ellipses.  This construction of another sub-VE  within the original VE by following the ellipse paths can be continued to form sub-sub-VEs, etc. and therefore sub-sub-Jitterbugs.

Figure #21 First sub-Jitterbug ellipses

 

As Figure #21 shows, the Octahedron vertex at P1 is moved to position P2 along the sub-Octahedron zone of the original ellipse.  Again, this is not part of the normal Jitterbug  motion and is accomplished by a continuous change in scale of the triangles.  From P2, a sub-VE position, the vertex may either continue along the original ellipse or it may smoothly switch to the smaller embedded ellipse and move to P3.  P3 is a sub-Octahedron vertex position.  The motion from P2 to P3 is a normal Jitterbug motion, i.e. without scaling.

 

As before, we can map out the various polyhedra positions of the Jitterbug motion as its vertices traverse the sub-Octahedron zone.  This is shown in Figure #22 and Figure #23.

Figure #22 One Dodecahedron, Icosahedron and VE position

within sub-Octahedron Zone of ellipse

 

Figure #23 Dodecahedron, Icosahedron and VE positions

 

From the original, large VE, (maximum radial distance from the center of volume) a triangle will move radially inward and rotate to the original, large Octahedron position.  To then move to the sub-VE position, the triangle must reverse its radial direction (it moves radially outward) rotate (in either the same direction or opposite direction) and change scale (shrink in size.)

 

The path that a vertex will follow in the sub-Octahedron zone of the YZ-plane is just the edge of the original ellipse rotated 90 degrees.  See, for example Figures #19 and #21 which show the 2 ellipses in the same YZ-plane, one rotated 90 degrees to the other.

 

The equation for the rotated ellipse in the YZ-plane is

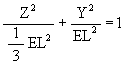
From which we get

            Y2 = EL2 – 3Z2

Now,

            r2 = Y2 + Z2

as well as

            r cos(q) = Z

            r2 = Z2 / cos2(q)

Combining these equations gives

Z2 (1 + 2cos2(q)) = EL2 cos2(q)

To write this in terms of the angular rotation of the Jitterbug triangle g, we again use

 

 

 

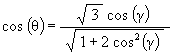
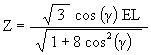
As before, the radial position of the Jitterbug triangle (which moves radially along the V-axis) is given by

V  = Z sin(b)

And since

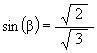
we have

 

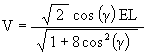
where the angular range is now -60° £ g £ 60° about the V-axis.

 

When the triangle is rotating from the original Octahedron position to the sub-VE position, the scale of the triangle is decreased.  When the triangle further rotates from the sub-VE position to the second Octahedron position, the scale of the triangle increases back to its original size.

 

We now determine an equation for these scale changes.

 

The Scale Factor by which the original sized Jitterbug is reduced is given by the equation

 

where DFV(g) is the Distance from the triangle’s Face center to its Vertex, which is now changing as a function of the angular amount the triangle is rotating g.  DFVO is the original Octahedron’s Distance from the triangle’s Face center to its Vertex.  Since

DFVO = EL / sqrt(3), we have

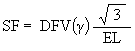
We have

DFV(g)2 = W2 + Y2

Now,

            W = Z cos(b)

and cos(b) = 1 / sqrt(3), so

           

Using Y2 = EL2 – 3Z2 from above, we get

or

The Scale Factor equation then becomes

 

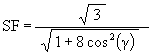
At g = 0°, which is the sub-VE position, the Jitterbug is reduced by a factor of

 

An alternative calculation for the sub-VE position can be calculated by noting  that position P2 is at the semiminor axis position of the larger ellipse and is the semimajor axis position of the smaller ellipse.  Therefore, the Jitterbug in the sub-VE position is reduced by the  scale factor (SF) 

            SFVE =  small ellipse semimajor axis  /  large semimajor axis

      = large ellipse semiminor axis  /  large semimajor axis

       

 

The Scale Factor for the Dodecahedron position of the Jitterbug is now calculated.

 

Recall that the angle of rotation of the Jitterbug triangle for the Dodecahedron position is

so

           

and

Then

It can be shown that t4 = 3t + 2, so we get

 

 

 

Now for the Icosahedron’s scale factor. 

 

We know that the rotation angle for the Icosahedron position is

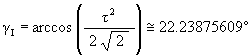
so that

           

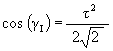
Then

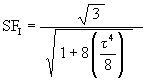
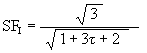
And with t2 = t + 1, we get

            SFI = 1 / t @ 0.618033988….

 

 

Alternative Sub-Octahedron Zone Motion

 

 

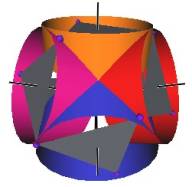
There is another way for the vertices of the original sized Jitterbug to traverse the sub-Octahedron zone portion of the ellipse.  With this alternative method the triangles do not change scale and they continue to move radially inward.  This can be accomplished by allowing the triangles to interpenetrate one another.  See Figure #24.   Note that the triangles’ vertices are still paired.  That is, the triangles are still joined together.

 

As Figure #24 shows, the same sequence of polyhedra (Dodecahedron, Icosahedron, VE) occur as in the previous case.

 

When the vertices are in the VE position, the 8 Jitterbug triangles all have their face centers at the coordinate origin (0, 0, 0).

 

For the vertices of the Jitterbug to traverse the sub-Octahedron zone (starting from the “closed” Octahedron position), the triangles rotate an additional 30 degrees (about the V-axis) to the sub-VE position and another 30 degrees from the sub-VE  to the second original Octahedron position.  From the Octahedron to sub-VE position, the triangles move radially inward a distance of 

which places all 8 triangles of the Jitterbug at the coordinate origin (0,0,0).  From the sub-VE position to the  second original Octahedron position, the triangles have passed through the coordinate origin and have moved outward a distance of DVFO.

 

Note that these rotations are half that of the original Jitterbug motion (the non-sub-Octahedron zone motions) but that the total radial displacement from the original Octahedron to sub-VE  position is the same as the total radial displacement from the original Octahedron to the original VE position.

 

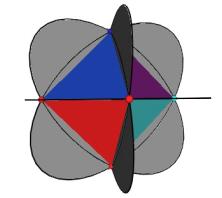
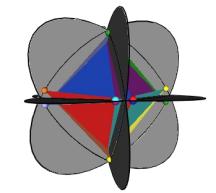
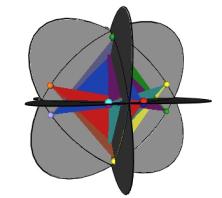
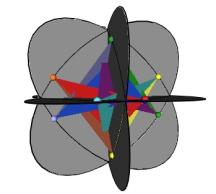
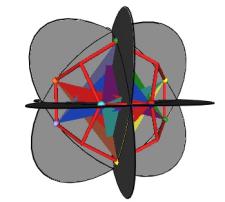
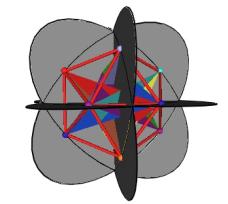
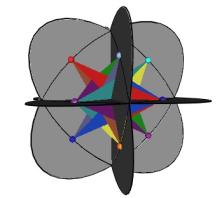
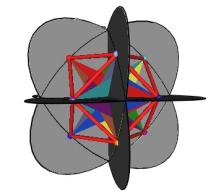
Figure #24 Triangles are allowed to interpenetrate

 

We now develop equations for the vertex motion along the sub-Octahedron zone.

 

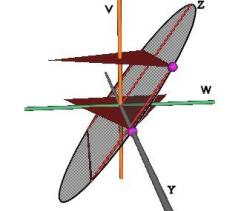
Figure 25 Orientation of ellipse and axes

 

We have already developed the equation for the distance along the V-axis to the location of the Jitterbug triangles.

(3)       

where, for this case the angular range is 60° £ g £ 120° with the Octahedron position occurring at g = 60°, the sub-VE position occurring at g = 90° and the second Octahedron position occurring at g = 120°.   (If the triangle were rotating in the opposite direction then the angular range would be - 60° £ g £ - 120°.)

 

Now, the angular positions of the Dodecahedron and the Icosahedron for the sub-Octahedron zone can be calculated as follows. 

 

Consider the Dodecahedron in Figure #26.  We see that the rotation angle qDSO in the YZ-plane of the ellipse radius to the Dodecahedron position in the sub-Octahedron zone is

qDSO = 90° - qD

 

 

Figure #26 Angle for sub-Octahedron zone Dodecahedron position

 

From the original Jitterbug motion calculations, we know that

so

and

which means

cos(qDSO) = cos(90° - qD) = cos(90°)cos(qD) + sin(90°)sin(qD)

            cos(qDSO) = sin(qD)

Therefore

           

Then, using the equation derived previously,

we get

            cos(gDSO) = 1/4

which means that

            gDSO = arccos(1/4)  @ 75.52248781…°

This is the angular amount the triangle is rotated about the V-axis to be positioned into the first sub-Dodecahedron position along the sub-Octahedron zone of the ellipse.

 

For the Icosahedron position, we know that

which means that

Then with

cos(qISO) = cos(90° - qI) = sin(qI)

we have

Using

we get

 

This is the angular amount that the Jitterbug triangle is rotated about the V-axis to position the triangle’s vertex at the first Icosahedron position along the sub-Octahedron zone of the ellipse.

 

As with the previous case for the vertices traversing the sub-Octahedron zone of the ellipse, the Jitterbug (and polyhedra) is scaled.  The scale factors are the same as previously calculated for the previous case. However, in this case in which the triangles interpenetrate each other as the vertices traverse this portion of the ellipse, the scale of the triangles do not change. 

 

 

 

 

 

 

 

 

 

 

 

Additional Comments

 

 

The Jitterbug ellipse is such that it passes through 6 vertices of the combined odd-even FCC lattices.

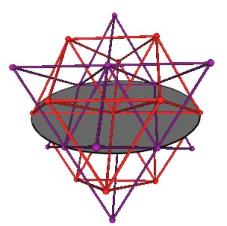
Figure 27 Ellipse in odd-even FCC combined lattice

 

In Figure #27, the red is the even (vertex centered) FCC lattice and the purple is the odd (Octahedron centered) FCC lattice.

 

Two Jitterbugs can not share the same triangular face and have their positions (location of center of volume)  fixed as they go through the Jitterbug motion.  If two Jitterbugs are to share the same triangle face then as the joined  Jitterbugs jitterbug, the positions of the Jitterbugs must move.

 

As Fuller points out, when in the Octahedron position, it is possible to “twist” the Jitterbug  to make it collapse and lay flat.  It can then be folded into a Tetrahedron.

 

There are many Jitterbugs, of various sizes, in the 120 Polyhedron.  The planes of the initial 5 Jitterbugs of the 120 Polyhedron align with the planes of the great circles of polyhedra rotational symmetries which define the 120 spherical triangles on a sphere.

Figure 28 Five Jitterbugs’ ellipse sets in the planes of

15 Great Circles to define a 120 Polyhedron like structure

 

One way to look at an ellipses on the surface of the surrounding cylinder is to recognize that the equation

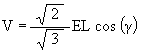
is simply a cosine wave wrapped around the cylinder.  There are 3 such cosine waves wrapped onto the surface of a  Jitterbug cylinder corresponding to the 3 vertices of a Jitterbug triangle.

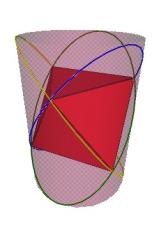
Figure #29  Three Jitterbug ellipses on a cylinder

 

 

 

Summary

 

 

The vertices of the Jitterbug triangles move on elliptical paths.  

There are 6 ellipses per Jitterbug.  These 6 ellipses define 3 planes, 2 ellipses per plane.  The planes intersect each other at 90 degrees.  The 2 ellipses per plane intersect each other at  90 degrees.

For the “normal” Jitterbug motion, based on physical, rigid mechanical models,  the vertices of the Jitterbug do not travel along the complete elliptical path.

 

The equation for the Jitterbug ellipse is

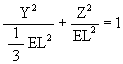
The parametric form of the equation for the ellipse is given by

with 0° £ q £ 360° is the angle of rotation of the ellipse “radius” about the X-axis.

 

The semimajor axis is (EL = the edge length of the Jitterbug)

            a = EL

The semiminor axes is

.

The eccentricity of the ellipse is

.

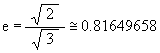The coordinates for the 2 focus points in the (Y, Z) plane are

 

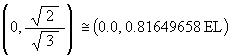
and 

 

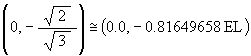
The equations used to convert a rotation of the ellipse radius by the angle q amount about the X-axis to the corresponding rotation of the triangle by the angle g amount about the V-axis and visa versa are

For the “normal” Jitterbug motion, -60° £ g £ 60° with g = -60° being the first Octahedron position, g = 0° being the VE position, and g = 60° being the second Octahedron position.  The corresponding YZ-plane rotation angles of the ellipse radius is -45° £ q £ 45°.

 

The radial position of the Jitterbug triangle with respect to its rotation about the V-axis is given by

 

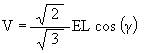
As the Jitterbug moves from the VE position to the Octahedron position, the vertices pass through first an Icosahedron position and then a regular Dodecahedron position.

 

The angular amount that a Jitterbug triangle is rotated (in either direction) from the VE position to the Icosahedron position:

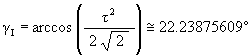
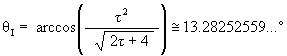
The angular amount that the Jitterbug triangle is rotated (in either direction) from the VE position to the Dodecahedron position:

 

By removing the constraint of fixed sized, impenetrable triangles, the vertices of the Jitterbug  can be made to travel along the “sub-Octahedron Zone” portion of the ellipse.   There are then 2 different ways that the vertices can traverse this part of the ellipse

1)      By allowing the scale of the Jitterbug triangles to change, but still not allowing the triangles to interpenetrate each other,

2)      By allowing the Jitterbug triangles to interpenetrate each other without changing the size (scale) of the triangles.

 

CASE 1:

For this case, the radial distance of the triangles is given by the equation

with -60° £ g £ 60°.

 

The Jitterbug triangles are scaled by the Scale Factor

For the VE position (g = 0°)

For the Dodecahedron position (g = gD above)

           

For the Icosahedron position (g = gI above)

SFI = 1 / t @ 0.618033988….

 

CASE 2:

For this case, the Jitterbug triangles interpenetrate but do not change scale.  However, the corresponding polyhedra do change scale as in case 1 above.

 

The radial position of the triangles is given by

where 60° £ g £ 120° with the Octahedron position occurring at g = 60°, the sub-VE position occurring at g = 90° and the second Octahedron position occurring at g = 120°.   (If the triangle were rotating in the opposite direction then the angular range would be - 60° £ g £ - 120°.)

 

The Icosahedron position is at

 

The sub-Dodecahedron position is at

gDSO = arccos(1/4)  @ 75.52248781…°

The sub-VE position occurs at the angle

            gVESO = 90°

            q VESO = 90°

 

References

 

Fuller, R. Buckminster, Synergetics, MacMillan Publishing Company, 1982

 

The folowing references were not used for writing of this paper.  They were discovered only after I had done my own calculations and illustrations for this paper. 

 

Angell, I. O. and Moore, M. "Symmetrical Intersections of Cylinders." Acta Cryst. Sect. A 43, 244-250, 1987.

Moore, M. "Symmetrical Intersections of Right Circular Cylinders." Math. Gaz. 58, 181-185, 1974.