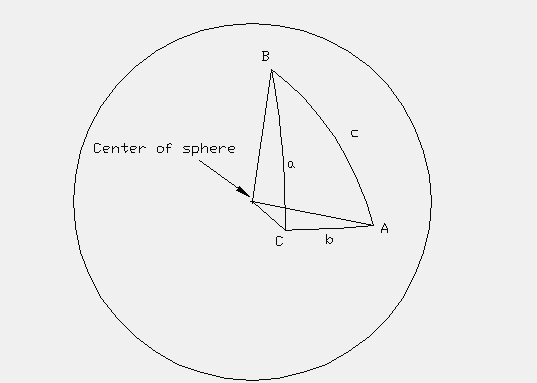
I used spherical trigonometry to calculate all the angles for the 48 and the 120 LCD spherical triangles of the vector equilibrium and the icosahedron generated by the primary great circles. The presentation given here is far from complete and provides no proofs of the relations stated.
The only text book on spherical trigonometry which I have been able to locate is Plane And Spherical Trigonometry, by Kells, Kern, and Bland, McGraw-Hill Book Co., 1940. Other sources to consult are mathematics encyclopedia and dictionaries.
A spherical triangle is defined when three planes pass through the surface of a sphere and through the sphere's center of volume.
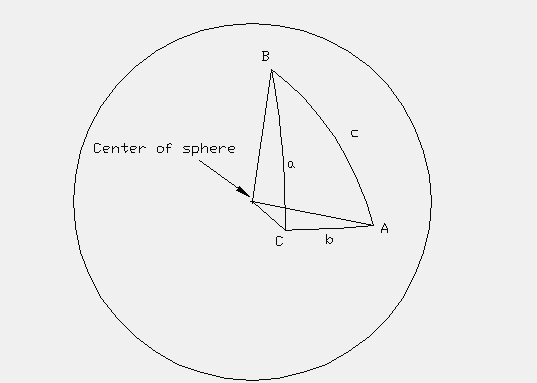
As with plane trigonometry, it is usually easiest to work with a right
spherical triangle. That is, a spherical triangle which has a
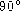surface angle. I will label this
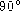surface angle with the capital
letter 'C'. This means that the planes which define angle 'C' intersect each
other at 
.
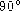It may be necessary to either extend a spherical triangle or divide a spherical
triangle into two triangles in order to obtain a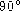 
spherical
triangle. See below. This is often done in plane trigonometry.
Let B be an angle. We define the complement angl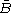e 
to be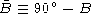 
. Then from the trigonometric relations given in
Plane Trig, we have
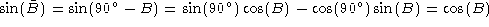
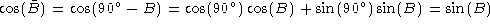
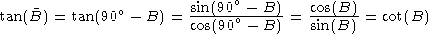
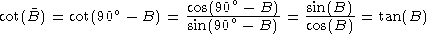
Note that in paragraph 1050.40 of Synergetics, the complement angle, identified
by a small superscript 'c', is incorrectly identified as being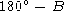 
. The angle 
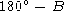is known as the supplemental angle.
Napier's Rules for a spherical right triangle may be stated as:
1. The sine of an angle is equal to the product of cosines of the opposite two angles.
2. The sine of an angle is equal to the product of tangents of the two adjacent angles.
There is an easy way to determine which angles are the opposite and which
angles are the adjacent angles. Consider the spherical right triangle
in which the surface angle C is
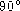. We may write the 5
other angles (the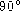 
surface angle is omitted) into a circle which has
been divided into 5 ''pieces of pie''.
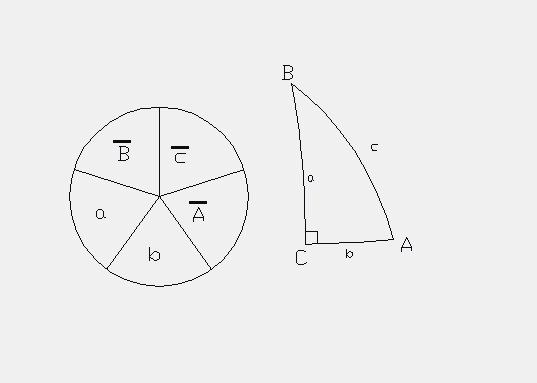
For example, starting with the angle b
and moving in a counter clockwise direction around the spherical triangle, the
angles b, a, B, c, and A
are enter into the circle also in a counter
clockwise direction. We must now take the complement of all the angles which
are NOT connected to the 
surface angle C. These angles are B,
c, and A and are the angles connected to the hypotenuse. So, a bar is
written over these three angles in the circle to give us
,
,
and 
.
It is now easy to see which angles are opposite and which angles
are adjacent. For example, pick angle a. The Napier circle shows that
the two opposite angles are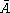 
and 
while the two adjacent angles
are b and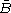 
. Therefore, from Napier's Rule #1 (and the above
relations for complimentary angles), we have
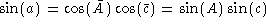
and from Napier's Rule #2, we have
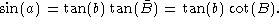
The following relations hold for spherical triangles other than just the spherical right triangle.
The Law of Cosines (central angles):
1. cos(a) = cos(b)cos(c) + sin(b)sin(c)cos(A)
2. cos(b) = cos(a)cos(c) + sin(a)sin(c)cos(B)
3. cos(c) = cos(a)cos(b) + sin(a)sin(b)cos(C)
The Law of Cosines (surface angles):
1. cos (A) = - cos(B)cos(C) + sin(B)sin(C)cos(a)
2. cos (B) = - cos(A)cos(C) + sin(A)sin(C)cos(b)
3. cos (C) = - cos(A)cos(B) + sin(A)sin(B)cos(c)
The Law of Sines:
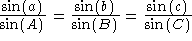
If we know the angles a, A, and b, then we can solve for the angle B by the Law of Sines
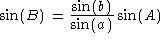
It is possible when using the Law of Sines to obtain no solution, one solution,
or two solutions. In the above example, if
,
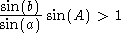then the Law of Sines gives no information about angle B since the sine
of an angle is always less than or equal to one. We must also remember that
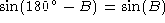and so we must consider not only the angle
B but also its supplement 
.
So there are two possible
solutions, B and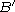 
.
One of the solutions can be discarded if we know some
other constraint on the angle B. For example, if we know that
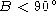and the Law of Sines gives us
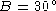and
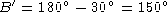, we
can discard the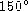 
solution.
Although there are other relations which could be stated, these are the only ones which I have needed in order to calculate the spherical triangle data in the Synergetics books.
There are many methods for obtaining the solution to a spherical trigonometry problem as well as many other details which you will find in a spherical trigonometry text book.
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.