 |
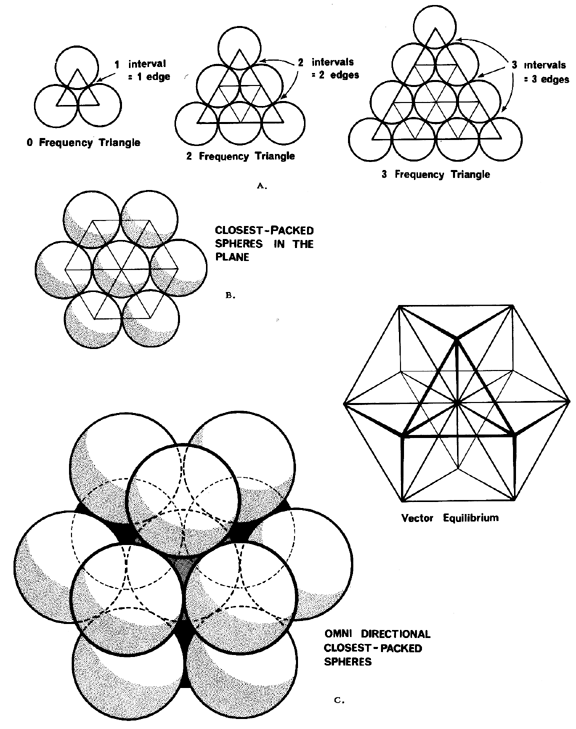
| Fig. 413.01 Vector Equilibrium: Omnidirectional Closest Packing Around a Nucleus: Triangles can be subdivided into greater and greater numbers of similar units. The number of modular subdivisions along any edge can be referred to as the frequency of a given triangle. In triangular grid each vertex may be expanded to become a circle or sphere showing the inherent relationship between closest packed spheres and triangulation. The frequency of triangular arrays of spheres in the plane is determined by counting the number of intervals (A) rather than the number of spheres on a given edge. In the case of concentric packings or spheres around a nucleus the frequency of a given system can either be the edge subdivision or the number of concentric shells or layers. Concentric packings in the plane give rise to hexagonal arrays (B) and omnidirectional closest packing of equal spheres around a nucleus (C) gives rise to the vector equilibrium (D). |