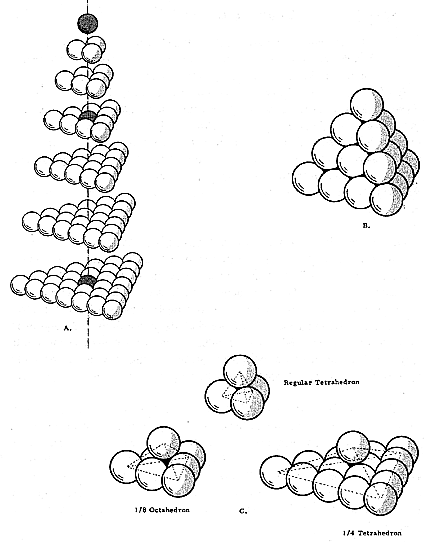
Fig. 415.55 Tetrahedral Closest Packing of Spheres:
Nucleus and Nestable Configurations:
- In any number of successive planar layers of tetrahedrally
organized sphere packings, every third
triangular layer has a sphere at its centroid (a nucleus).
The 36-sphere tetrahedron with five spheres
on an edge (four-frequency tetrahedron) is the lowest
frequency tetrahedron system which has a
central sphere or nucleus.
- The three-frequency tetrahedron is the highest frequency
without a nucleus sphere.
- Basic "nestable" possibilities show how the regular
tetrahedron, the 1/4-tetrahedron and the 1/8-
octahedron may be defined with sets of closest packed
spheres. Note that this "nesting" is only
possible on triangular arrays which have no sphere at
their respective centroids.
|