
 Tetrahedral Precession of Closest-Packed Spheres
Tetrahedral Precession of Closest-Packed Spheres

|
416.00  Tetrahedral Precession of Closest-Packed Spheres
Tetrahedral Precession of Closest-Packed Spheres
|
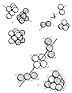 Fig. 416.01 |
416.01
 You will find, if you take two separate parallel sets
of two tangent
equiradius spheres and rotate the tangential axis of
one pair one-quarter of a full circle,
and then address this pair to the other pair in such
a manner as to bring their respective
intertangency valleys together, that the four now form
a tetrahedron. (See Fig. B,
illustration 416.01.)
You will find, if you take two separate parallel sets
of two tangent
equiradius spheres and rotate the tangential axis of
one pair one-quarter of a full circle,
and then address this pair to the other pair in such
a manner as to bring their respective
intertangency valleys together, that the four now form
a tetrahedron. (See Fig. B,
illustration 416.01.)
|

|
416.02
 If you next take two triangles, each made of three
balls in closest packing,
and twist one of the triangles 60 degrees around its
center hole axis, the two triangular
groups now may be nested into one another with the three
spheres of one nesting in the
three intersphere tangency valleys of the other. We
now have six spheres in symmetrical
closest packing, and they form the six vertexes of the
octahedron. This twisting of one set
to register it closepackedly with the other, is the
first instance of two pairs internested to
form the tetrahedron, and in the next case of the two
triangles twisted to internestability as
an octahedron, is called interprecessing of one set
by its complementary set.
If you next take two triangles, each made of three
balls in closest packing,
and twist one of the triangles 60 degrees around its
center hole axis, the two triangular
groups now may be nested into one another with the three
spheres of one nesting in the
three intersphere tangency valleys of the other. We
now have six spheres in symmetrical
closest packing, and they form the six vertexes of the
octahedron. This twisting of one set
to register it closepackedly with the other, is the
first instance of two pairs internested to
form the tetrahedron, and in the next case of the two
triangles twisted to internestability as
an octahedron, is called interprecessing of one set
by its complementary set.
|

|
416.03
 Two pairs of two-layer, seven-ball triangular sets
of closestpacked spheres
precess in a 60-degree twist to associate as the cube.
(See Fig. A, illustration 416.01.)
This 14-sphere cube is the minimum cube that may be
stably produced by closest-packed
spheres. While eight spheres temporarily may be tangentially
glued into a cubical array
with six square hole facades, they are not triangulated;
ergo, are unstructured; ergo, as a
cube are utterly unstable and will collapse; ergo, no
eight-ball cube can be included in a
structural hierarchy.
Two pairs of two-layer, seven-ball triangular sets
of closestpacked spheres
precess in a 60-degree twist to associate as the cube.
(See Fig. A, illustration 416.01.)
This 14-sphere cube is the minimum cube that may be
stably produced by closest-packed
spheres. While eight spheres temporarily may be tangentially
glued into a cubical array
with six square hole facades, they are not triangulated;
ergo, are unstructured; ergo, as a
cube are utterly unstable and will collapse; ergo, no
eight-ball cube can be included in a
structural hierarchy.
|

|
416.04
 The two-frequency (three spheres to an edge), two-layer
tetrahedron may
also be formed into a cube through 90-degree interprecessional
effect. (See Fig. A.)
The two-frequency (three spheres to an edge), two-layer
tetrahedron may
also be formed into a cube through 90-degree interprecessional
effect. (See Fig. A.)
|

|
417.00
 Precession of Two Sets of 60 Closest-Packed Spheres
Precession of Two Sets of 60 Closest-Packed Spheres
|
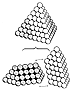 Fig. 417.01 |
417.01
 Two identical sets of 60 spheres in closest packing
precess in 90 degree
action to form a seven-frequency, eight-ball-to-the-edge
tetrahedron with a total of 120
spheres; exactly 100 spheres are on the outer shell,
exactly 20 spheres are in theinner shell,
and there is no sphere at the nucleus. This is the largest
possible double-shelled tetrahedral
aggregation of closest-packed spheres having no nuclear
sphere. As long as it has the 20-
sphere tetrahedron of the inner shell, it will never
acquire a nucleus at any frequency.
Two identical sets of 60 spheres in closest packing
precess in 90 degree
action to form a seven-frequency, eight-ball-to-the-edge
tetrahedron with a total of 120
spheres; exactly 100 spheres are on the outer shell,
exactly 20 spheres are in theinner shell,
and there is no sphere at the nucleus. This is the largest
possible double-shelled tetrahedral
aggregation of closest-packed spheres having no nuclear
sphere. As long as it has the 20-
sphere tetrahedron of the inner shell, it will never
acquire a nucleus at any frequency.
|

|
417.02
 The 120 spheres of this non-nuclear tetrahedron correspond
to the 120 basic
triangles that describe unity on a sphere. They correspond
to the 120 identical right-
spherical triangles that result from symmetrical subdividing
of the 20 identical, equilateral,
equiangular triangles of either the spherical or planar-faceted
icosahedron accomplished by
the most economical connectors from the icosahedron's
12 vertexes to the mid-edges of
the opposite edges of their respective triangles, which
connectors are inherently
perpendicular to the edges and pass through one another
at the equitriangles' center and
divide each of the equilaterals into six similar right
triangles. These 120 triangles constitute
the highest common multiple of system surface division
by a single module unit area, as
these 30º , 60º , 90º
triangles are not further divisible
into identical parts.
The 120 spheres of this non-nuclear tetrahedron correspond
to the 120 basic
triangles that describe unity on a sphere. They correspond
to the 120 identical right-
spherical triangles that result from symmetrical subdividing
of the 20 identical, equilateral,
equiangular triangles of either the spherical or planar-faceted
icosahedron accomplished by
the most economical connectors from the icosahedron's
12 vertexes to the mid-edges of
the opposite edges of their respective triangles, which
connectors are inherently
perpendicular to the edges and pass through one another
at the equitriangles' center and
divide each of the equilaterals into six similar right
triangles. These 120 triangles constitute
the highest common multiple of system surface division
by a single module unit area, as
these 30º , 60º , 90º
triangles are not further divisible
into identical parts.
|

|
417.03
 When we first look at the two unprecessed 60-ball
halves of the 120-sphere
tetrahedron, our eyes tend to be deceived. We tend to
look at them "three-dimensionally,"
i.e., in the terms of exclusively rectilinear and perpendicular
symmetry of potential
associability and closure upon one another. Thus we
do not immediately see how we could
bring two oblong quadrangular facets together with their
long axes crossing one another
at right angles.
When we first look at the two unprecessed 60-ball
halves of the 120-sphere
tetrahedron, our eyes tend to be deceived. We tend to
look at them "three-dimensionally,"
i.e., in the terms of exclusively rectilinear and perpendicular
symmetry of potential
associability and closure upon one another. Thus we
do not immediately see how we could
bring two oblong quadrangular facets together with their
long axes crossing one another
at right angles.
|

|
417.04
 Our sense of exclusively perpendicular approach to
one another precludes
our recognition that in 60-degree (versus 90-degree)
coordination, these two sets precess
in 60-degree angular convergence and not in parallel-edged
congruence. This 60-degree
convergence and divergence of mass-attracted associabilities
is characteristic of the four-
dimensional system.
Our sense of exclusively perpendicular approach to
one another precludes
our recognition that in 60-degree (versus 90-degree)
coordination, these two sets precess
in 60-degree angular convergence and not in parallel-edged
congruence. This 60-degree
convergence and divergence of mass-attracted associabilities
is characteristic of the four-
dimensional system.
|

|
418.00
 Analogy of Closest Packing, Periodic Table, and Atomic
Structure
Analogy of Closest Packing, Periodic Table, and Atomic
Structure
|

|
418.01
 The number of closest-packed spheres in any complete
layer around any
nuclear group of layers always terminates with the digit
2. First layer, 12; second, 42;
third, 92 . . . 162, 252, 362, and so on. The digit
2 is always preceded by a number that
corresponds to the second power of the number of layers
surrounding the nucleus. The
third layer's number of 92 is comprised of the 3 multiplied
by itself (i.e., 3 to the second
power), which is 9, with the digit 2 as a suffix.
The number of closest-packed spheres in any complete
layer around any
nuclear group of layers always terminates with the digit
2. First layer, 12; second, 42;
third, 92 . . . 162, 252, 362, and so on. The digit
2 is always preceded by a number that
corresponds to the second power of the number of layers
surrounding the nucleus. The
third layer's number of 92 is comprised of the 3 multiplied
by itself (i.e., 3 to the second
power), which is 9, with the digit 2 as a suffix.
|

|
418.02
 This third layer is the outermost of the symmetrically
unique, nuclear-system
patterns and may be identified with the 92 unique, selfregenerative,
chemical-element
systems, and with the 92nd such element__ uranium.
This third layer is the outermost of the symmetrically
unique, nuclear-system
patterns and may be identified with the 92 unique, selfregenerative,
chemical-element
systems, and with the 92nd such element__ uranium.
|

|
418.03
 The closest-sphere-packing system's first three layers
of 12, 42, and 92 add
to 146, which is the number of neutrons in uranium__which
has the highest nucleon
population of all the self-regenerative chemical elements;
these 146 neutrons, plus the 92
unengaged mass-attracting protons of the outer layer,
give the predominant uranium of
238 nucleons, from whose outer layer the excess two
of each layer (which functions as a
neutral axis of spin) can be disengaged without distorting
the structural integrity of the
symmetrical aggregate, which leaves the chain-reacting
Uranium 236.
The closest-sphere-packing system's first three layers
of 12, 42, and 92 add
to 146, which is the number of neutrons in uranium__which
has the highest nucleon
population of all the self-regenerative chemical elements;
these 146 neutrons, plus the 92
unengaged mass-attracting protons of the outer layer,
give the predominant uranium of
238 nucleons, from whose outer layer the excess two
of each layer (which functions as a
neutral axis of spin) can be disengaged without distorting
the structural integrity of the
symmetrical aggregate, which leaves the chain-reacting
Uranium 236.
|

|
418.04
 All the first 92 chemical elements are the finitely
comprehensive set of purely
abstract physical principles governing all the fundamental
cases of dynamically
symmetrical, vectorial geometries and their systematically
self-knotting, i.e., precessionally
self-interfered, regenerative, inwardly shunting events.
All the first 92 chemical elements are the finitely
comprehensive set of purely
abstract physical principles governing all the fundamental
cases of dynamically
symmetrical, vectorial geometries and their systematically
self-knotting, i.e., precessionally
self-interfered, regenerative, inwardly shunting events.
|

|
418.05
 The chemical elements are each unique pattern integrities
formed by their
self-knotting, inwardly precessing, periodically synchronized
selfinterferences. Unique
pattern evolvement constitutes elementality. What is
unique about each of the 92 self-
regenerative chemical elements is their nonrepetitive
pattern evolvement, which terminates
with the third layer of 92.
The chemical elements are each unique pattern integrities
formed by their
self-knotting, inwardly precessing, periodically synchronized
selfinterferences. Unique
pattern evolvement constitutes elementality. What is
unique about each of the 92 self-
regenerative chemical elements is their nonrepetitive
pattern evolvement, which terminates
with the third layer of 92.
|

|
418.06
 Independent of their isotopal variations of neutron
content, the 92 self-
regenerative chemical elements belong to the basic inventory
of cosmic absolutes. The
family of prime elements consists of 92 unique sets
of from one to 92 electron-proton
counts inclusive, and no others.
Independent of their isotopal variations of neutron
content, the 92 self-
regenerative chemical elements belong to the basic inventory
of cosmic absolutes. The
family of prime elements consists of 92 unique sets
of from one to 92 electron-proton
counts inclusive, and no others.
|
| Next Section: 419.00 |