700.00 Tensegrity

700.01 Definition: Tensegrity

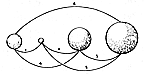
700.011 The word tensegrity is an invention: it is a contraction of tensional integrity. Tensegrity describes a structural-relationship principle in which structural shape is guaranteed by the finitely closed, comprehensively continuous, tensional behaviors of the system and not by the discontinuous and exclusively local compressional member behaviors. Tensegrity provides the ability to yield increasingly without ultimately breaking or coming asunder.
700.02 The integrity of the whole structure is invested in the finitely closed, tensional-embracement network, and the compressions are local islands. Elongated compression tends to deflect and fail. Compressions are disintegrable because they are not atomically solid and can permit energy penetration between their invisibly amassed separate energy entities. As a compression member tends to buckle, the buckling point becomes a leverage fulcrum and the remainder of the compression member above acts as a lever arm, so that it becomes increasingly effective in accelerating the failure by crushing of its first buckled-in side. The leverage-accelerated penetration brings about precessional dispersal at 90 degrees.
700.03 Tension structures arranged by man depend upon his purest initial volition of interpretation of pure principle. Tension is omnidirectionally coherent. Tensegrity is an inherently nonredundant confluence of optimum structural-effort effectiveness factors.
700.04 All structures, properly understood, from the solar system to the atom, are tensegrity structures. Universe is omnitensional integrity.
701.00 Pneumatic Structures
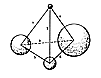
701.01 Tensegrity structures are pure pneumatic structures and can accomplish visibly differentiated tension-compression interfunctioning in the same manner that it is accomplished by pneumatic structures, at the subvisible level of energy events.
701.02 When we use the six-strut tetrahedron tensegrity with tensegrity octahedra in triple bond, we get an omnidirectional symmetry tensegrity that is as symmetrically compressible, expandable, and local-load-distributing as are gas-filled auto tires.
702.00 Geodesics
702.01 We have a mathematical phenomenon known as a geodesic. A geodesic is the most economical relationship between any two events. It is a special case of geodesics which finds that a seemingly straight line is the shortest distance between two points in a plane. Geodesic lines are also the shortest surface distances between two points on the outside of a sphere. Spherical great circles are geodesics.
703.00 Geodesic-Tensegrity Molecular Kinetics of Pneumatic Systems
703.01 Geodesic domes can be either symmetrically spherical, like a billiard ball, or asymmetrically spherical, like pears, caterpillars, or elephants.
703.02 I prefer to stay with compound curvature because it is structurally stronger than either flat surfaces or simple cylindrical curvature or conical curvature. The new compound-curvature geodesic structures will employ the tensegrity principles. The comparative strength, performance, and weight tables show clearly that the geodesic- dome geometry is the most efficient of all compound-curvatured, omnitriangulated, domical structuring systems.
703.03 All geodesic domes are tensegrity structures whether or not the tension- compression differentiations are visible to the observer. Tensegrity geodesic spheres do what they do because they have the properties of hydraulically or pneumatically inflated structures. Pneumatic structures, such as footballs, provide a firm shape when inflated because the atmospheric molecules inside are impinging outward against the skin, stretching it into accommodating roundness. When more molecules are introduced into enclosures by the air pump, their overcrowding increases the pressure. All the molecules of gas have inherent geometrical domains of activity. The pressurized crowding is dynamic and not static.
703.04 A fleet of ships maneuvering under power needs more room than do the ships of the same fleet when docked side by side. The higher the speed of the individual ships, the greater the sea room required. This means that the enclosed and pressurized molecules in pneumatic structural systems are accelerated in outward-bound paths by the addition of more molecules by the pump and, without additional room, each must move faster to get out of the way of others.
703.05 The pressurized internal liquid or gaseous molecules try to escape from their confining enclosure. The outward-bound molecules impact evenly upon all the inside surface of the enclosure__for instance, upon all of the football's flexible inside skin when it is kicked in one spot from outside. Their many outward-bound impactings force the skin outwardly and firmly in all directions, and the faster they move, the more powerful the impact. This molecular acceleration is misidentified as pressures and firmness of the pneumatic complex. This molecular acceleration distributes the force loads evenly. The outward forces are met by the comprehensive embracement of all the tensile envelope's combined local strengths. All locally impacting external loads, such as the kick given to a point on the football's exterior, are distributed by all the enclosed atmospheric molecules to all of the skin in the innocuously low magnitudes.
703.06 The ability to determine quite accurately what the local loadings of any given pneumatic structure will be under varying conditions and forces is well known and is about as far as the pneumatic sciences have gone in explaining inflated structures. The comfortably equationed state of their art is adequate to their automobile-or-airplane-tire-, balloon-, or submarine-designing needs.
703.07 It is, however, possible to find out experimentally a great deal more about the behavior of those invisible, captive, atmospheric molecules and to arrive at a greater geo-mathematical understanding of the structural relationships between pneumatically inflated bags or vessels and geodesic tensegrity spheres and domes. It is thus possible also to design tensile structures that meet discretely, ergo nonredundantly, the patterns of outwardly impinging forces. It also becomes possible, for the first time, for structural engineers to analyze geodesic domes in a realistic and safe manner. Up to this time, the whole engineering profession has been analyzing geodesics on a strictly continuous- compression, crystalline, non-load-distributing, "post-and-lintel" basis. For this reason, the big geodesic domes thus far erected have been way overbuilt by many times their logically desirable two-to-one safety factor.
703.08 While the building business uses safety factors of four, five, or six-to-one, aircraft-building employs only two-to-one or even less because it knows what it is doing. The greater the ignorance in the art, the greater the safety factor that must be applied. And the greater the safety factor, the greater the redundancy and the less the freedom of load distribution.
703.09 First we recall, as has long been known experimentally, that every action has a reaction. For a molecule of gas to be impelled in one direction, it must "shove off from," or be impelled by, another molecule accelerated in an opposite direction. Both of the oppositely paired and impelled action and reaction molecules inside the pneumatically expanded domes will impinge respectively upon two chordally opposed points on the inside of the skin. The middle point of a circular chord is always nearer the center of the circle than are its two ends. For this reason, chords (of arcs of spheres) impinge outwardly against the skin in an acutely glancing angular pattern.
703.10 When two molecules accelerate opposingly from one another at the center of the sphere, their outward trajectories describe a straight line that coincides with the diameter of a sphere. They therefore impinge on the skin perpendicularly, i.e., at 180 degrees, and bounce right back to the sphere center. It is experimentally evidenced that all but two of the myriad molecules of the captive gas do not emanate opposingly from one another at the center of the sphere, for only one pair can occupy one point of tangent bounce-off between any two molecules. If other molecules could occupy the nucleus position simultaneously, they would have to do so implosively by symmetrical self- compression, allowing the sphere to collapse, immediately after which they would all explode simultaneously. No such pulsating implosion-explosion, collapse-and-expand behavior by any pneumatic balls has been witnessed experimentally.
703.11 Molecules of gas accelerating away from one another and trying to proceed in straight trajectories must follow both the shortest-distance geodesic law as well as the angular-reflectance law; they will carom around inside a sphere only in circular paths describing the greatest diameter possible, therefore always in great-circle or geodesic paths.
703.12 For the same reasons, molecules cannot be "stacked up" inside the sphere in parallel or lesser-circle latitude planes. We also found earlier that the molecules could not be exploding simultaneously in all directions from the center of the sphere. If thin, colored vapor streaks are introduced into a transparently skinned, pneumatically pressurized sphere, then only at first superficial observation do the smoke-disclosed molecular motions seem to be demonstrating chaotically random patterns. This is not the case, however, for everything in Universe is in motion and everything in motion is always traveling in the direction of least resistance, wherefore the great circle's inherent polar symmetries of interaction must impose polar order__an order that is hidden from the observer only by its articulative velocities, which transcend the human's optically tunable, "velocity-of- motions" spectrum range of apprehending and therefore appear only as clouds of random disorder. Brouwer's theorem shows that when x number of points are stirred randomly on a plane, it can be proved mathematically__when the stirring is stopped__that one of the points was always at the center of the total stirring, and was therefore never disturbed in respect to all the others. It is also demonstrable that any plane surface suitable for stirring things upon, must be part of a system that has an obverse surface polarly opposite to that used for the stirring, and that it too must have its center of stirring; and the two produce poles in any bestirred complex system.
703.13 Every great circle always intercepts any other great circle twice, the interception points always being 180-degree polar opposites. When two force vectors operating in great-circle paths inside a sphere impinge on each other at any happenstance angle, that angle has no amplitude stability. But when a third force vector operating in a great-circle path crosses the other two spherical great circles, a great-circle-edged triangle is formed with its inherently regenerated 180-degree mirror-image polar opposite triangle. With a myriad of successive inside surface caromings and angular intervector impingements, the dynamic symmetry imposed by a sphere tends to equalize the angular interrelationship of all those triangle-forming sets of three great circles which shuntings automatically tend averagingly to reproduce symmetrical systems of omnisimilar spherical triangles always exactly reproduced in their opposite hemispheres, quarterspheres, and octaspheres. This means that if there were only three great circles, they would tend swiftly to interstabilize comprehensively as the spherical octahedron all of whose surface angles and arcs (central angles) average as 90 degrees.
703.14 A vast number of molecules of gas interacting in great circles inside of a sphere will produce a number of great-circle triangles. The velocity of their accomplishment of this structural system of total intertriangulation averaging will seem to be "instantaneous" to the human observer. The triangles, being dynamically resilient, mutably intertransform one another, imposing an averaging of the random-force vectors of the entire system, resulting in angular self-interstabilizing as a pattern of omnispherical symmetry. The aggregate of all the inter-great-circlings resolve themselves typically into a regular pattern of 12 pentagons and 20 triangles; or sometimes more complexedly, into 12 pentagons, 30 hexagons, and 80 triangles described by 240 great-circle chords.
703.15 This is the pattern of the geodesic tensegrity sphere. The numbers of hexagons and triangles and chords can be multiplied in regular arithmetical-geometrical series, but the 12 pentagons, and only 12, will persist as constants; also, the number of triangles will occur in multiples of 20; also, the number of edges will always be multiples of six.
703.16 In the geodesic tensegrity sphere, each of the entirely independent, compressional chord struts represents two oppositely directioned and force-paired molecules. The tensegrity compressional chords do not touch one another. They operate independently, trying to escape outwardly from the sphere, but are held in by the spherical-tensional integrity's closed network system of great-circle connectors, which alone complete the great-circle paths between the ends of the entirely separate, nonintercontacting compressional chords.
704.00 Universal Joints
704.01 The 12-spoke wire wheel exactly opposes all tension, compression, torque, or turbining tendencies amongst its members. Universal joints of two axes or three axes of freedom are analogous to the wire wheel as a basic 12-degrees-of-freedom accommodating, controlling, and employing system whose effectiveness relies upon their discrete mechanical and structural differentiation and disposition of all tension and compression forces. All of these may be considered to be basic tensegrity systems. (See illustration 640.41B.)
704.02 The shafted axis of the two-axis universal joint tends to make it appear as a single-axis system. But it constitutes in actuality an octahedral tensegrity, with its yoke planes symmetrically oriented at 90 degrees to one another. The two-axis tensegrity has been long known and is often successfully employed by mechanics as a flexible-membrane coupling sandwiched between two diametrically opposed yoke-ended shafts, precessionally oriented to one another in a 90-degree star pattern. This only tensionally interlinked, i.e., universally jointed, drive shafting has for centuries been demonstrating the discontinuous compression and only tensionally continuous multiaxial, multidimensional symmetry of tensegrity structuring and energetic work transmission from here to there.
705.00 Simple Curvature: The Barrel

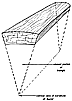Fig. 705.01 		705.01 The barrel represents an advanced phase of the Roman arch principle of stability accomplished by simple (approximately) single-axis curvature. A barrel is comprised of a complete ring around one axis of a number of parallel staves. A cross section cut through the barrel perpendicular to its single axis of curvature shows each of the stave's sections looking like keystones in an arch. Each stave is a truncated section of a triangle whose interior cutaway apex would be at the center of the barrel. The staves employ only the outer trapezoidal wedge-shaped cross section, dispensing with the unnecessary inner part of the triangle. The stave's cross section is wedge-shaped because the outer edge of the stave is longer than the inner edge of the stave. Because the stave's outer-circle chord is longer than its inner-circle chord, it cannot fall inwardly between the other staves and it cannot fall outwardly from close-packed association with the other staves because they are all bound inwardly together by the finitely closed barrel "hoops" of steel.

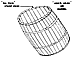Fig. 705.02 		705.02 All these barrel staves are lined in parallel to one another and are bound cylindrically. They constitute a finite, closed cylinder held together in compression by finitely encompassing tension bands, or hoops, which are parallel to one another and at 90 degrees to the axis of the staves. The staves cannot move outwardly due to the finiteness of the straps closing back upon themselves; they cannot fall inwardly on each other because their external chords are bigger than their internal chords. The tendency of internally loaded cylinders and vertically compressed columns to curve outwardly at their midgirth in their vertical profile is favored by designing and making the barrel staves of greater cross section at their midbarrel portions and the finite, closed-circle bands of lesser diameter near the ends than at the middle. The curving lines of compression thrust back against themselves, while the tension lines tend to pull true and form a finite closure, pressing the short, true chord sections of the staves tightly against one another in a complete circular arch; thus the staves may be flexed, when the barrel is internally filled, without tendency to failure.
705.03 Thus the barrel, when in good material condition, usually proves to be structurally stable and able to withstand the impact of dropping, especially when internally loaded, because the internal load tends to distribute any local shock load to all the enclosing barrel's internal surface and thence to the finitely closed, steel circle bands. Barrels constitute closed circuits of continuous tension finitely restraining discontinuous, though contiguously islanded, staves of compression in dynamic stability. Whether pressure is exerted upon its structure from outside or inside the barrel, the result is always an outward thrust of the staves against the tension members, whose finite closure and cross-sectional strength ultimately absorb all the working or random loads. The vertical forces of gravity in the primary working stresses of internally loaded, simple-curvature structures__such as those of the cylinder, barrel, tree trunk, or Greek column__are translated precessionally into horizontally outward buckling and torque stresses. When, however, such cylinders are not internally loaded and are turned over on their side with their axes horizontal, the stresses are precessed horizontally, outward from the cylinder ends toward the infinite poles of cylindrically paralleled stave lines. Under these conditions, the outer hoops' girth does not aid the structural interstabilization, and the forces of gravity acting vertically against the horizontally paralleled staves develop a lever arm of the topmost staves against the opposite outer staves of the barrel, tending to thrust open the sidemost staves from one another and thus allowing the integrity of the arch to be disintegrated, allowing infinity to enter and disintegrate the system.
705.04 Each of the barrel's tension hoops represents a separately operating, exclusively tensional circle with its plane parallel to, and remote from, the planes of the other, only separately acting, barrel hoops. The tension bands do not touch one another. The tension bands are only parallel to one another and act only at 90 degrees against the staves, which are also only parallel to one another. Neither the staves nor the tension hoops cross one another in such a manner as to provide intertriangulation and its concomitant structural self-stabilization. In fact, they both let infinity into the system to disintegrate it between the only parallel staves and hoops whose separate parts reach forever separately only toward infinity.
705.05 If we take a blowtorch and bum out one of the wooden staves, the whole barrel collapses because infinity floods in to provide enough space between the staves for their arch to be breached and thus collapse disintegratively. What the blowtorch does is to let infinity__or the nothingness of Universe__into the system to intrude between the discontinuous and previously only contiguously crowded together, exclusively compressional members of the system.
705.06 Barrels and casks, which provided great shipping and storage "container advantage" in the past, secured only by finite closure continuities of the only separately acting tension circles, were inherently very limited in structural efficiency due to the infinitely extendable__ergo, infinitely disassociative__staves as well as by the infinity that intruded disintegratively between the barrel's parallel sets of circular bands or hoops.
Next Section: 706.00
Copyright © 1997 Estate of R. Buckminster Fuller