706.00 Compound Curvature: Spherical Cask
706.01 Engineers and mathematicians both appear presently to be unfamiliar with practical means for discretely analyzing and employing the three-way grids of finitely closed, great-circle triangulations despite the fact that their triangular integrities constitute nature's most powerful and frequently employed structural systems. You can inform yourself experimentally regarding the relative structural effectiveness of flat, simple- cylinder, and compoundly curved sheet material by taking a flat piece of paper, standing it on its edges, and loading that top edge; you will note that it has no structural strength whatsoever__it just crumples. But if we roll-form the same piece of paper into a cylinder, which is what is called simple curvature, we can use the cylinder as a column in which all the compressionally functioning lines are parallel to each other and interact with the closed-circle tensional strength of the paper cylinder's outside surface like the staves and hoops of a barrel.
706.02 But only if we achieve a three-way interaction of great circles can we arrive at the extraordinary stability afforded by the omnitensionally integrated, triangular interstabilization of compound curvature. This we do experimentally with the same sheet of paper, which we now form into a conical shape. Standing the cone on its finitely closed circular base and loading its apex, we find it to be more stable and structurally effective for supporting a concentrated top loading than was either the first sheet or the simply curved cylinder. The top load now thrusts downwardly and outwardly toward the finitely closed, tensionally strong base perimeter, which becomes even stronger if the cone is foldingly converted into a tetrahedron whose insideness concavity and outsideness convexity and omnifinite tensional embracement constitute the prime manifestation of so-called "compound curvature."
706.03 In contrast to our simply curved, cylindrical barrel construction, let us now make a wooden geodesic sphere in which all of the triangular facets are external faces of internally truncated tetrahedra whose interior apexes, had they not been snubly truncated, would each have reached the center of the sphere. Each of the outwardly triangular, internally truncated, tetrahedral cork's edges is covered by finitely closed great-circle tension straps. The steel tension straps are not parallel to each other but are omnitriangularly interconnected to form a spherical barrel. Every great circle of a spherical cask crosses all other great circles of that sphere twice. Any two such__only polarly interconnected__great circles can hinge upon each other like a pair of shears. They are angularly unstable until a third great circle that does not run through the same crossings of the other two inherently crosses both of the first two great circles and, in effect, taking hold of the lever ends of the other two great circles, with the least effort accomplishes stabilization of the oppositely converging angle.
706.04 So we now have an omnitriangulated geodesic sphere of triangulated wooden plugs, or hard wooden corks fashioned of the same barrel stave oak, each one surrounded by and pressed tightly against three other such triangular hardwood corks; each has its exterior triangular facets edged by three great circles whose lengths are greater than the respectively corresponding wooden cork triangle's interior chords so that none of the wooden corks can fall inwardly. The finitely closed great-circle straps are fastened to each other as they cross one another; thus stably interpositioned by triangulation, they cannot slip off the sphere; and none of the wooden triangular corks can fall in on one another, having greater outer edge lengths than those of their inner edges. The whole sphere and its spherical aggregates of omnitriangularly corked surface components are held tightly together in an omnitriangulated comprehensive harness. All of the great circles are intertriangulated in the most comfortable, ergo most economical, interpositions possible.
706.05 If we now take a blowtorch and bum out entirely one of the triangular, truncated wooden corks__just as we burned out one of the barrel's wooden staves__unlike the barrel, our sphere will not collapse. It will not collapse as did the regular barrel when one stave was burnt out. Why does it not collapse? Because the three- way triangular gridding is finitely closed back on itself. Infinity is not let into the system except through the finitely-perimetered triangular hole. The burning out of the triangular, truncated tetrahedron, hardwood cork leaves only a finite triangular opening; and a triangular opening is inherently a stable opening. We can go on to bum out three more of the triangular, truncated wooden corks whose points are adjacent to each other, and while it makes a larger opening, it remains a triangular opening and will still be entirely framed with closed and intertriangulated great circles; hence it will not collapse. In fact, we find that we can bum out very large areas of the geodesic sphere without its collapsing. This three-way finite crossing of most economical great circles provides a powerful realization of the fundamentals of compound curvature. Compound curvature is inherently self- triangulating and concave-convexing the interaction of those triangles around the exterior vertexes.
706.10 Sphericity: Compound curvature, or sphericity, gives the greatest strength with the least material. It is no aesthetic accident that nature encased our brains and regenerative organs in compoundly curvilinear structures. There are no cubical heads, eggs, nuts, or planets.
706.20 Three-Way Great Circling: While great circles are the shortest distances around spheres, a single great-circle band around a sphere will readily slide off. Every great circle of a sphere must cross other great circles of that sphere twice, with the crossings of any two always 180 degrees apart. Since an infinite number of great circles may run through any two same points on a sphere 180 degrees apart, and since any two great-circle bands are automatically self-interpolarizing, two great-circle bands on a sphere can rotate equatorially around their mutual axis and attain congruency, thereafter to act only as one solitary meridian, and therefore also free to slide off the sphere. Not until we have three noncommonly polarized, great-circle bands providing omnitriangulation as in a spherical octahedron, do we have the great circles acting structurally to self-interstabilize their respective spherical positionings by finitely intertriangulating fixed points less than 180 degrees apart.
706.21 Since great circles describe the shortest distances between any two spherical points less than 180 degrees apart, they inherently provide the most economical spherical barrel bandings.
706.22 The more minutely the sphere is subtriangulated by great circles, the lesser the local structural-energy requirements and the greater the effectiveness of the mutual- interpositioning integrity. This spontaneous structural self-stabilizing always and only employs the chords of the shortest great-circle arc distances and their respective spherical finiteness tensional integrity.
706.23 When disturbed by energy additions to the system, the triangular plug "corks" can only__and precessionally "prefer"__to be extruded only outwardly from the system, like the resultant of all forces of all the kinetic momentums of gas molecules in a balloon. The omni-outwardly straining forces of all the compressional forces are more than offset by the finitely closed, omni-intertriangulated, great-circle tensions, each of whose interstitial lines, being part of a triangle__or minimum structure__are inherently nonredundant. The resultant of forces of all the omni-intertriangulated great-circle network is always radially, i.e. perpendicularly, inward. The tightening of any one great circle results in an even interdistribution of the greater force of the inward-outward balance of forces.
706.30 Fail-Safe Advantages: With each increase of frequency of triangular module subdivisions of the sphere's unitary surface, there is a corresponding increase in the fail-safe advantage of the system's integrity. The failure of a single triangular cork in an omnitriangulated spherical grid leaves a triangular hole, which, as such, is structurally innocuous, whereas the failure of one stave in a simple-curvature barrel admits infinity and causes the whole barrel to collapse. The failure of two adjacent triangular corks in a spherical system leaves a diamond-shaped opening that is structurally stable and innocuous; similarly, the failure of five or six triangles leaves a completely arched, finitely bound, and tensionally closed pent or hex opening that, being circumferentially surrounded by great circles, is structurally innocuous. Failure of a single spherical-tension member likewise leaves an only slightly relaxed, two-way detoured, diamonded relaying of the throughway tensional continuity. Considerable relaxing of the spherical, triangulated-cork barrel system by many local tension failures can occur without freeing the corks to dangerously loosened local rotatability, because the great-circle crossings were interfastened, preventing the tensionally relaxed enlargement of the triangular bonds. The higher the frequency and the deeper the intertrussing, the more fail-safe is this type of spherical structure.
706.31 Structural systems encompassing radial compression and circumferential tension are accomplished uniquely and exclusively through three-way spherical gridding. These radial and circumferential behaviors open a whole new field of structural engineering formulations and an elegance of refinement as the basis for a new tensegrity- enlightened theory of engineering and construction congruent with that of Universe.
707.00 Spherical and Triangular Unity
707.01 Complex Unity and Simplex Unity: The sphere is maximal complex unity and the triangle is minimal simplex unity. This concept defines both the principles and the limits governing finite solution of all structural and general-systems-theory problems.
707.02 Local isolations of "point" fixes, "planes," and "lines" are in reality only dependent aspects of larger, often cosmically vast or micro-, spheric topological systems. When local isolation of infinitely open-ended planes and linear-edged, seemingly flat, and infinite segments are considered apart from their comprehensive spherical contexts, we are confronted with hopelessly special-cased and indeterminate situations.
707.03 Unfortunately, engineering has committed itself in the past exclusively to these locally infinite and inherently indeterminate systems. As a consequence, engineering frequently has had to rely only on such trial-and-error-evolved data regarding local behaviors as the "rate" of instrumentally measurable deflection changes progressively produced in static-load increases, from which data to evolve curves that theoretically predict "failure" points and other critical information regarding small local systems such as columns, beams, levers, and so forth, taken either individually or collectively and opinionatedly fortified with safely "guesstimated" complex predictions. Not until we evolve and spontaneously cultivate a cosmic comprehension deriving from universal, finite, omnitriangulated, nonredundant structural systems can we enjoy the advantage of powerful physical generalizations concisely describing all structural behaviors.

710.00 Vertexial Connections

710.01 When a photograph is made of a plurality of lines crossing through approximately one point, it is seen that there is a blurring or a running together of the lines near the point, creating a weblike shadow between the converging lines__even though the individual lines may have been clearly drawn. This is caused by a refractive bending of the light waves. When the masses of the physically constituted lines converge to critical proximity, the relative impedance of light-wave passage in the neighborhood of the point increases as the second power of the relative proximities as multiplied by a factor of the relative mass density.
710.02 Tensegrity geodesic spherical structures eliminate the heavy sections of compression members in direct contact at their terminals and thus keep the heavy mass of respective compressions beyond critical proximities. As the vertexial connections are entirely tensional, the section mass is reduced to a minimum, and system "frequency" increase provides a cube-root rate of reduction of section in respect to each doubling frequency. In this manner, very large or very small tensegrity geodesic spheroids may be designed with approximate elimination of all microwave interferences without in any way impairing the structural dimensional stability.
710.03 The turbining, tensionally interlaced joints of the tensegrity-geodesic spheroids decrease the starlike vertexial interference patterns.
711.00 Gravity as a Circumferential Force
711.01 Circumference: Circumference = 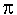D = C. Wherefore, we can take a rope of a given D length and lay it out circumferentially to make it a circle with its ends almost together, but with a tiny gap between them.
711.02 Then we can open out the same rope to form only a half-circle in which the diameter doubles that of the first circle and the gap is wide open.
711.03 Halfway between the two, the gap is partially open.
711.04 As we open gaps, we make the sphere bigger. The comprehensive tension wants to make it smaller. Struts in the gap prevent it from becoming smaller. Struts make big. Tension makes small. The force of the struts is only outward. The force of the tension network is only inward.
711.10 Circumferential Advantage over Radial: Gravity is a spherically circumferential, omniembracingly contractive force. The resultant is radially inward, attempting to make the system get smaller. The circumferential mass-interattraction effectiveness has a constant coherent advantage ratio of 12 to 1 over the only radially effective mass attraction; ergo, the further inward within the embraced sphere, the greater the leverage advantage of the circumferential network over the internal compaction; ergo, the greater the radial depth within, the greater the pressure.
711.20 Ratio of Tensors: Locally on a circle, each particle has two sideways tensors for each inward tensor. One great-circle plane section through a circle shows two sideways tensors for one inward vector. But, on the surface of a sphere, each particle has six circumferential tensors for each single inward radial vector. When you double the radius, you double the chord.
711.30 Struts as Chords in a Spherical Network: When inserting a strut into a tensegrity sphere, we have to pull the tension lines outward from the system's center, in order to insert the strut between the vertexes of those lines. As we pull outward, the chordal distance of the gap between the spheric tension lines increases.
711.31 If we wish to open the slot in the basketball or football's skin through which its pneumatic bladder is to be inserted, we pull it outwardly and apart to make room inside.
711.32 The most outward chord of any given central angle of a circle is the longest. The omnicircumferential, triangularly stabilized, interconnecting tension lines of the spherical-network system cannot get bigger than its discretely designed dimensions and the ultimate tensile strength of the network's tensors, without bursting its integrity. The comprehensive spherical-tensor network can only relax inwardly. When all in place, the tensegrity-compression struts can only prevent the tension network from closing inward toward the sphere's center, which is its comprehensive proclivity.
711.33 The synergetic force of the struts (that is, their total interrelationship tendency) is not predicted by any one strut taken singly. It is entirely omniradially outward. The force of the strut is not a chordal two-way thrust.
711.34 A fully relaxed spherical tensegrity structure may be crumpled together in a tight bundle without hurting it, just as a net shopping bag can be stuffed into a small space. Thereafter, its drooped, untaut tension members can only yield outward radially to the dimensionally predesigned and prefabricated limits of the omniclosed spheric system, which must be progressively opened to accommodate the progressive interconstruction of the predesigned, prefabricated chordal lengths of the only circumferentially arrayed compression struts.
711.35 The compression struts are islanded from one another, that is, in each case, neither of the separate compression strut's ends touches any part of any other compression strut in the spheric system. As struts are inserted into the spheric-tension network, the whole spheric system is seen to be expanding omnioutwardly, as do pneumatic balloons when air is progressively introduced into their previously crumpled skins.
711.36 The comprehensive, finitely closed tension network's integrity is always pulling the islanded compression struts inward; it is never pushing them, nor are they pushing it, any more than a rock lying on Earth's crust thrusts horizontally sidewise. The rock is held where it is by the comprehensively contractive Earth's inter-mass-attraction (gravitational) field, or network. But the more rocks we add, the bigger the sphere held comprehensively together by the omnitensively cohering, gravitational consequences of the omni-interattractive mass aggregate.
712.00 Clothesline

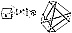Fig. 712.01 		712.01 Surprising behaviors are found in tensegrity structures. The illustration shows a house and a tree and a clothesline. The line hangs low between the house and the tree. To raise the line so that the clothes to be dried will not sweep the ground, the line is elevated by a pole that has one end thrust against the ground and the other end pushed outwardly against the line. The line tightens with the pole's outer end at the vertex of an angle stretched into the line. The line's angle shows that the line is yielding in the direction away from the thrusting pole.
712.02 As the clothesline tightens and bends, it always yields away from the pushing strut. In spherical tensegrity structures the islanded compression struts pull the tension lines to angle toward the strut ends.
712.03 When we release a compression member from a tensegrity sphere, one end does not thrust by the tension member to which it was fastened in a circumferential direction. It was not fastened in thrust or sheer. It was not pushing circumferentially. It was resisting being compressed, and like a cork in a bottle, it was employing its frictional contact with the tension net at both its ends to resist its only tendency, which was to exit radially outward from the system's center.
713.00 Discontinuous Compression
713.01 Subvisible Discontinuity: In the Babylonian, Egyptian, and Ionian eras of ways of looking at, thinking about, and formulating, there evolved a concept of a "first family" of geometrical "solids," in which each member was characterized by all of its faces being identical and all of its edges being one length only. Humans were then unaware of what physics was only much later to discover experimentally: that nature discloses no evidence of a continuum. Experiment discloses only aggregates of separate, finitely closed events. Ergo, there are no solids.
713.02 Their optical illusion and stubbornly conditioned reflexes have since motivated one generation after another to go on teaching and accepting the misconception of geometric "solids," "planes," and "straight lines," where physics has discovered only wavilinear trajectories of high-frequency, yes-no event pulsations. With the misconception of straight lines came the misconception of the many lines going through the same point at the same time. Wherefore the 12 edges that define the cube were assumed to be absolute straight lines, and therefore sets of them ran simultaneously into the thus absolutely determined eight corner "points" of the cube.
713.03 Humans were accustomed to the idea that edges come together at one certain point. But we now know operationally that if we look at any of the edges of any item microscopically, there is no such absolute line, and instead there is seen to be an aggregate of atomic events whose appearance as an aggregate is analogous to the roughly rounding, wavilinear profiled, shoulder "edge" of a rock cliff, sand, or earth bluff standing high above the beach of the shore lying below, whose bluff and beach disclose the gradual erosion of the higher land by the sea.
713.04 The corners of the solids are also just like the corners of an ocean-side bluff that happens to have its coastwise direction changed at 90 degrees by large geological events of nature such as an earthquake fault. Such an easterly coastline's bluff casts dark shadows as the Earth rotates; seen from airplanes at great altitudes, long sections of that black coastal shadow may appear illusionarily as "straight."
713.05 We can make Platonic figures in nonsolid tensegrity where none of the lines go through any of the same points at the same time, and we realize that the only seemingly continuous, only mass-interattractively cohered, atomic "Milky Way" tensor strands spanning the gaps between the only seemingly "solid," omni-islanded, vectorially compressioned struts, do altogether permit a systematic, visually informed, and realistically comprehended differentiation between the flexible tensor and inflexible vector energy-event behaviors, all of which are consistent with all the experimental information accruing to the most rigorous scientific discipline.
713.06 The eye can resolve intervals of about 1/100th of an inch or larger. Below that, we do not see the aggregates as points. Thereafter, we see only "solid"-color surfaces. But our color receptivity, which means our only-human-optics-tunable range of electromagnetic radiation frequencies, cannot "bring in," i.e., resonatingly respond to, more than about one-millionth of the now known and only instrumentally tune-in-able overall electromagnetic-wave-frequency range of physical Universe. This is to say that humans can tune in directly to less than one-millionth of physical reality__ergo, cannot "see" basic atomic and molecular-structuring events and behaviors, but our synergetic tensegrity principles of structuring are found instrumentally to be operative to the known limits of both micro- and macro-Universe system relationships as the discontinuous, entropic, radiational, and omnicohering, collecting gravitational syntropics. (See Sec. 302..)
713.07 Convergence: While we cannot see the intervals between atomic-event waves, the tensegrity structuring principles inform our consideration of the invisible events. Every time we instrumentally magnify the illusionarily converging geometrical "lines" defining the edges of "solids," we see them only wavilinearly converging toward critical proximity but never coming completely together; instead, twisting around each other, then slivering again, never having gone through the same "points."
713.08 When we first try to differentiate tension and compression in consciously attempting to think about the behavior of structures in various locals of Universe, it becomes apparent that both macro-Universe and micro Universe are only tensionally cohered phenomena. They both obviously manifest discontinuous compression islands. It is evidenced, in cosmically structured systems, both macro and micro, that compression members never touch one another. Earth does not roll "ball bearing" around on the surface of Mars; nor does the Moon roll on Earth, and so forth. This structural scheme of islanded spheres of compression, which are only mass-attractively cohered, also characterizes the atomic nucleus's structural integrities. Tensegrity discoveries introduce new and very different kinds of structural principles which seem to be those governing all structuring of Universe, both macrocosmic and microcosmic.
713.20 Compression Members
713.21 Behavior of Compression Members in Spherical Tensegrity Structures: In spherical tensegrity constructions, whenever a tension line interacts with a compression strut, the line does not yield in a circumferential direction away from the strut. The islanded compression member, combining its two ends' oppositely outward thrust, pulls on the omni-integrated tension network only acting as a radially outward force in respect to the sphere's center.
713.22 When we remove a compression member from a tensegrity sphere of more than three struts, the compression member of the original triangular group, when released on one end, does not shove by the tension member to which it was fastened. It is not fastened in shove or sheer. It pulls outwardly of the spherical system, away from the tension members at both of its ends simultaneously; when released, it pops only outwardly from the sphere's center.
713.23 When inserting a strut into a tensegrity sphere, you are pulling the tensional network only outwardly of the system in order to allow the strut to get into the system, that is, toward the structure's center. The strut pulls only outward on the two adjacent tension members to which it is fixed, trying to escape only radially outwardly from the system's center.
Next Section: 714.00
Copyright © 1997 Estate of R. Buckminster Fuller