725.00 Transformation of Tensegrity Structures

725.01 Six-strut tensegrity tetrahedra can be transformed in a plurality of ways by changing the distribution and relative lengths of its tension members to the six-strut icosahedron.

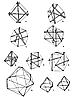Fig. 725.02

725.02 A theoretical three-way coordinate expansion can be envisioned, with three parallel pairs of constant-length struts, in which a stretching of tension members is permitted as the struts move outwardly from a common center. Starting with a six-strut octahedron, the structure expands outwardly, going through the icosahedron phase to the vector-equilibrium phase.

725.03 When the structure expands beyond the vector equilibrium, the six struts become the edges of the figure; they consequently lose their structural function (assuming that the original distribution of tension and compression members remains unchanged). As the tension members become substantially longer than the struts, the struts tend to approach relative zero, and the overall shape of the structure approaches a super octahedron.

726.00 Six-Pentagonal Tensegrity Sphere

726.01 The Symmetrical, Six-Great-Circle-Planed, Pentagonally Equatored Tensegrity Sphere: A basic tensegrity sphere can be constituted of six equatorial-plane pentagons, each of which consists of five independent and nonintertouching compression struts, totaling 30 separate nonintertouching compression struts in all. This six-pentagon- equatored tensegrity sphere interacts in a self-balanced system, resulting in six polar axes that are each perpendicular to one of its six equatorial pentagonal planes. Twelve lesser- circle-planed polar pentagons are found to be arrayed perpendicular to the six polar axes and parallel to the equatorial pentagon planes. It also results in 20 triangular interweavings, which structuring stabilizes the system.

726.02 Instead of having cables connecting the ends of the struts to the ends of the next adjacent struts in the six-axes-of-symmetry tensegrity structure, 60 short cables may be led from the ends of each prestressed strut either to the midpoint of the next adjacent strut or to the midpoint of tension lines running from one end to the other of each compression strut. Each of the two ends of the 30 spherical-chord compression struts emerges as an energy action? out over the center of action-and-reaction-effort vectors of the next adjacent strut, at which midpoint the impinging strut's effort is angularly precessed to its adjacent struts. Thus each strut precessionally transfers its effort and relayed interloadings to the next two adjacent struts. This produces a dynamically regenerative, self-interweaving basketry in which each compression strut is precessed symmetrically outwardly from the others while simultaneously precessing inwardly the force efforts of all the tensional network.

726.03 In this pattern of six separate, five-strut-membered pentagons, the six pentagonal, unsubstanced, but imaginable planes cut across each other equiangularly at the spheric center. In such a structure, we witness the cosmic principles that make possible the recurrence of locally regenerative structural patterns. We are witnessing here the principles cohering and regenerating the atoms. The struts are simple, dynamic, energy- event vectors that derive their regenerative energies from an eternally symmetrical interplay of inbound-outbound forces of systems that interfere with one another to maintain critical fall-in, shunt-out proximities to one another.

730.00 Stabilization of Tension in Tensegrity Columns

730.10 Symmetric Juxtaposition of Tetrahedra

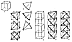Fig. 730.11

730.11 All polyhedra may be subdivided into component tetrahedra. Every tetrahedron has four vertexes, and every cube has eight vertexes. Every cube contains two tetrahedra (ABCD and WXYZ). Each of its faces has two diagonals, the positive set and the negative set. These may be called the symmetrically juxtaposed positive and negative tetrahedra, whose centers of volume are congruent with one another as well as congruent with the center of volume of the cube. It is possible to stack cubes into two columns. One column can demonstrate the set of positive tetrahedra, and the other column can demonstrate the set of negative tetrahedra.

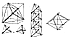Fig. 730.12

730.12 In every tetrahedron, there are four radials from the center of volume to the four vertexes. These radials provide a model for the behavior of compression members in a column of tensegrity-stacked cubes. Vertical tension stays connect the ends of the tetrahedral compression members, and they also connect the successive centers of volume of the stacked spheres__the centers of volume being also the junction of the tetrahedral radials. As the two centers of volume are pulled toward one another by the vertical tension stays, the universally jointed radials are thrust outwardly but are finitely restrained by the sliding closure XYZW interlinking the tetrahedral integrities of the successive cubes.

730.13 This system is inherently nonredundant, as are all discontinuous- compression, continuous-tension tensegrity structures. The approximately horizontal slings cannot come any closer to one another, and the approximately vertical stays cannot get any farther from one another; thus they comprise a discrete-pattern, interstabilizing relationship, which is the essential characteristic of a structure.

740.00 Tensegrity Masts: Miniaturization

740.10 Positive and Negative

740.11 Stacked columns of "solidly," i.e., compressionally continuous and only compressionally combined, cubes demonstrate the simultaneous employment of both positive and negative tensegrities. Because both the positive and the negative tensegrity mast are independently self-supporting, either one provides the same overall capability. It is a kind of capability heretofore associated only with "solid" compressional struts, masts, beams, and levers__that is, either the positive- or the negative-tensegrity "beam-boom- mast" longitudinal structural integrity has the same capability independently as the two of them have together. When the two are combined, either the positive- or the negative- tensegrity set, whichever is a fraction stronger than the other, it is found experimentally, must be doing all the strut work at any one time. The unemployed set is entirely superfluous, ergo redundant. All "solid" structuring is redundant.

740.12 If the alternate capabilities of the positive and negative sets are approximately equal, they tend to exchange alternately the loading task and thus generate an oscillating interaction of positive vs. negative load transferral. The energies of their respective structural integrities tend to self-interdeterioration of their combined, alternating, strut-functioning longevity of structural capability. The phenomenon eventually approaches crystallization. All the redundant structures inherently accelerate their own destruction in relation to the potential longevity of their nonredundant tensegrity counterparts.

740.20 Miniaturization

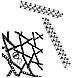Fig. 740.21

740.21 It is obvious that each of the seemingly "solid" compression struts in tensegrity island complexes could be replaced by miniature tensegrity masts. There is nothing to keep us from doing this but technological techniques for operating at microlevels. It is simply that each of the struts gets smaller: as we look at each strut in the tensegrity mast, we see that we could make another much smaller miniature tensegrity mast to replace it. Every time we can see a separate strut and can devise means for making a tensegrity strut of that overall size, we can substitute it for the previously "solid" strut. By such a process of progressive substitutions in diminishing order of sizes, leading eventually via sub-sub-sub-miniaturizing tensegrities to discovery of the last remaining stage of the seemingly "solid" struts, we find that there is a minimum "solid-state" strut's column diameter, which corresponds exactly with two diameters of the atoms of which it is constructed. And this is perfectly compatible, because discontinuity characterizes the structuring of the atoms. The atom is a tensegrity, and there are no "solids" left in the entire structural system. We thus discover that tensegrity structuring and its omnirationally constituted regularities are cosmically a priori, disclosing that Universe is not redundant. It is only humanity's being born ignorant that has delayed all of humanity's escape from the self-annihilating effect of the omniredundance now characterizing most of humanity's activities.

740.30 No Solids in Structures

740.31 There are no solids in structures. Ergo, there are no solids in Universe. There is nothing incompatible with what we may see as "structure" at the superficial level and what we are finding out to be the structural relationships in nuclear physics. It is just that we did not have the information when yesterday we built so solidly. This eliminates any further requirement of the now utterly obsolete conception of "solid" anything as intervening in the man-tuned sensorial ranges between the macro- and micro-world of ultra- and infrasensorial integrity. We have tensegrity constellations of stars and tensegrity constellations of atoms, and they are just Milky Way-like star patterns of relative spaces and critical proximities.

750.00 Unlimited Frequency of Geodesic Tensegrities

750.10 Progressive Subdividing

750.11 The progressive subdivision of a given metal fiber into a plurality of fibers provides tensile capabilities of the smaller fibers at increased magnitudes up to hundreds and thousandsfold that of the originally considered unit section. This is because of the increased surface-to-mass ratios and because all tensile capability of structure is inherently invested in the external beginnings of structural systems, which are polyhedra, with the strength enclosing the microcosm that the structural system inwardly isolates.

750.12 Geodesic tensegrity spheres are capable of mathematical treatment in such a manner as to multiply the frequency of triangular modular subdivision in an orderly second-power progression. As relative polyhedral size is diminished, the surface decreases at a velocity of the second power of the linear-dimension shrinkage, while the system volume decreases at a velocity of the third power. Weight-per-surface area relates directly to the surface-to-volume rate of linear-size decrease or increase.

750.20 Unlimited Subdivisibility of Tensional Components

750.21 The higher the frequency, the greater the proportion of the structure that is invested in tensional components. Tensional components are unlimited in length in proportion to their cross-section diameter-to-length ratios. As we increase the frequency, each tension member is parted into a plurality of fibers, each of whose strength is multiplied many times per unit of weight and section. If we increase the frequency many times, the relative overall weight of structures rapidly diminishes, as ratioed to any linear increase in overall dimension of structure.

750.22 The only limit to frequency increase is the logistic practicality of more functions to be serviced, but the bigger the structure, the easier the local treatability of high-frequency components.

750.23 In contrast to all previous structural experience, the law of diminishing returns is operative in the direction of decreasing size of geodesic tensegrity structures, and increasing return is realized in the direction of their increasing dimensions.