 |
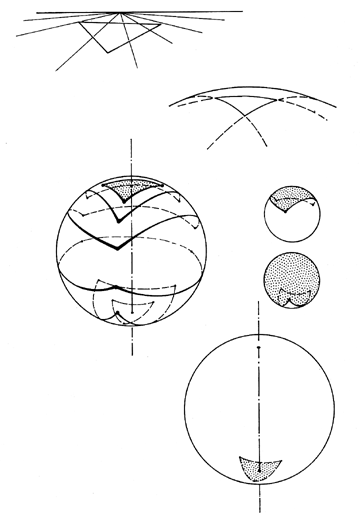
| Fig. 812.03: The Greeks defined a triangle as an area bound by a closed line of three edges and three angles. A triangle drawn on the Earth's surface is actually a spherical triangle described by three great- circle arcs. It is evident that the arcs divide the surface of the sphere into two areas, each of which is bound by a closed line consisting of three edges and three angles, ergo dividing the total area of the sphere into two complementary triangles. The area apparently "outside" one triangle is seen to be "inside" the other. Because every spherical surface has two aspects_convex if viewed from outside, concave if viewed from within_each of these triangles is, in itself, two triangles. Thus one triangle becomes four when the total complex is understood. "Drawing" or "scribing" is an operational term. It is impossible to draw without an object upon which to draw. The drawing may be by depositing on or by carving away, that is, by creating a trajectory or tracery of the operational event. All the objects upon which drawing may be operationally accomplished are structural systems having insideness and outsideness. The drawn-upon object may be symmetrical or asymmetrical, a piece of paper or a blackboard system having insideness and outsideness. |