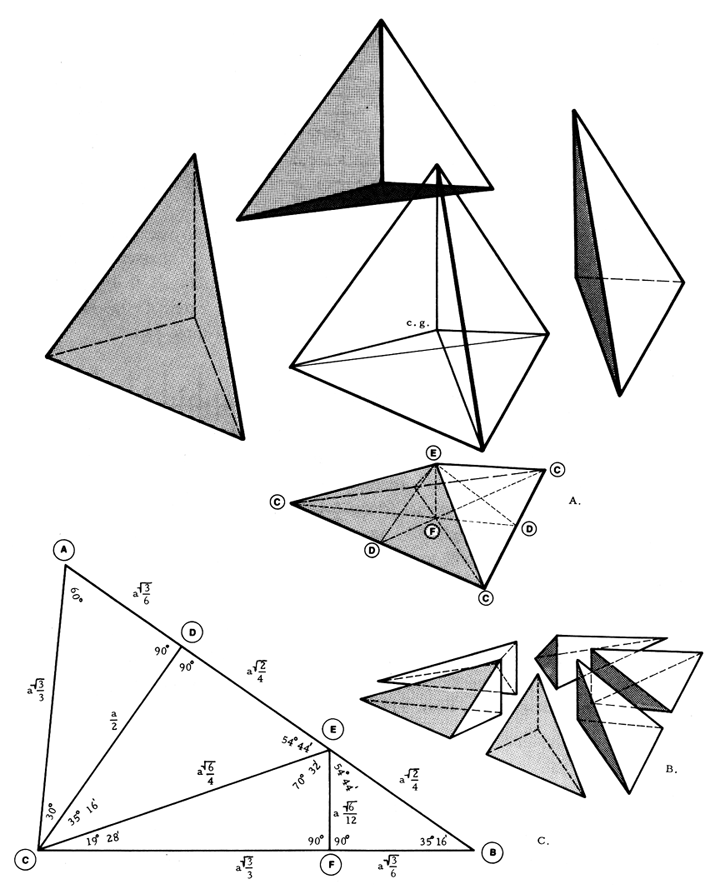
Fig. 913.01 Division of the Quarter-Tetrahedron into
Six Parts: A Quanta Module:
- The regular tetrahedron is divided volumetrically
into four identical quarters.
- The quarter-tetrahedron is divided into six identical
irregular tetrahedra, which appear as three
right-hand and three left-hand volumetric units each
equal in volume to 1/24th of the original
tetrahedron. This unit is called the A Module.
- The plane net which will fold into either left or
right A modules is shown. Vertex C is at the vertex
of the regular tetrahedron. Vertex E is at the center
of gravity of the tetrahedron. Vertex D is at the
mid-edge of the tetrahedron. Vertex F is at the center
of the tetrahedron face. Note that AD = FB, DE
= EB, and AC = CF.
|