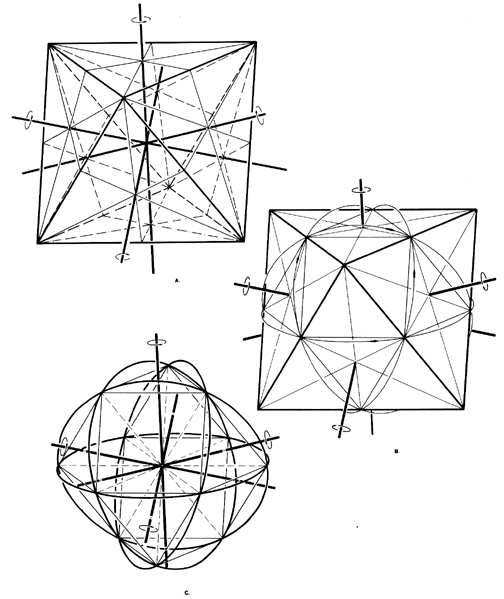
Fig. 987.221 Four-great-circle Systems of Octahedron
and Vector Equilibrium: Symmetry #2:
- Six-great-circle fractionation of octahedron (as
shown in Figs.
987.240 B and C) defines centers of
octa faces; interconnecting the pairs of opposite octa
faces provides the octahedron's four axes of
symmetry__here shown extended.
- Four mid-face-connected spin axes of octahedron generate
four great circle trajectories.
- Octahedron removed to reveal inadvertent definition
of vector equilibrium by octahedron's four great
circles. The four great circles of the octahedron and
the four great circles of the vector equilibrium
are in coincidental congruence. (The vector equilibrium
is a truncated octahedron; their triangular
faces are in parallel planes.)
|