|
Historically long perspective
Suggests it as possible
That many of the intriguing
Yet ineffable experiences
Which humanity thus far
Has been unable to explain,
And, therefore, treats with only superstitiously,
May embrace phenomena
Which in due course
Could turn out to be complexes
Of physically demonstrable realities
Which might even manifest
Generalized principles of Universe.
For this and similar reasons
I have paid a lot of attention
To ancient numerology,
Thinking that it might contain
Important bases for further understanding
Of the properties of mathematics
And of the intertransformative
Structurings and destructurings
Of the cosmic scenario yclept
"Eternally self-regenerative Universe."
My intuition does not find it illogical
That humanity has developed and retained
The demisciences of
Astrology and numerology__
Demi because they are
Only partially fortified by experimental proofs__
Which nonetheless challenge us tantalizingly
To further explorations
Within which it may be discovered
That generalized scientific laws
Are, indeed, eternally operative.
Our observational awareness
And Newton's proof
Of the mass-attraction law
Governing the Moon's powerful tidal pull
On the Earth's oceans,
In coincidence with our awareness
Of the Moon phase periodicities
Of female humans' menstrual tides,
Gave the Moon's (men's month's) name
To that human blood flow.
Conceivably there could be
Many other effects of celestial bodies
Upon terrestrially dwelling human lives.
In the late 1930s,
When I was science and technology consultant
On its editorial staff, with Russell Davenport
Then managing editor, of Fortune magazine,
I found him to be deeply involved with astrology.
Russell couldn't understand why I was not actively excited
By the demiscience__astrology,
Since the prime celestial data derived
From scientific observations.
I was not excited
Because I had no experience data
That taught me incisively
Of any unfailingly predictable influence
Upon myself or other Earthians
Which unerringly corresponded
With the varying positions of the solar planets
At the time of the respective human births.
While the planetary interpositionings
At any given time had been scientifically established,
I had no scientifically cogent means for exploring
Their effect upon terrestrial inhabitants.
On the other hand, I found many cogent clues
For exploring the ancient demiscience of numerology.
Ancient numerologists developed
Many tantalizingly logical theories,
Some of which were
Partially acceptable to formal mathematics,
Such as enumeration by "congruence in modulo eight,"
Or, "congruence in modulo ten,"
Or in increments of twelve.
"Congruence in modulo ten" seemed
Obviously induced by
The convenience of the human's ten fingers
As memory-augmenting,
Sequentially bendable,
Counting devices of serial experiences.
Their common appendages of ten fingers each
Provided humans with "natural" and familiar sets
Of experience aggregates
To match with other newly experienced aggregates
As congruent sets.
There was also the popular enumeration system
Based on modulo twelve.
Human counting systems of twelve were adopted
Because the decimal system
Does not rationally embrace
The prime number three.
Since humanity had so many threefold experiences,
Such as that of the triangle's stability,
Or that of the father-mother-child relationships,
Humanity needed an accounting system
That could be evenly and alternatively subdivided
In increments either
Of one, or two, or three.
Ergo, "congruence in modulo twelve"
Was spontaneously invented.
"Invention" means
To bring into novel special-case use
An eternal and universal principle
Which scientific experiment and comprehension
May attest to be generalized principles.
"Etymology" means
The scientific study of words and their origin.
Through etymology man gave names
To their abstract number set concepts.
English is a crossbred
Worldian language.
It is interwoven with Anglo-Saxon,
Old German, Sanskrit, Latin and Greek roots
Interspersed with Polynesian, Magyar, Tatar, et al.
The largest proportion of English words
Are derived from India's Sanskrit,
Which itself embraces hundreds
Of lesser known root languages.
There are a few words whose origins
Have thus far defied scientific identification.
There are not many unidentified root words.
Those of unknown origins
Are classified etymologically as "Old Words."
All but one of the world-around
Words or "names" for numbers
Are classified etymologically as "Old Words."
The one exception is the name for "five,"
Whose conceptual derivation comes directly or indirectly
From word roots identifying the human "hand."
None of the other names for numbers
In any of the human languages
Have pragmatic identifiability
With names for any other known
Physical-experience concepts.
To accommodate the cerebrations
Of those who are reflexively conditioned
To recount their experiences
In twelvefold aggregates__
That is, "congruence in modulo twelve"__
Unique names were etymologically evolved
For the numbers eleven and twelve
As well as for the numbers one through ten.
In the new world-around-accepted computational system
Of "congruence in modulo ten"__
That is, the decimal system__
The numbers zero through ten
Are called "cardinal" numbers.
But the English names "eleven" and "twelve,"
Or French names "onze" and "douze,"
Or the Germans' "elf" and "zwoelf,"
Likewise are cardinal numbers
In the duodecimal system,
And their cardinal names are used
Even when employed in the decimal system.
Following twelve in the duodecimal system
The number names are no longer cardinal.
They are called ordinal numbers, which are produced
By combining one, two, or three with ten:
Thir-teen, four-teen, fif-teen, etcetera,
Which are three-ten and four-ten, alliterated
In English, French, and German.
It is not until thirteen is reached
That the process of counting ordinally (three plus ten)
Is employed in the ordinal naming of numbers
Where numbers are communicable by sound.
There are, however, number systems
Based on other pragmatic considerations.
Roman numerals constituted
An exclusively visual method
Of tactilely scoring or scratching
Of a one-by-one exclusively "visual" experience.
When nonliterates were assigned
To counting items such as sheep,
They made one tactile scratch
For one visually experienced sheep,
And a second tactile scratch
As another sheep passed visually,
And another scratch
As the next sheep passed.
The scratch was not a number,
It was only a tactile reaction
To visual experience.
It was a one-by-one,
Tooth-by-tooth intergearing
Of two prime
Sensorially apprehending systems__
Those of touch and sight.
While literate you, in retrospect, could say
That you see three scratches,
That is reflexively occasioned
Because you have learned to see groups
And because you have
A sound word for a set of three;
But nonliterate Roman servants who were scoring
Did not have to have number words
To match with tactile one-by-one scratching
Their one-by-one visually experienced,
One-by-one passing-by sheep.
The man doing the scratching
Did not have to have
Any verbal number words or set concepts.
Those landlords, priests, bankers,
Or unsolicited "protection" furnishers
Who were interested
In trading, taxing, or extracting
Life-sustaining wealth__
As sheep or wheat productivity__
Alone were concerned
With the specific total numbers of scratches
And of the total sheep or bags of grain
The ignorant servants had scratchingly matched.
From these total numbers
They calculated how many sheep or bags
They could extract for their taxes
Or landlord's tithe,
Or protectionist's fee,
Or banker's "interest"
Without totally discouraging
The sheepherders' or farmers' efforts.
"Pays" means land.
The shepherds and farmers
Were known as pagans
Or paysants, peasants,
I.e., land-working illiterates.
Because the first millennium A.D.
Roman Empire dominating Mediterranean world
Was so pragmatically mastered
By landlords and their calculating priests,
It is in evidence
That the Roman numerals constituted only
A one-by-one scoring system
In which the V for five and X for ten
Were tactilely "sophisticated" supervisor's
Tallying or totaling check marks
Which graphically illustrated
Their thumb's angular jutting out
From the four parallel packed fingers
Or digits of the totaler's free hand.
On the other hand, the intellectually conceived Arabic
numerals
Were graphic symbols
For the named sets
Of spontaneously perceived number aggregates.
The Arabic numerals
Did not come into use in the Mediterranean world
Until 700 A.D.
This was a thousand years after the Greeks had developed
Their intellectually conceived geometry.
The 700 A.D. introduction of Arabic numerals
Into the knowledge-monopolized economic transactions
Of the ignorance-enweakening Roman Empire
And Mediterranean European world in general
Occurred under the so-called "practical" assumption
That the Arabic numerals were only
Economical "shorthand" symbols
For the Roman scratches.
To the nonliterate ninety-nine percent of society,
It was obviously much easier to make a "3" squiggle
Than to make three separate vertical scratch strokes.
But to the illiterate the symbols
Did not conjure forth a number name.
The earliest calculating machine
Is the Chinese-invented abacus.
It is an oblong wooden frame
Which is subdivided
Into a large rectilinear bottom
And small top rectilinear areas
By a horizontal wooden bar
Running parallel to the top of the frame.
The frame's interior space is further subdivided
By a dozen or more
Perpendicularly strung parallel wires
Or thin bamboo rods.
There are four beads
Strung loosely into each of the wires
Below the horizontal crossbar,
And one bead strung loosely
Above the bar on each wire.
Start use of the abacus
With all the beads at bottom
Of their compartments.
In this all-lowered condition,
The columns are all "empty."
To put the number one
Into the first column on the right,
The topmost of the bottom four beads
Is elevated to the horizontal mid-bar.
To put the number two,
Two bottom beads are elevated to this bar.
To put five into the first column,
Lower all four bottom beads
And elevate the top bead.
To enter nine, leave the top bead elevated
And push up four beads
In the bottom section
On the first right-hand wire.
To enter ten,
Lower all beads in the right-hand column
Both above and below the crossbar;
Now elevate one bead In the bottom section
Of the second column from the right.
The first two right-hand columns read
One and zero, respectively,
Which spells out "ten."
The totaling bead
With a value of five In the separate compartment
At the head of each column
Permitted the release to inactive positioning
At the bottom of their wires
Of the one-by-one elevated bead aggregates.
Lowering of all beads
Permitted "empty columns" to occur.
Moving of the tenness leftward
Permitted progressive positioning,
Which integrated or differentiated out
As multiplication or division.
To those familiar with its use,
The tactile-visual patterns
Of the bead positions of the abacus
Could be mentally re-envisioned, or recalled
And held as afterimage sets
In the image-ination,
Which could be mentally manipulated
As columns of so many beads
Which read out progressively
As successively adjacent columns
Of so many beads,
Which, when reaching fiveness,
Called for moving "up" the one bead
Of the totaling head-compartment set,
While releasing the previously aggregated
Lower four beads
To drop into their empty-column condition.
When an additional four beads
Were pushed upwardly in the column,
An additional fiveness accrued.
All the beads in the column were lowered,
And one was entered
On the bottom compartment
Of the next leftward column,
As the two columns now read as "ten."
It was easier to enter
Many columned numbers in the abacus
And to add to them
Multicolumned numbers.
This process then permitted
Multiplication and division as well.
When an abacus was lost overboard or in the sands,
The overseas or over-desert navigator
Could sketch a picture
Of the abacus in the sand
Or on a piece of wood
With its easily remembered columns.
These abacus picturers invented
The "arabic" or abacus numerals
To represent the content
Of the successive columnar content of beads.
Obviously this abacus column imagining
Called also for a symbol
To represent an empty column,
And that symbol became the cyphra__
Or in England, cypher,
Or in American, cipher,
Or what we symbolize as 0,
And much later renamed "zero"
To eliminate the ambiguity
Between the identity of the word cypher
With the word for secret codes
And the word for the empty number,
All of which mathematical abacus elaboration
Became known scoffingly as "abracadabra"
To the 99 percent nonliterate world society,
And to the temporal power leaders
Who feared its portent
As an insidious disrupter
Of their ignorance-fortified authority.
Because of its utterly pragmatic bias,
The Roman culture had no numerical concept
Of "nothing"
That corresponds to the abacus's empty column__
That is, the idea of "no sheep"
Was ridiculous. Humans cannot eat "no sheep."
When the Europeans first adopted the Arabic numerals
in 700 A.D.
As "shorthand" for Roman numeral aggregates,
They of course encountered the Arabic cypher,
But they had no thinkably identifiable experiences to
associate with it.
"Nothing" obviously lacked "value."
For this reason, the Mediterranean Europeans
Thought of the cypher only as a decoration
Signifying the end of a communication
In the way that we use the word "over"
In contemporary radio communication.
The cypher was just an end period,
Just a decorative terminal symbol.
It was not until 1200 A.D.
Or five hundred years later,
That the works of a Persian named Algorismi
Were translated into
Latin and introduced into Europe.
Algorismi lived in Carthage, North Africa.
He wrote the first treatise explaining
How the Arabic cypher functioned calculatively
By progressively moving leftward
The newly attained tenness
By elevating one bead at the bottom
Of the bottom section
Of the next leftwardly adjacent column in multiplication
And next rightwardly in division.
Thus complex computation could be effected
Which had been impossible with Roman numerals.
The Arabic cypher had been used
For several millenniums
In the computational manner,
First in the Orient,
Then in Babylon and Egypt.
But such calculations had never before been made
In the Roman Empire's Mediterranean world.
No matter how intuitively
A man might have felt
About the probable significance
Of the principle of leverage
Or about the science of falling bodies,
Previous to the knowledge
Of the cypher's capabilities to position numbers,
He could not compute
Their relative effectiveness values
Without "long" multiplication and division.
The introduction into Europe
Of the computational significance of the cypher
Was an epoch-initiating event
For it made it possible for anybody to calculate.
And this was the moment in which
For the first time
The Copernicuses and Tycho Brahes,
The Galileos and Newtons,
The Keplers and Leonardos
Had computational ability.
This broke asunder the Dark Ages
With intellectual enlightenment
Regarding the scientific foundations
And technological responsibilities
Of cosmic miracles,
Now all the more miraculous
As the everyday realizer
Of all humanity's innate capabilities.
When I first went to school in 1899,
The shopkeepers in my Massachusetts town asked me
If I had "learned to do my cyphers"
By which key word__"cypher"__
They as yet identified all mathematics.
Even in 1970
Accountants in India
Are known officially as "cypherists."
Tobias Dantzig, author of Number: The Language of Science,
Has traced the etymological history
Of the names for the numbers
In all the known languages of the Earth.
He finds the names for numbers all classifiable
As amongst the "oldest" known words.
Sir James Jeans said "Science is the attempt
To set in order the facts of experience."
Dantzig, being a good scientist,
Undertook to set in order
The experienced facts of the history
Of the language of number names.
He arranged them experimentally
In their respective ethnic language columns.
Juxtaposed in this way
We are provided with new historical insights.
For instance, we learn
That if we are confronted
With two numbers of different languages,
Words that we have never seen before,
And an authority assures us
That one of these words means "one"
And the other means "two,"
And we are then asked to guess
Which of them means "one"
And which means "two,"
We will be surprised to find
That we can tell easily which is which.
"One" in every language
Starts with a vowel__
Eins, un, odyn, unus, yet, ahed__
And has vowel sound emphasis,
While "two" always has a consonant sound in the front__
Duo, zwei, dva, nee, tnayn, and so forth,
And has a consonant sound emphasis.
For instance, the Irish-Gaelic
Whose ancestors were sea rovers
Say "an" for one and "do" for two.
These vowel-consonant relations
Hold through into the teens__
Eleven, twelve__in English
Onze, douze__in French
Elf, zwoelf__in German,
With vowels for "oneness"
And consonants for "twoness."
Despite the dissimilarity in different languages
For the names for the same experiences,
And despite the unknown origins of the concepts
From which all numbers but five were derived,
The whole array of names for the numbers
In different languages
Makes it perfectly clear
That the names given the numbers around the world
Grew from the same fundamental
Conceptioning and sound roots.
In view of the foregoing discovery,
We either have to say that some angels
Invented the names for numbers
And the phonetically soundable
Alphabetical letter symbols
With which to spell them
And wrote them on parchments
And air-dropped those number-name leaflets
All around the spherical world,
Thus teaching world-around people the same number names:
Or we have to say that the numbers were invented
By one-world-around-traveling people.
However, if we adopt the latter possibility,
It becomes obvious that no single generation of people
Could, within its lifetime,
Or, in fact, within many lifetimes
Travel all around the world on foot,
For the world's lands are islanded.
But one way humans could get around,
And in a relative hurry,
Was by "high-seas-keeping" sailboats.
It thus becomes intuitively logical
To assume that sailors discovered
And invented the numbers
And inculcated their use
All around the world.
The Polynesians, we know,
Sailed all over the Pacific.
They probably sailed
From there into the Atlantic and Indian oceans
By riding ever-west-toward-east "Roaring Forties"__
The Forty-South latitudes'
Ever-eastward-revolving
Waters and atmospheric winds
Which circle around the vast Antarctic continent.
The "Roaring Forties"
Constitute a gigantic hydraulic-pneumatic merry-go-round,
Which as demonstrated by
World-around single-handing sailors of the 1960s
Enables those who master its ferocious waters
To encircle the world
Within only a year's time.
The Magellans, Cooks, and Slocums
With slower vessels circumnavigated in two years,
In contradistinction to the absolute inability
To go all around the world on foot.
The circumnavigation of the one-ocean world
Which covers three-quarters of our planet
Makes it obvious that the names for numbers
Were conceived by the sailors.
As Magellan, Cook, and later Slocum
Came to the Tierra del Fuego islanders,
They were surrounded by the islanders,
Who lived by pillaging passing ships
And must have been doing so
Profitably for millenniums.
To explain their sustained generations
In an environment approximately devoid
Of favorable human survival,
Except by piracy and salvage
Of the world-around sailing vessels
Funneled through the narrow
And incredibly tumultuous
Waters of the Horn Running between Antarctica and South America,
With often daily occurring
One-hundred-feet high waves
Cresting at the height
Of ten-story buildings,
Their thousand-ton tops
Tumblingly sheared off to leeward
By hundred-miles-an-hour superhurricanes
Avoidance of whose worst ferocities
Could be accomplished by winding
Through the Strait of Magellan,
Whose fishtrap-like strategic enticement
Often lured Pacific-Atlantic sea traffic
Into those pirates' forlorn domain.
With eighty-five percent of Earth's dry land
And ninety percent of its people
Occupying and dwelling north of the Equator
In the northern, or land-dominant, hemisphere;
And with less than one-tenth of one percent of humanity
Dwelling in the southernmost half
Of the southern, or wave-dominated, Earth hemisphere,
There is more and more scientific evidence accruing
That sailors have been encircling the Earth
South of Good Hope,
North or south of Australia,
And through the Horn
Consciously and competently
For many thousands of millenniums
All unknown to the ninety-nine percent of humanity
That has been "rooted" locally To their dry-land livelihoods.
The European scholars of the last millennium
Have considered the Polynesians to be illiterate
And therefore intellectually inferior to Europeans
Because the Polynesians didn't have a written history
And used only a binary mathematics,
Or "congruence in modulo two."
The European scholars scoffed,
"The Polynesians can only count to two."
Since the Polynesians lived on the sea
And were naked,
Anything upon which they wrote
Could be washed overboard.
The Polynesians themselves
Often fell overboard.
They had no pockets
Nor any other means
Of retaining reminder devices
Or calculating and scribing instruments
Other than by rings
That could not slip off
From their fingers, ankles, wrists, and necks,
Or by comblike items
That were precariously
Tied into the hair on their heads
Or by rings piercing their ears and noses.
These sea people had to invent ways of calculating and
communicating
Principally by brain-rememberable pattern images.
They accomplished their rememberable patterns in sound,
They remembered them in chants.
With day after day of time to spend at sea
They learned to sing and repeat these chants.
Using the successive bow-to-stern,
Canoe and dugout, stiffing ribs and thwarts
Or rafters of their great rafts
As re-minders of successive generations of ancestors,
They methodically and recitationally recalled
The experiences en-chantingly taught to them
As a successive-generation,
Oral relay system
Specifically identified with the paired ancestral parents,
Represented by each pair of ship's ribs or rafters.
When they landed for long periods
They upside-downed their longboats
To provide dry-from-rain habitats.
(The word for "roof" in Japan
Also means "bottom of boat.")
Staying longer than the wood-life of their hulls,
They built long halls patterned after the hulls.
Each successive column and roof rafter
Corresponded with a rib of their long boat.
Gradually they came to carve
Each stout tree column's wood
To represent an ancestor's image.
Each opposing pair of parallel columns
Represented a pair of ancestors:
The male on the one hand
And the female on the other hand.
While most Europeans or Americans can recall
Only ten or less generations of ancestors,
In their chants
The Polynesians can recall
As much as one hundred generations
Of paired ancestors,
And their chants include
The history of their important discoveries
Such as of specific-star-to-specific-star directions
to be followed at sea
In order to navigate from here to there.
While many of the words
That their ancestors evolved
To describe their discoveries
Have lost present-day identification,
They continue to sing these words
In faithful confidence
That their significant meaning
Will some day emerge.
Therefore, they teach their children
As they themselves were taught__
To chant successively the special stories
Which include words of lost meaning__
Describing each one of every pair of ancestors.
That is why the Vikings
Had their chants and sagas
And why sailors all around the world
Chant their chanties__"shanties"
As they heave-hoed rhythmically together.
Thus too did the Viking sing their sagas;
And the Japanese and Indian sailors their ragas;
And the Balinese sailors their gagas,
Meaning "tales of the old people,"
Amongst all those high-seas-living world dwellers
Whose single language structure
Served the thirty-million-square-mile living Maoris;
Whereas hundreds of fundamentally different languages
Were of static-existence necessity developed,
For instance, by isolatedly living tribes
Of exclusively inland-dwelling New Guineans.
A nineteenth-century sailor's shanty goes
"One, two, three, four
Sometimes I wish there were more.
Eins, zwei, drei, vier
I love the one that's near.
Yet, nee, same, see
So says the heathen Chinese.
Fair girls bereft
Then will get left
One, two, and three."
As complex twentieth-century,
Electronically actuated computers
Have come into use,
Ever improving methodology
For gaining greater use advantage
Of the computers' capabilities,
As information storing,
Retrieving, and interprocessing devices,
Has induced reassessment
Of relative mathematical systems' efficiencies.
This in turn has induced
Scientific discovery
That binary computation
Or operation by "congruence in modulo two"
Is by far the most efficient and swift system
For dealing universally with complex computation.
In this connection we recall that the Phoenicians
Also as sailor people
Were forced to keep their mercantile records
And recollections in sound patterns,
In contradistinction to tactile and visual scratching__
And that the Phoenicians to implement
Their world-around trading
Invented the Phoenician,
Or Phonetic, or word-sound alphabet,
With which to correlate and record graphically
The various sound patterns and pronunciations
Of the dialects they encountered In their world-around
trading.
And we suddenly realize
How brilliant and conceptually advanced
Were the Phoenicians' high-seas predecessors,
The Polynesians,
For the latter had long centuries earlier
Discovered the binary system of mathematics
Whose "congruence in modulo two"
Provided unambiguous,
Yes-no; go-no go,
Cybernetic controls
Of the electronic circuitry
For the modern computer,
As it had for millenniums earlier
Functioned most efficiently
In storing and retrieving
All the special-case data
In the brains of the Polynesians
By their chanted programming
And their persistent retention
Of the specific but no-longer-comprehended
Sound pattern words and sequences
Taught by their successive
Go-no go, male-female pairs of ancestors.
This realization forces rejection of the European scholars'
Former depreciation of the Polynesian competence,
Which reversal is typical
In both conceptioning and logic
Of the myriad of concept reversals
That are now taking place
And are about to occur
In vastly greater degree
In the late twentieth-century academic world.
The general education system
Has not yet formally acknowledged
The wholesale devaluation
Of their formally held
"Scholarly opinions and hypotheses,"
But that devaluation
Is indeed taking place
And is powerfully manifest
In the students' loss of esteem
For their intellectual wares.
All of the foregoing
Newly dawning realizations
Point up the significance
Of the world-around physically cross-bred kinship
Of the world's "one-ocean" sailors
Whose Atlantic, Pacific, and Indian waters
Were powerfully interconnected
By the Antarctic-encircling
"Roaring Forties."
Polynesians, Phoenicians, Venetians, Frisians, Vikings
(Pronounced "Veekings" by the Vikings)
All alliterations of the same words.
All evolved from the same ancestors.
The sea was their normal life,
And since three-quarters of the Earth's surface
Is covered with water,
"Normal" life would mean living on the sea.
The Polynesians spontaneously conceive of an island
As a "hole" in the ocean.
Such conceptioning of a negative hole in experience
Brought about their natural invention
Of a symbol for nothing__the zero.
This is negative space conceptioning
And is evident in the Maori paintings.
What is a peninsula to land people
Is a "bay" to them.
The Maori also look at males and females
In the reverse primacy of the land-stranded Western
culture.
Seventy-five percent of the planet is covered by the sea.
The sea is normal.
The male is the sailor.
The male is normal.
The penis of the normal sea
Intrudes into the female land.
The bay is a penis of the sea.
The females dwell upon the land.
To the landsman the peninsula or penis
Juts out into the ocean.
On the Indian Ocean side of southeast Africa,
The Zulus are linked with this round-the-world water
sailing.
They are probably evolved from the Polynesians of long
ago
Swept westward by the monsoons.
I found some of the Zulu chiefs
Wearing discs in their ears
Upon which the cardinal points of the compass
Were clearly marked.
The "Long Ears" of Easter Island
Had their ears pierced and stretched
To accommodate their navigational devices.
Many of the items which European society
Has misidentified in the Fijis as superstitious decoration
Were and as yet are
Navigational information-storing devices,
Being stored, for instance,
As star-pattern combs in their hair,
As rings around their necks,
Or as multiple bracelets
Mounted on their two arms and two legs,
And multiple rings
Upon the four fingers of their hands.
They had thirteen columns of slidable counters,
One neck, eight fingers, two arms, two legs.
Most of the earliest known abacuses
Also have thirteen columns of ring (bead) counters
Which became more convenient to manipulate and retain
When rib-bellied ships
Supplanted the open raft and catamaran.
Once the mathematical conceptioning
Of sliding rings on thirteen columns
Had been evolved by the navigators, traders, magicians,
It was no trick at all
To reproduce the thirteen-column system
In a wooden frame with bamboo slide columns.
By virtue of their ability to go
From the known here to the popularly unknown there,
The navigators were able to psychologically control
Their local island chieftains.
If a chieftain needed a miracle
To offset diminishing credit by his people,
He could confront them with his divine power
By exhibiting some object they had never seen before,
Because it was nonexistent
On their particular island.
All the chieftain had to do
Was to ask the navigators
To exercise their mysterious ability
To disappear at sea
And return days later with an unfamiliar object.
But the navigators kept secret
Their mathematical knowledge
Of offshore celestial navigation
And the lands they thus were able to reach.
To the landed chieftains
The seagoing navigators were mysterious priests.
The South Seas navigators lived and as yet live
Absolutely apart from the chieftains and the tribe
The "priests" taught only their sons about navigation
And they did so only at sea.
A new era dawned
For humanity on our planet
When the Polynesians learned
How to sail zigzaggingly to windward
Into the prevailing west-to-east winds.
Able to sail westward__
Able to follow the Sun__
At far greater sustainable
(All day and all night, day after day)
Sailing speeds than those attainable
By paddling or rowing into head seas;
Having for all time theretofore drifted
In predominantly eastward windblown directions,
Or gone aimlessly where ocean currents bore them,
Yielding to the inevitable
From-west-to-east elements
Bearing them to the American west coasts
And to all the Pacific islands
Throughout the previous x millions of years.
Whereas the Southern Hemisphere ocean
Was dominated by the west-east "Roaring Forties,"
The Polynesians when entering the Northern Hemisphere
Were advantaged not only by their ability
To sail into the wind,
But also by the east-west counter-currents
Of the tropical westward trade winds,
Which they discovered and
Called so because they made it possible
To go back where man had previously been
And thus to integrate world resources.
Thus the secretly held navigational capability
And knowledge of the elemental counting and astronomy
Went westward from Polynesia
Throughout Malaysia and to southern India,
Across the Indian Ocean to Mesopotamia and Egypt
And thence into the Mediterranean.
The powerful priests of Babylon, Egypt, and Crete
Were the progeny of mathematician navigators of the Pacific
Come up upon the land
To guide and miracle-ize the new kings
Of the Western Worlds.
Knowing all about boats,
These navigator priests were the only people
Who knew that the Earth is spherical,
That the Earth is a closed system
With its myriad resources chartable.
But being water people,
They kept their charts in their heads
And relayed the information
To their navigator progeny
Exclusively in esoterical,
Legendary, symbolical codings
Embroidered into their chants.
But some of their numbers
Also sailed deliberately eastward
Carrying their mathematical skills
To west-coast America.
The Mayans used base twenty in their numerical system
By counting with both their fingers and toes.
The number twenty often occurs
In a "magically" strategic way.
For an example
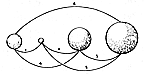
We can look at symmetrical aggregates
Of progressively assembled spheres
Closest packed on a plane__a pool table.
First take two balls and make them tangent.
Tangent is the "closest"
That spheres may come to one another.
We may next nest a third ball
In the valley between the first tangent two.
Now each of the three spheres is tangent to two others
And none can get closer to each other.
These three make a triangle.
There is no ball in the center
Of the triangular group.
We can now add three more balls to the first three
By arranging them tangentially in a row
Along one edge of the first three's triangle.
As yet, all six balls are arranged
As outside edges of the triangle.
Not until we add a fourth row of balls
Nested along one edge of the triangular aggregate
Does a single ball become placed as the nuclear ball
In the center of the triangular "patterned" ball pool-table array.
Ten is the total number of balls
In this first nuclear-ball-containing triangle:
Nine surround the nuclear tenth ball.
And since a triangle is a fundamental structural pattern,
And since the triangular aggregate
Of nine balls around a nuclear one
Is a symmetrical array,
Man's intuitive choice of "congruence in modulo ten"
May have been more subtly conceived
Than simply by coincidence
With the ten digits of his hands.
We will now see what happens experimentally
When sailors stack coconut or orange cargoes
Or when we stack planar groups of triangular aggregates of spheres
On top of one another in such a manner that they will be
Structurally stable without binding agents.
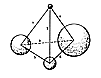
First we will nest six balls
In a closest-packed triangular planar array
On top of the first triangularly arranged ten-ball aggregate.
And on top of those six balls
We can nest three more.
We now have a total of nineteen balls.
We may now nest one more topmost ball
In the one "nest" of the three-ball triangle.
We now have a symmetrical
Tetrahedral aggregate
Consisting of twenty balls
Without any nuclear ball
Occurring in the center
Of the symmetrical tetrahedral pyramid of balls.
We began our vertical stacking
With a symmetrical base triangle of ten balls,
And now we have a tetrahedron composed of twenty balls.
Just as fingers alone may not have been the only reason
For the choice of base ten,
Fingers and toes together may not have been the only reason
That the Mayan priests chose
Congruence in modulo twenty
Or that twenty was considered a magical number.
It might have been the result of an intuitive understanding
Of closest packing of spheres,
Which is something much more fundamental.
For unlike our fingers which lie in a row,
The packing of twenty spheres
That can be grouped symmetrically together without a nucleus
Is a fundamentally significant phenomenon.
In a tetrahedron composed of twenty balls
There is no nucleus.
This may be why twenty appears so abundantly
In the different chemical element isotopes.
And "twenty" is one of the "Magic Numbers"
In the inventory of chemical-element isotopal abundancy in Universe.
In order to position a nuclear ball in the center
Of a symmetrical tetrahedral pyramid of balls,
We need to add another or fifth nested layer of fifteen
balls
To one face of the tetrahedron of twenty.
The total number of balls is then thirty-five,
Of which one is the nuclear ball.
If, however, we add four
Progressively larger
Triangular layers of balls
To each of the four triangular faces
Of the twenty-ball, no-nucleus tetrahedron,
It will take exactly one hundred more balls
To enclose the twenty-ball, no-nucleus tetrahedron__
This makes a symmetrical tetrahedron
Of one hundred and twenty balls.
This symmetrical tetrahedron
Is the largest symmetrical assembly
Of closest-packed spheres nowhere containing
Any two-layer-covered nuclear spheres
That is experimentally demonstrable.
In the external affairs of spheres
Such omnidimensional spherical groupings
Of one hundred and twenty same-size balls
Without a nucleus ball
Can be logically identified
With the internal affairs
Of individual spheres,
Wherein we rediscovered
The one hundred and twenty,
Least-common-denominator,
Right spherical triangles of the sphere,
Which are archeologically documented
As having been well known to the Babylonians'
Come-out-upon-the-land-ocean,
Navigator-high-priest mathematicians.
The number 120 also appears as a "Magic Number"
In the relative-abundance hierarchy
Of chemical-element isotopes of Universe.
One hundred and twenty accommodates
Both the decimal and the duodecimal system
(Ten multiplied by twelve).
The Mayans too may have understood
About the tetrahedral closest packing of spheres.
They probably made such tetrahedra
With symmetrically closest-packed stacks of oranges.
The twentieth-century fruit-store man
Spontaneously stacks his spherical fruits
In such closest-packed
Stacking and nesting arrays.
But the physicists didn't pay any attention
To the fruit-store man until 1922.
Then for the first time physicists
Called the tetrahedral stacks of fruit
"Closest packing of spheres."
For centuries past
The numerologists had paid attention
To the closest packing of spheres In tetrahedral pyramids,
But were given the academic heave-ho
When in the mid-nineteenth century
Physicists abandoned the concept of models.
We have seen
That there are unique or cardinal names
For the concepts one through twelve
In England and Germany,
And for the concepts one through sixteen in France,
But that after that they simply repeat
In whatever congruence modulos
They happen to be working.
The Arabic numerals as well as their names
Are unique and stand alone
Only from zero through nine.
However, eleven is the result of two ones__11,
And twelve is similarly fashioned from two
Previously given symbols,
Namely, one and two__12.
But certain numbers
Such as prime numbers
Have their own cosmic integrity
And therefore ought to be integrally expressed.
What the numerologist does
Is to add numerals horizontally (120=1+2+0=3)
Until they are all consolidated into one integer.
Numerologists have also assigned
To the letters of the alphabet
Corresponding numbers: A is one, B is two, C is three, etc.
Numerologists wishfully assume
That they can identify
Characteristics of people
By the residual integer
Derived from integrating
All of the integers,
(Which integers
They speak of as digits,
Identifying with the fingers of their hands,
That is, their fingers.)
Corresponding to all the letters
In the individual's complete set of names.
Numerologists do not pretend to be scientific.
They are just fascinated
With correspondence of their key digits
With various happenstances of existence.
They have great fun
Identifying events and things
And assuming significant insights
Which from time to time
Seem well justified,
But what games numerologists
Chose to play with these tools
May or may not have been significant.
Possibly by coincidence, however,
And possibly because of number integrity itself
Some of the integer intergrating results
Are found to correspond elegantly
With experimentally proven, physical laws
And have subsequently proven to be
Infinitely reliable.
Half a century ago I became interested in seeing
How numerologists played their games.
I found myself increasingly intrigued
And continually integrating digits.
|