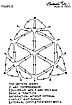
|
1107.30 
Persistence of Perpendicularity: As the frequency of
uniform spacing of
the rods increases and as the ends are uniformly and
infinitely extended, the distance each
end must move to accomplish union is infinitely decreased.
As this union takes place and
the surface of the original triangle becomes a spherical-surface
triangle of infinitely small
dimension on an infinitely large sphere, the chords
between the points of intersection of
the rods' triangle's surface, and the arcs between the
points of intersection, approach
infinitely negligible difference. We discern that, while
at the inflection point, the rods are at
right angles to the chord-arc__''negligible"__mean; that
they are not at right angles to the
chord at the gathering-of-the-ends phase; and that they
are always perpendicular to the
mean-arc-chord "infinity"; and that the condition of
perpendicularity is persistent
throughout all the transformation phases. Perpendicularity
does not "disappear" at the
zero-inflection phase of inside-outing, or positive-to-negative
transformation.
|
