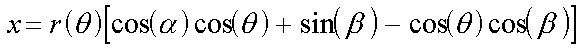 |
(1) |
 |
(2) |
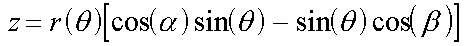 |
(3) |
I will give here some equations that will let you draw the pattern in any of its "breathing" positions. These equations will allow you to do various analysis of the pattern. (Future web pages will detail the results of some analysis already underway.)
Check out Lou Kauffman's web pages for more information about knots and about the Pattern Knot. Lou provides other equations.
To understand and use the following equations, you should realize that I have divided the pattern up into 4 arcs. If you do not understand this, see the section on constructing the pattern using a tetrahedron and the section on the pattern's relation to the octahedron. Each of the 4 arcs cover an angular range given by the range of the parameter alpha and is rotated above (or below) the xy-plane by the angular amount theta.
Also, these equations result in the pattern's arcs passing through each other. In a "real" knot the arcs would pass over or under one another, not through one another. (This might be avoided by making the radius depend on the parameter alpha.)
The equations are as follows:
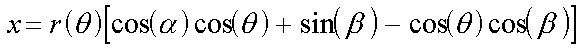 |
(1) |
 |
(2) |
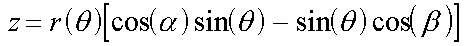 |
(3) |
where
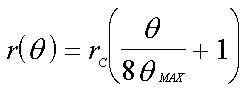 |
(4) |
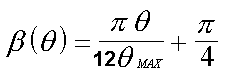 |
(5) |
In equation (4), r-sub-c is the radius of the arcs when the pattern is in its closed position.
The angle theta,
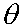 ,
gives the angle (amount) that the "pattern" is open.
The maximum value for the theta angle is 1/2 of the
dihedral angle of the octahedron.
,
gives the angle (amount) that the "pattern" is open.
The maximum value for the theta angle is 1/2 of the
dihedral angle of the octahedron.
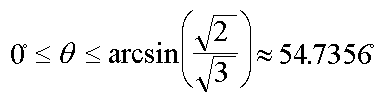 |
(6) |
With theta fixed, the arc angle alpha is given by
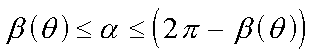 |
(7) |
These equations and angular ranges give you only 1 out of 4 of the pattern's arcs. To get the other 3 arcs make the following coordinate transformations.
| Arc #1 | Arc #2 | Arc #3 | Arc #4 | |
|---|---|---|---|---|
| x | x | -x | y | -y |
| y | y | y | -x | x |
| z | z | z | -z | -z |
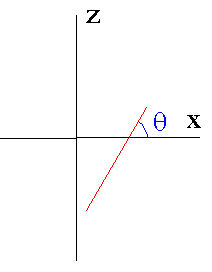
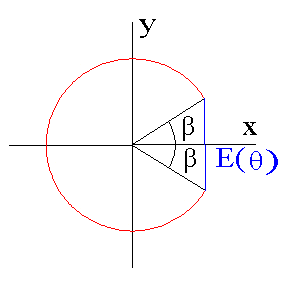
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.