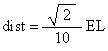We calculate the distance from the Tetrahedronís center of volume (COV) to a Tetrahelix symmetry axis passing through the Tetrahedron.
On another web page ( see here ) we calculated the vertex coordinates of a Tetrahedron when part of the Tetrahelix, with the condition that the edge length of the Tetrahedron EL=1, and that one vertex of the Tetrahedron is along the x-axis. We aligned the symmetry axis of the Tetrahelix so that it is the z-axis. The four (x, y, z) coordinates of the Tetrahedron are then given by
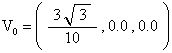
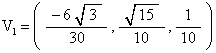
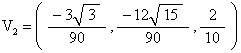
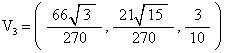
COV is calculated to be the average of these vertex coordinates. We get
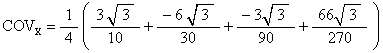
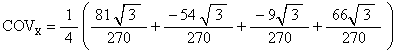
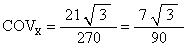
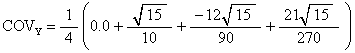
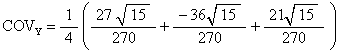
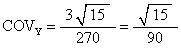
It doesnít matter what the z-component is because we want to know the distance from the z-axis to the COV, which is independent of the z-component. But we calculate it anyway.
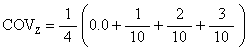
![]()
The distance from COV = (COVX, COVY, COVZ) to the z-axis is given by
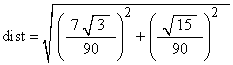
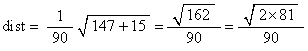
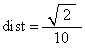
When the edge length (EL) is not equal to one, this becomes