450.00 Great Circles of the Vector Equilibrium and Icosahedron

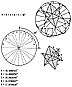Fig. 450.10

450.10 Great Circles of the Vector Equilibrium

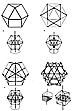Fig. 450.11A 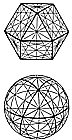Fig. 450.11B

450.11 Four Sets of Axes of Spin: The omni-equi-edged and radiused vector equilibrium is omnisymmetrical, having 12 vertexes, six square faces, eight triangular faces, and 24 edges for a total of 50 symmetrically positioned topological features. These four sets of unique topological aspects of the vector equilibrium provide four different sets of symmetrically positioned polar axes of spin to generate the 25 great circles of the vector equilibrium. The 25 great circles of the vector equilibrium are the equators of spin of the 25 axes of the 50 unique symmetrically positioned topological aspects of the vector equilibrium.

450.12 Six of the faces of the vector equilibrium are square, and they are only cornerjoined and symmetrically arrayed around the vector equilibrium in respect to one another. We can pair the six opposite square faces so that there are three pairs, and we can interconnect their opposite centers of area to provide three axes, corresponding to the XYZ coordinates of Cartesian geometry. We can spin the vector equilibrium on each of these three intersymmetrically positioned axes of square symmetry to produce three equators of spin. These axes generate the set of three intersymmetrical great-circle equators of the vector equilibrium. Together the three great circles subdivide the vector equilibrium into eight octants.

450.13 There are also eight symmetrically arrayed triangular faces of the vector equilibrium. We can pair the symmetrically opposite triangular faces so that there are four pairs, and we can interconnect their opposite centers of area to provide four intersymmetrically positioned axes. We can spin the vector equilibrium on each of these four axes of symmetry to produce four intersymmetrical equators of spin. These axes generate the set four intersymmetrical great-circle equators of the vector equilibrium.

450.14 When the 12 intersymmetrically positioned vertexes of the vector equilibrium are polarly interconnected, the lines of most economical interconnection provide six symmetrically interpositioned axes of spin. These six axes generate the set of six intersymmetrical great-circle equators of the vector equilibrium.

450.15 We may also most economically interconnect the 24 polarly opposed midpoints of the 24 intersymmetrically arrayed edges of the vector equilibrium to provide 12 sets of intersymmetrically positioned axes of spin. These axes generate the set of twelve intersymmetrical great-circle equators of the vector equilibrium.

450.16 As described, we now have sum-totally three square-face-centered axes, plus four triangular-face-centered axes, plus six vertex-centered axes, plus 12 edge-centered axes (3 + 4 + 6 + 12 = 25). There are a total of 25 complexedly intersymmetrical great circles of the vector equilibrium.

451.00 Vector Equilibrium: Axes of Symmetryand Points of Tangency in Closest Packing of Spheres

451.01 It is a characteristic of all the 25 great circles that each one of them goes through two or more of the vector equilibrium's 12 vertexes. Four of the great circles go through six vertexes; three of them go through four vertexes; and 18 of them go through two vertexes.

451.02 We find that all the sets of the great circles that can be generated by all the axes of symmetry of the vector equilibrium go through the 12 vertexes, which coincidentally constitute the only points of tangency of closestpacked, uniform-radius spheres. In omnidirectional closest packing, we always have 12 balls around one. The volumetric centers of the 12 uniformradius balls closest packed around one nuclear ball are congruent with the 12 vertexes of the vector equilibrium of twice the radius of the closest-packed spheres.

451.03 The network of vectorial lines most economically interconnecting the volumetric centers of 12 spheres closest packed around one nuclear sphere of the same radius describes not only the 24 external chords and 12 radii of the vector equilibrium but further outward extensions of the system by closest packing of additional uniform-radius spheres omnisurrounding the 12 spheres already closest packed around one sphere and most economically interconnecting each sphere with its 12 closest-packed tangential neighbors, altogether providing an isotropic vector matrix, i.e., an omnidirectional complex of vec torial lines all of the same length and all interconnected at identically angled convergences. Such an isotropic vector matrix is comprised internally entirely of triangular-faced, congruent, equiedged, equiangled octahedra and tetrahedra. This isotropic matrix constitues the omnidirectional grid.

451.04 The basic gridding employed by nature is the most economical agglomeration of the atoms of any one element. We find nature time and again using this closest packing for most economical energy coordinations.

452.00 Vector Equilibrium: Great-Circle Railroad Tracks of Energy

452.01 The 12 points of tangency of unit-radius spheres in closest packing, such as is employed by any given chemical element, are important because energies traveling over the surface of spheres must follow the most economical spherical surface routes, which are inherently great circle routes, and in order to travel over a series of spheres, they could pass from one sphere to another only at the 12 points of tangency of any one sphere with its closestpacked neighboring uniform-radius sphere.

452.02 The vector equilibrium's 25 great circles, all of which pass through the 12 vertexes, represent the only "most economical lines" of energy travel from one sphere to another. The 25 great circles constitute all the possible "most economical railroad tracks" of energy travel from one atom to another of the same chemical elements. Energy can and does travel from sphere to sphere of closest-packed sphere agglomerations only by following the 25 surface great circles of the vector equilibrium, always accomplishing the most economical travel distances through the only 12 points of closestpacked tangency.

452.03 If we stretch an initially flat rubber sheet around a sphere, the outer spherical surface is stretched further than the inside spherical surface of the same rubber sheet simply because circumference increases with radial increase, and the more tensed side of the sheet has its atoms pulled into closerradial proximity to one another. Electromagnetic energy follows the most highly tensioned, ergo the most atomically dense, metallic element regions, wherefore it always follows great-circle patterns on the convex surface of metallic spheres. Large copper-shelled spheres called Van De Graaff electrostatic generators are employed as electrical charge accumulators. As much as two million volts may be accumulated on one sphere's surface, ultimately to be discharged in a lightninglike leap- across to a near neighbor copper sphere. While a small fraction of this voltage might electrocute humans, people may walk around inside such high-voltage-charged spheres with impunity because the electric energy will never follow the concave surface paths but only the outer convex great-circle paths for, by kinetic inherency, they will always follow the great-circle paths of greatest radius.

452.04 You could be the little man in Universe who always goes from sphere to sphere through the points of intersphere tangencies. If you lived inside the concave surface of one sphere, you could go through the point of tangency into the next sphere, and you could go right through Universe that way always inside spheres. Or you could be the little man who lives on the outside of the spheres, always living convexly, and when you came to the point of tangency with the next sphere, you could go on to that next sphere convexly, and you could go right through Universe that way. Concave is one way of looking at Universe, and convex is another. Both are equally valid and cosmically extensive. This is typical of how we should not be fooled when we look at spheres __or by just looking at the little local triangle on the surface of our big sphere and missing the big triangle6 always polarly complementing it and defined by the same three edges but consisting of all the unit spherical surface area on the outer side of the small triangle's three edges. These concave-convex, inside-out, and surface-area complementations are beginning to give us new clues to conceptual comprehending.

(Footnote 6: See Sec. 810, "One Spherical Triangle Considered as Four.")

452.05 As was theoretically indicated in the foregoing energy-path discoveries, we confirm experimentally that electric charges never travel on the concave side of a sphere: they always stay on the convex surface. In the phenomenon of electroplating, the convex surfaces are readily treated while it is almost impossible to plate the concave side except by use of a close matrix of local spots. The convex side goes into higher tension, which means that it is stretched thinner and tauter and is not only less travel-resistant, but is more readily conductive because its atoms are closer to one another. This means that electromagnetic energy automatically follows around the outside of convex surfaces. It is experimentally disclosed and confirmed that energy always seeks the most economical, ergo shortest, routes of travel. And we have seen See Sec. 810, "One Spherical Triangle Considered as Four." that the shortest intersphere or interatom routes consist exclusively of the 25 great-circle geodesic-surface routes, which transit the 12 vertexes of the vector equilibrium, and which thus transit all the possible points of tangency of closest-packed spheres.

452.06 There always exists some gap between the closest-packed spheres due to the nuclear kinetics and absolute discontinuity of all particulate matter. When the 12 tangency gaps are widened beyond voltage jumpability, the eternally regenerative conservation of cosmic energy by pure generalized principles will reroute the energies on spherically closed great-circle "holding patterns" of the 25 great circles, which are those produced by the central-angle foldings of the four unique great-circle sets altogether comprising the vector equilibrium's 25 great circles.

452.07 High energy charges in energy networks refuse to take the longest of the two great-circle arc routes existing between any two spherical points. Energy always tends to "short-circuit," that is, to complete the circuit between any two spherical surface points by the shortest great-circle arc route. This means that energy automatically triangulates via the diagonal of a square or via the triangulating diagonals of any other polygons to which force is applied. Triangular systems represent the shortest, most economical energy networks. The triangle constitutes the self-stabilizing pattern of complex kinetic energy interference occasioned angular shuntings and three-fold or more circle interaction averaging of least-resistant directional resultants, which always trend toward equiangular configurations, whether occurring as free radiant energy events or as local self- structurings.