800.00 Operational Mathematics

801.00 Sensoriality: Sweepout

801.01 Alternate Faculties of Sensation

801.02 Information is experience. Experience is information. We have all experienced the information given to us directly through our own sensing faculties or relayed to us by others through our sensing faculties, but as originally sensed directly by others and not by ourselves. The only way that we know that we "are," that we are alive in Universe, is through information apprehended by our own sensorial faculties. We can hear, see, taste, smell, and touch-feel. We have all experienced the information-relaying relationships between the old life and the new life. The old life is excited to see how early the new life develops, coordinates, and responds both consciously to external information and subconsciously to internally programmed instructions of the brain or of the genes. The old life tries to speed the development of the new life's communicated comprehending by pointing to first the child's and then the "old life" speaker's eye and saying, "eye, eye, eye," "mouth, mouth, mouth," and "ear, ear, ear," while pointing to those instruments until the child responds by making a similar sound. However, it is seldom that we observe parents thus engaged with their children refer to their internal organs, such as the endocrine glands. In fact, parents may not even know of these glands, let alone where they are situated. Such word-coaching by oldsters of youngsters relies almost exclusively upon identification of superficial characteristics and comprehends only in superficial degree those organs to which they refer.

801.03 Let us imagine a scientifically conducted experiment designed to disclose the unique behavioral characteristics of each of those four prime sensing faculties without which we could not apprehend Universe and could not have sense of being.

801.04 Let us suppose that you are blindfolded and that your mouth, nostrils, and ears are also simultaneously bound closed. Only your tactile sensing is operative. To find out about yourself and local Universe, you would begin by reaching out around you with your arms-extended hands. You could learn environmental conditions through your hands. You could lean forward, and the sense of balance would tell you how far you can reach without shifting your base position. You discover that you are prospecting with your sensitive skin terminals, as does an insect with all its radially and circumferentially orientable feelers. Your most extreme and mobile skin feelers are your toes and your fingers. You are trying to get terminal reach information before you move on from your safe base. You will not risk shifting your weight until you are certain that you will be supported. You will not move into a place so small you cannot turn around and escape. Without changing your base, and standing with all your weight on your left foot, you learn that you can stretch out and sweep out with your arms while at the same time sweeping space and testing the ground's firmness with your right leg. Thus you learn that there is a maximum range of information gathering, which is the distance between the right foot's big toe and your left hand's middle fingertip. Most of us have a toe-to-fingertip reach of about six or eight feet. In these sense-limited conditions, our only way of finding out about Universe is tactile, through touch alone. Very quickly, we become supersensitive with our feet and hands, particularly with our feet and legs in gravitational balancing. Every child learns this in summer while at camp. At home, his parents won't let him stay up after dark, but maybe at night he is very fond of a path that goes down to the water. He starts going on that path and finds himself running along in the dark. Even though you can't see, you remember well the pattern of turns, depressions, hills, and dales. Your feet feel familiar with the path; the rhythm of steps and heartbeats subconsciously monitors your memory- bank control of your running along that familiar path barefootedly in the dark. We find experimentally that we can remember patterns tactilely and feel very safe following them. We are even able to run back and forth over a local complex of familiar ground and we can run at about 10 miles per hour. Wherefore our static tactile information-gathering, which commands a maximum spherical range of 10 feet in diameter, is augmented by the 10-miles-per-hour dynamic range-minding capability.

801.05 Ecology is the science of cataloguing, ordering, and inspecting patterns of life. Different kinds of life demonstrate different patterns. There is a difference of radius of sweepout of wolves, seagulls, and man. If we humans had only the tactile sense to go by in our ecological patterning, we could only sweep out a fairly small territory, but we could get so used to it that we would probably run around in the known territory. (See Sec. 1005.20.)

801.06 But now suppose that you cover up all your skin and uncover your nostrils and your mouth. Your eyes and ears are still covered and your feet and hands are now tied down so you cannot move. You have only olfactory information. Under these conditions, men's measurements are governed by three factors: (1) the radius of the permeation of gases within gases; (2) the concentration and viscosity of such gases, such as orange groves, pine woods, and so forth; and (3) the wind. Men coming in from months at sea have smelled orange groves and pine trees at somewhere around a mile offshore in still air. Such gases remain sufficiently concentrated to be detectable at a mile. (Of course, dogs can smell at greater distances than our human standing-still olfactory range of about a mile.) If the wind is blowing, the velocity is enhanced so we get smoke from forest fires at great distances. In great, 400-miles-per-hour, high altitude, jet stream winds, the smellable concentration can persist to a range of even 100 miles. Whereas our tactile sense's static range is 10 feet, which equals about 1/500th of a mile; and its dynamic velocity range augmentation is 10 miles per hour, we find our olfactoral static range of information- gathering is 100 miles and its dynamic range is 400 miles per hour.

801.07 If we now shut off the mouth and nostrils__with eyes and skin also blanked out__and we then open up only the ears, we cannot see, smell, or feel; we have only sounds to reckon by. Men have heard sounds at very great distances. Sounds will bounce on the water, into the atmosphere, and back on the water again. Sound is a wave phenomenon that men have heard at ranges up to 100 miles, as in the case of the atomic bomb. The speed of sound in the air is about 700 miles per hour; the static hearing range is about 100 miles, while the dynamic hearing range is 1,100 miles per hour (700 m.p.h. + 400 m.p.h. jet-stream wind = 1,100 m.p.h.).

801.08 We next shut off the tactile, olfactory, and oral sensing, then uncover and open our eyes. Men see stars that are billions of miles away. We know the velocity of light is 186,000 miles per second, or about 700 million miles per hour. We find that the visual sensing is in an entirely different order of magnitude. The tactile, olfactory, and oral faculties as a group are so minuscule as compared to the range of the visual that they cannot even be considered together.

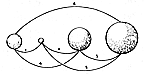
801.09 Human Sense Ranging and Information Gathering Radius of Static Ranging: Dynamic Velocity: Tactile 1/1,000th of a mile 10 miles per hour Olfactory 1 mile 400 miles per hour Aural 100 miles 1,100 miles per hour Visual 6,000,000,000,000,000,000 miles1 700,000,000 miles per hour If we try to plot two curves of these static and dynamic human sensing capabilities on a chart, we will have no trouble in positioning the first three senses; but to reach the point on the chart at which the sight capabilities occur, we will have to take an airplane and fly for many days to reach those positions. It is clear that as we recede from the first three sets of points, they will tend gradually to appear as one. This disparity has not been taught to us. We were told that our senses were approximately equal and alternate capabilities. Court imposed "damage costs" for their respective losses are approximately equal. We found out the disparity ourselves by examining the limit-case conditions, which can only be discovered by physical experience. This method of discovery is called "operational procedure." (Footnote 1: One light year is six trillion miles, and humans see Andromeda with the naked eye one million light years away, which means six quintillion miles.)

801.10 Sense Coordination of the Infant

801.11 One of the most surprising things about a newborn child is that it is already tactilely coordinated. Even in the first day, the baby is so well coordinated tactilely that if you put your finger against its palm, the baby will close its hand firmly and deftly around your finger, although it is not using its ears or eyes at all. If you will now exert a tiny bit of tension effort to remove your finger, the child will respond at once by opening its hand. The infant will repeat the closing and opening response to your initiatives as many times as you may wish to initiate. This should not surprise us if we realize that the baby has been in tactile communication with its mother for months before evacuating her womb, within which, however, its visual, olfactory, and aural faculties were muted and inoperative. Not much time after birth the child employs for the first time its olfactory glands and starts searching the mother's breast and the source of milk. Quite a few days later it begins to hear; and very much later, it sees. The sequence in which the child's faculties become employed corresponds to the order of increased range of its respective faculties of information apprehending.

801.12 Thus we find the child successively coordinating the first three faculties: the tactile, the olfactory, and the aural. He begins to learn how they work together and quite rapidly gets to be very skillful in coordinating and handling the information coming to him through these senses. It is only days later that he begins to use his sight. He tries tactilely, olfactorily, and aurally to confirm what he sees to be reality. He cannot do so over any great distance because neither his arms and hands nor his tasting mouth will reach very far. Months later, the child crawls to check tactilely, olfactorily, and aurally on phenomena still further away; and thereby to coordinatingly sort out his information inputs; and thereby develop a scheme of__and a total sense of__reality and repetitive event expectancy. He crawls over to the chair to find that his eyes have reported to him correctly that the chair is indeed there. He begins to check up and coordinate on more distant objects, and he finds his visual ability to be reliable. The child seeing the Fourth of July fireworks for the first time sees a flash and then hears a boom. Maybe that doesn't mean so much to him, because boom (aural) and flash (optical) may be different phenomena; but when he sees a man hammering a fence post, he has by this time been hammering a whole lot and he knows the sound that makes. He may not be very sure of the fireworks in the sky, the flash and the boom, but he is really very confident about the sound of the hammering of the fence post. When he sees the man hammer and then hears the sound a fraction later, he begins to realize that there is some lag in the rates in which he gets information from different faculties. His eye gets it faster than his ear.

801.13 The three postnatal senses the child coordinates are secondary. The first prenatal one, the tactile, is primary. The real emphasis of the judgment of life is on the tactile, the primary, the thing you can touch.2 The ranges of the first three senses are so close together, and sight is so different, that we may best rank them as #1, touch, being a primary set; with both #2, olfactoral coupled with #3, aural, as a secondary set; and #4 sight, as a tertiary set: wherefore in effect, touch is the yesterday set; while the olfactoral and aural (what you are smelling, eating, saying, and hearing) are the now set; while sight (what only may be next) is the future set. (We can seem to see, but we have not yet come to it.) Whereas reality is eternally now, human apprehending demonstrates a large assortment of lags in rates of cognitions whose myriadly multivaried frequencies of myriadly multivaried, positive-negative, omnidirectional aberrations, in multivaried degrees, produce such elusively off-center effects as possibly to result in an illusionary awareness of an approximately unlimited number of individually different awareness patterns, all of whose relative imperfections induce the illusion of a reality in which "life" is terminal, because physically imperfect; as contrasted to mind's discovery of an omni- interaccommodative complex of a variety of different a priori, cosmic, and eternal principles, which can only be intellectually discovered, have no weight, and apparently manifest a perfect, abstract, eternal design, the metaphysical utterly transcendent of the physical. (Footnote 2: You can reflect philosophically on some of the things touch does, like making people want to get their hands on the coin, the key, or whatever it may be.)

801.14 The 186,000-miles-per-second speed of light is so fast that it was only just recently measured, and it doesn't really have much meaning to us. You don't have a sense of 700 million miles per hour. If you did get to "see" that way, you would be spontaneously conscious of seeing the Sun eight minutes after the horizon had obscured it; ergo, consciously seeing an arc around the Earth's curvature. We are not seeing that way as yet. To explain our sight, we call it "instantaneous." We say we can see instantaneously. This fact has misled us very greatly. You insist that you are seeing the black-and-white page of this book, do you not? You're not. You have a brain-centered television set, and the light is bouncing off the page. The resultant comes back through your optical system and is scanned and actually goes back into the brain, and you are seeing the page in your brain. You are not seeing the page out in front of you. We have gotten used to the idea that we see outside of ourselves, but we just don't do so. It only takes about a billionth of a second for the light to bounce off the page and get in the brain to be scanned, so the child is fooled into thinking that he is seeing outside of himself. And we are misinforming ourselves in discounting the lag and assuming that we see it "over there." No one has ever seen outside themselves.

801.20 The Omnidirectional TV Set

801.21 Children looking at TV today look at it quite differently from the way it was to the first generation of TV adults. It begins to be very much a part of the child's life, and he tends to accredit it the way adults accredit what they get from their eyes. When children are looking at a baseball game, they are right there in the field. All of our vision operates as an omnidirectional TV set, and there is no way to escape it. That is all we have ever lived in. We have all been in omnidirectional TV sets all our lives, and we have gotten so accustomed to the reliability of the information that we have, in effect, projected ourselves into the field. We may insist that we see each other out in the field. But all vision actually operates inside the brain in organic, neuron-transistored TV sets.

801.22 We have all heard people describe other people, in a derogatory way, as being "full of imagination." The fact is that if you are not full of imagination, you are not very sane. All we do is deal in brain images. We traffic in the memory sets, the TV sets, the recall sets, and certain incoming sets. When you say that you see me or you say "I see you," or "I touch you," I am confining information about you to the "tactile you." If I had never had a tactile experience (which could easily be if I were paralyzed at conception), "you" might be only where I smell you. "You" would have only the smellable identity that we have for our dogs. You would be as big as you smell. Then, if I had never smelled, tasted, nor experienced tactile sensing, you would be strictly the hearable you.

801.23 What is really important, however, about you or me is the thinkable you or the thinkable me, the abstract metaphysical you or me, what we have done with these images, the relatedness we have found, what communications we have made with one another. We begin to realize that the dimensions of the thinkable you are phenomenal, when you hear Mozart on the radio, that is, the metaphysical__only intellectually identifiable__eternal Mozart who will always be there to any who hears his music. When we say "atom" or think "atom" we are intellect-to-intellect with livingly thinkable Democritus, who first conceived and named the invisible phenomenon "atom." Were exclusively tactile Democritus to be sitting next to you, surely you would not recognize him nor accredit him as you do the only-thinkable Democritus and what he thought about the atom. You say to me: "I see you sitting there." And all you see is a little of my pink face and hands and my shoes and clothing, and you can't see me, which is entirely the thinking, abstract, metaphysical me. It becomes shocking to think that we recognize one another only as the touchable, nonthinking biological organism and its clothed ensemble.

801.24 Reconsidered in these significant identification terms, there is quite a different significance in what we term "dead" as a strictly tactile "thing," in contrast to the exclusively "thinking" you or me. We can put the touchable things in the ground, but we can't put the thinking and thinkable you in the ground. The fact that I see you only as the touchable you keeps shocking me. The baby's spontaneous touching becomes the dominant sense measure, wherefore we insist on measuring the inches or the feet. We talk this way even though these are not the right increments. My exclusively tactile seeing inadequacy becomes a kind of warning, despite my only theoretical knowledge of the error of seeing you only as the touchable you. I keep spontaneously seeing the tactile living you. The tactile is very unreliable; it has little meaning. Though you know they are gentle, sweet children, when they put on Hallowe'en monster masks they "look" like monsters. It was precisely in this manner that human beings came to err in identifying life only with the touchable physical, which is exactly what life isn't. (See Sec. 531.)

810.00 One Spherical Triangle Considered as Four

811.00 Bias on One Side of the Line

811.01 We have all been brought up with a plane geometry in which a triangle was conceived and defined as an area bound by a closed line of three edges and three angles. A circle was an area bound by a closed line of unit radius. The area outside the closed boundary line was not only undefinable but was inconceivable and unconsidered.

811.02 In the abstract, ghostly geometry of the Greeks, the triangle and circle were inscribed in a plane that extended laterally to infinity. So tiny is man and so limited was man's experience that at the time of the Greeks, he had no notion that he was living on a planet. Man seemed obviously to be living on an intuitively expansive planar world around and above which passed the Sun and stars, after which they plunged into the sea and arose again in the morning. This cosmological concept of an eternally extended, planar-based Earth sandwiched between heaven above and hell below made infinity obvious, ergo axiomatic, to the Greeks.

811.03 The Greek geometers could not therefore define the planar extensibility that lay outside and beyond the line of known content. Since the surface outside of the line went to infinity, you could not include it in your computation. The Greeks' concept of the geometrical, bound-area of their triangle__or their circle__lay demonstrably on only one bound-area side of the line. As a consequence of such fundamental schooling, world society became historically biased about everything. Continually facing survival strategy choices, society assumed that it must always choose between two or more political or religious "sides." Thus developed the seeming nobility of loyalties. Society has been educated to look for logic and reliability only on one side of a line, hoping that the side chosen, on one hand or the other of indeterminately large lines, may be on the inside of the line. This logic is at the head of our reflexively conditioned biases. We are continually being pressed to validate one side of the line or the other.

811.04 You can "draw a line" only on the surface of some system. All systems divide Universe into insideness and outsideness. Systems are finite. Validity favors neither one side of the line nor the other. Every time we draw a line operationally upon a system, it returns upon itself. The line always divides a whole system's unit area surface into two areas, each equally valid as unit areas. Operational geometry invalidates all bias.

812.00 Spherical Triangle

812.01 The shortest distance between any two points on the surface of a sphere is always described by an arc of a great circle. A triangle drawn most economically on the Earth's surface or on the surface of any other sphere is actually always a spherical triangle described by great-circle arcs. The sum of the three angles of a spherical triangle is never 180 degrees. Spherical trigonometry is different from plane trigonometry; in the latter, the sum of any triangle's angles is always 180 degrees. There is no plane flat surface on Earth, wherefore no plane triangles can be demonstrated on its surface. Operationally speaking, we always deal in systems, and all systems are characterized projectionally by spherical triangles, which control all our experimental transformations.

812.02 Drawing or scribing is an operational term. It is impossible to draw without an object upon which to draw. The drawing may be by depositing on or by carving away__that is, by creating a trajectory or tracery of the operational event. All the objects upon which drawing may be operationally accomplished are structural systems having insideness and outsideness. The drawn-upon object may be either symmetrical or asymmetrical. A piece of paper or a blackboard is a system having insideness and outsideness.

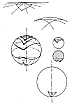Fig. 812.03

812.03 When we draw a triangle on the surface of Earth (which previously unscribed area was unit before the scribing or drawing), we divide Earth's surface into two areas on either side of the line. One may be a little local triangle whose three angles seem to add up to 180 degrees, while the other big spherical triangle complementing the small one to account together for all the Earth's surface has angles adding up to 900 degrees or less. This means that each corner of the big triangle complementing the small local one, with corners seeming to be only 60 degrees each, must be 300 degrees each, for there are approximately 360 degrees around each point on the surface of a sphere. Therefore the sum of all the three angles of the big Earth triangles, which inherently complement the little local 60-degree-per-corner equilateral triangles, must be 900 degrees. The big 900-degree triangle is also an area bounded by three lines and three angles. Our schooled-in bias renders it typical of us to miss the big triangle while being preoccupied only locally with the negligibly sized triangular area.

812.04 If you inscribe one triangle on a spherical system, you inevitably describe four triangles. There is a concave small triangle and a concave big triangle, as viewed from inside, and a convex small triangle and a convex big triangle, as viewed from outside. Concave and convex are not the same, so at minimum there always are inherently four triangles.

812.05 Background Nothingness: One spherical triangle ABC drawn on the Earth's surface inadvertently produces four triangles as the corners of the surface triangle are inherently related to the center of the Earth D, and their lines of interrelatedness together with the three edge lines of the surface triangle describe a tetrahedron. (See Fig. 812.03.) Drawing a triangle on the surface of the Earth (as described at Sec. 810) also divides the surface of the Earth into two areas__one large, one small__both of which are bound by a closed line with three edges and three angles. The large triangle and the small triangle have both concave and convex aspects__ergo, four triangles in all. Euler did not recognize the background nothingness of the outside triangles. (See Sec. 505.81.)

812.06 Under the most primitive pre-time-size conditions the surface of a sphere may be exactly subdivided into the four spherical triangles of the spherical tetrahedron, each of whose surface corners are 120-degree angles, and whose "edges" have central angles of 109 28'. The area of a surface of a sphere is also exactly equal to the area of four great circles of the sphere. Ergo, the area of a sphere's great circle equals the area of a spherical triangle of that sphere's spherical tetrahedron: wherefore we have a circular area exactly equaling a triangular area, and we have avoided use of pi .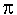

813.00 Square or Triangle Becomes Great Circle at Equator

813.01 If we draw a closed line such as a circle around Earth, it must divide its total unit surface into two areas, as does the equator divide Earth into southern and northern hemispheres. If we draw a lesser-sized circle on Earth, such as the circle of North latitude 70°, it divides Earth's total surface into a very large southern area and a relatively small northern area. If we go outdoors and draw a circle on the ground, it will divide the whole area of our planet Earth into two areas__one will be very small, the other very large.

813.02 If our little circle has an area of one square foot, the big circle has an area of approximately five quadrillion square feet, because our 8,000-mile-diameter Earth has an approximately 200-million-square-mile surface. Each square mile has approximately 25 million square feet, which, multiplied, gives a five followed by fifteen zeros: 5,000,000,000,000,000 square feet. This is written by the scientists as 5×1015 square feet; while compact, this tends to disconnect from our senses. Scientists have been forced to disconnect from our senses due to the errors of our senses, which we are now able to rectify. As we reconnect our senses with the reality of Universe, we begin to regain competent thinking by humans, and thereby possibly their continuance in Universe as competently functioning team members__members of the varsity or University team of Universe.

813.03 If, instead of drawing a one-square-foot circle on the ground__which means on the surface of the spherical Earth__we were to draw a square that is one foot on each side, we would have the same size local area as before: one square foot. A square as defined by Euclid is an area bound by a closed line of four equal-length edges and four equal and identical angles. By this definition, our little square, one foot to a side, that we have drawn on the ground is a closed line of four equal edges and equal angles. But this divides all Earth's surface into two areas, both of which are equally bound by four equal- length edges and four equal angles. Therefore, we have two squares: one little local one and one enormous one. And the little one's corners are approximately 90 degrees each, which makes the big square's corners approximately 270 degrees each. While you may not be familiar with such thinking, you are confronted with the results of a physical experiment, which inform you that you have been laboring under many debilitating illusions.

813.04 If you make your small square a little bigger and your bigger one a little smaller by increasing the little one's edges to one mile each, you will have a local one square mile__a customary unit of western United States ranches__and the big square will be approximately 199,999,999 square miles. As you further increase the size of the square, using great-circle lines, which are the shortest distances on a sphere between any two points, to draw the square's edges, you will find the small square's corner angles increasing while the big one's corner angles are decreasing. If you now make your square so that its area is one half that of the Earth, 100 million square miles, in order to have all your edges the same and all your angles the same, you will find that each of the corners of both squares is 180 degrees. That is to say, the edges of both squares lie along Earth's equator so that the areas of both are approximately 10 million square miles.

814.00 Complementarity of System Surfaces

814.01 The progressive enlargement of a triangle, a pentagon, an octagon, or any other equiedged, closed-line figure drawn on any system's surface produces similar results to that of the enlarging square with 180 degrees to each corner at the equator. The closed- line surface figure will always and only divide the whole area into two complementary areas. Each human making this discovery experimentally says spontaneously, "But I didn't mean to make the big triangle," or "the big square," or indeed, the big mess of pollution. This lack of intention in no way alters these truths of Universe. We are all equally responsible. We are responsible not only for the big complementary surface areas we develop on systems by our every act, but also for the finite, complementary outward tetrahedron automatically complementing and enclosing each system we devise. We are inherently responsible for the complementary transformation of Universe, inwardly, outwardly, and all around every system we alter.