456.00 Transformation of Vector Equilibrium into Icosahedron
456.01 While its vertical radii are uniformly contracted from the vector equilibrium's vertexial radii, the icosahedron's surface is simultaneously and symmetrically askewed from the vector equilibrium's surface symmetry. The vector equilibrium's eight triangles do not transform, but its six square faces transform into 12 additional triangles identical to the vector equilibrium's original eight, with five triangles cornered together at the same original 12 vertexes of the vector equilibrium.
456.02 The icosahedron's five-triangled vertexes have odd-number-imposed, inherent interangle bisectioning, that is, extensions of the 30 great circle edges of any of the icosahedron's 20 triangles automatically bisecting the apex angle of the adjacently intruded triangle into which it has passed. Thus extension of all the icosahedron's 20 triangles' 30 edges automatically bisects all of its original 60 vertexial-centered, equiangled 36-degree corners, with all the angle bisectors inherently impinging perpendicularly upon the opposite mid-edges of the icosahedron's 20 equilateral, equiangled 72-degreecornered triangles. The bisecting great-circle extensions from each of all three of the original 20 triangles' apexes cross inherently (as proven elsewhere in Euclidian geometry) at the areal center of those 20 original icosahedral triangles. Those perpendicular bisectors subdivide each of the original 20 equiangled triangles into six right-angled triangles, which multiplies the total surface subdivisioning into 120 "similar" right-angled triangles, 60 of which are positive and 60 of which are negative, whose corners in the spherical great-circle patterning are 90°, 60°, and 36°, respectively, and their chordally composed corresponding planar polyhedral triangles are 90, 60, and 30 degrees, respectively. There is exactly 6 degrees of "spherical excess," as it is formally known, between the 120 spherical vs. 120 planar triangles.
456.03 This positive-negative subdivision of the whole system puts half the system into negative phase and the other half into positive phase, which discloses an exclusively external "surface" positive-negative relationship quite apart from that of the two surface polar hemispheres. This new aspect of complementarity is similar to the systematic omnicoexistence of the concave and convex non-mirror-imaged complementarity whose concavity and convexity make the 60 positive and 60 negative surface triangle subdivisions of spherical unity inherently noninterchangeable with one another when turned inside out, whereas they are interchangeable with one another by insideouting when in their planar- faceted polyhedral state.
456.04 We thus find the split-phase positive-and-negativeness of oddnumber-of- vertexial-angle systems to be inherently askewed and insideoutingly dichotomized omnisymmetries. This surface phase of dichotomization results in superficial, disorderly interpatterning complementation. This superficially disarrayed complementation is disclosed when the 15 great circles produced by extension of all 30 edges of the icosahedron's 20 triangles are folded radially in conformity to the central interangling of the 120 triangles' spherical arc edges.
456.05 The 15 great circles of the icosahedron interact to produce 15 "chains" of three varieties of four corner-to-corner, sausage-linked, right triangles, with four triangles in each chain. These 15 chains of 60 great-circle triangles are each interconnectible corner- to-corner to produce a total spherical surface subdivided into 120 similar spherical triangles. An experiment with 15 unique coloring differentiations of the 15 chains of three sequential varieties of four triangles each, will exactly complete the finite sphere and the 15 great-circle integrities of total spherical surface patterning, while utterly frustrating any systematically orderly surface patterning. The 15 chains' 60 triangles' inadvertent formation of an additional 60 similar spherical triangles occurring between them, which exactly subdivides the entire spherical surface into 120 symmetrically interpatterned triangles__despite the local surface disorder of interlinkage of the three differently colored sets of four triangles composing the 15 chains__dramatically manifests the half-positive, half-negative, always and only coexisting, universal non-mirror-imaged complementarity inherently permeating all systems, dynamic or static, despite superficial disorder, whether or not visibly discernible initially.
456.10 Icosahedron as Contraction of Vector Equilibrium: The icosahedron represents the 12-way, omniradially symmetrical, transformative, rotational contraction of the vector equilibrium. This can be seen very appropriately when we join the 12 spheres tangent to one another around a central nuclear sphere in closest packing: this gives the correspondence to the vector equilibrium with six square faces and eight triangular faces, all with 60degree internal angles. If we llad rubber bands between the points of tangency of those 12 spheres and then removed the center sphere, we would find the 12 tangent spheres contracting immediately and symmetrically into the icosahedral conformation.
456.11 The icosahedron is the vector equilibrium contracted in radius so that the vector equilibrium's six square faces become 12 ridge-pole diamonds. The ridge-pole lengths are the same as those of the 12 radii and the 24 outside edges. With each of the former six square faces of the vector equilibrium now turned into two equiangle triangles for a total of 12, and with such new additional equiangled and equiedged triangles added to the vector equilibrium's original eight, we now have 20 triangles and no other surface facets than the 20 triangles. Whereas the vector equilibrium had 24 edges, we now have added six more to the total polyhedral system as it transforms from the vector equilibrium into the icosahedron; the six additional ridge poles of the diamonds make a total of 30 edges of the icosahedron. This addition of six vector edge lengths is equivalent to one great circle and also to one quantum. (See Sec. 423.10.)
456.12 We picture the location of the vector equilibrium's triangular faces in relation to the icosahedron's triangular faces. The vector equilibrium could contract rotatively, in either positive or negative manner, with the equator going either clockwise or counterclockwise. Each contraction provides a different superposition of the vector equilibrium's triangular faces on the icosahedron's triangular faces. But the centers of area of the triangular faces remain coincidental and congruent. They retain their common centers of area as they rotate.
456.13 We find that the 25 great circles of the icosahedron each pass through the 12 vertexes corresponding to the 25 great circles of the vector equilibrium, which also went through the 12 vertexes, as the number of vertexes after the rotational contraction remains the same.
456.20 Single-Layer Contraction: The icosahedron, in order to contract, must be a single-layer affair. You could not have two adjacent layers of vector equilibria and then have them collapse to become the icosahedron. But take any single layer of a vector equilibrium with nothing inside it to push it outward, and it will collapse into becoming the icosahedron. If there are two layers, one inside the other, they will not roll on each other when the radius contracts. The gears block each other. So you can only have this contraction in a single layer of the vector equilibrium, and it has to be an outside layer remote from other layers.
456.21 The icosahedron has only the outer shell layer, but it may have as high a frequency as nature may require. The nuclear center is vacant.
456.22 The single-shell behavior of the icosahedron and its volume ratio of 18.63 arouses suspicions about its relation to the electron. We appear to have the electron kind of shells operating in the nucleus-free icosahedron and are therefore not frustrated from contracting in that condition.
457.00 Great Circles of Icosahedron
457.01 Three Sets of Axes of Spin: The icosahedron has three unique symmetric sets of axes of spin. It provides 20 triangular faces, 12 vertexes, and 30 edges. These three symmetrically interpatterned topological aspects__ faces, vertexes, and mid-edges__ provide three sets of axes of symmetric spin to generate the spherical icosahedron projection's grid of 31 great circles.
457.02 The icosahedron has the highest number of identical and symmetric exterior triangular facets of all the symmetrical polyhedra defined by great circles.
457.10 When we interconnect the centers of area of the 20 triangular faces of the icosahedron with the centers of area of their diametrically opposite faces, we are provided with 10 axes of spin. We can spin the icosahedron on any one of these 10 axes toproduce 10 equators of spin. These axes generate the set of 10 great-circle equators of the icosahedron. We may also interconnect the midpoints of the 30 edges of the icosahedron in 15 sets of diametrically opposite pairs. These axes generate the 15 great-circle equators of the icosahedron. These two sets of 10 and 15 great circles correspond to the 25 great circles of the vector equilibrium.
457.20 Six Great Circles of Icosahedron: When we interconnect the 12 vertexes of the icosahedron in pairs of diametric opposites, we are provided with six axes of spin. These axes generate the six great-circle equators of the icosahedron. The six great circles of the icosahedron go from mid-edge to mid-edge of the icosahedron's triangular faces, and they do not go through any of its vertexes.
457.21 The icosahedron's set of six great circles is unique among all the seven axes of symmetry (see Sec. 1040), which include both the 25 great circles of the vector equilibrium and the 31 great circles of the icosahedron. It is the only set that goes through none of the 12 vertexes of either the vector equilibrium or the icosahedron. In assiduously and most geometrically avoiding even remote contact with any of the vertexes, they represent a new behavior of great circles.
457.22 The 12 vertexes in their "in-phase" state in the vector equilibria or in their "out-of-phase" state in the icosahedra constitute all the 12 points of possible tangency of any one sphere of a closest-packed aggregate with another sphere, and therefore these 12 points are the only ones by which energy might pass to cross over into the next spheres of closest packing, thus to travel their distance from here to there. The six great circles of the icosahedron are the only ones not to go through the potential intertangency points of the closest-packed unit radius spheres, ergo energy shunted on to the six icosahedron great circles becomes locked into local holding patterns, which is not dissimilar to the electron charge behaviors.

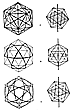Fig. 457.30A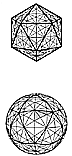

Fig. 457.30B 		457.30 Axes of Symmetry of Icosahedron: We have now described altogether the 10 great circles generated by the 10 axes of symmetry occurring between the centers of area of the triangular faces; plus 15 axes from the midpoints of the edges; plus six axes from the vertexes. 10 + 15 + 6 = 31. There is a total of 31 great circles of the icosahedron.

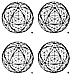Fig. 457.40 		457.40 Spherical Polyhedra in Icosahedral System: The 31 great circles of the spherical icosahedron provide spherical edges for three other polyhedra in addition to the icosahedron: the rhombic triacontrahedron, the octahedron, and the pentagonal dodecahedron. The edges of the spherical icosahedron are shown in heavy lines in the illustration.
457.41 The spherical rhombic triacontrahedron is composed of 30 spherical rhombic diamond faces.
457.42 The spherical octahedron is composed of eight spherical triangles.
457.43 The spherical pentagonal dodecahedron is composed of 12 spherical pentagons.
458.00 Icosahedron: Great Circle Railroad Tracks of Energy
458.01 Whereas each of the 25 great circles of the vector equilibrium and the icosahedron goes through the 12 vertexes at least twice; and whereas the 12 vertexes are the only points of intertangency of symmetric, unit-radius spheres, one with the other,in closest packing of spheres; and inasmuch as we find that energy charges always follow the convex surfaces of systems; and inasmuch as the great circles represent the most economical, the shortest distance between points on spheres; and inasmuch as we find that energy always takes the most economical route; therefore, it is perfectly clear that energy charges passing through an aggregate of closest-packed spheres, from one to another, could and would employ only the 25 great circles as the greatcircle railroad tracks between the points of tangency of the spheres, ergo, between points in Universe. We can say, then, that the 25 great circles of the vector equilibrium represent all the possible railroad tracks of shortest energy travel through closest-packed spheres or atoms.
458.02 When the nucleus of the vector equilibrium is collapsed, or contracted, permitting the 12 vertexes to take the icosahedral conformation, the 12 points of contact of the system go out of register so that the 12 vertexes that accommodate the 25 great circles of the icosahedron no longer constitute the shortest routes of travel of the energy.
458.03 The icosahedron could not occur with a nucleus. The icosahedron, in fact, can only occur as a single shell of 12 vertexes remote from the vector equilibrium's multi- unlimited-frequency, concentric-layer growth. Though it has the 25 great circles, the icosahedron no longer represents the travel of energy from any sphere to any tangent sphere, but it provides the most economical route between a chain of tangent icosahedra and a face-bonded icosahedral structuring of a "giant octahedron's" three great circles, as well as for energies locked up on its surface to continue to make orbits of their own in local travel around that single sphere's surface.
458.04 This unique behavior may relate to the fact that the volume of the icosahedron in respect to the vector equilibrium with the rational value of 20 is 18.51 and to the fact that the mass of the electron is approximately one over 18.51 in respect to the mass of the neutron. The icosahedron's shunting of energy into local spherical orbiting, disconnecting it from the closest-packed railroad tracks of energy travel from sphere to sphere, tends to identify the icosahedron very uniquely with the electron's unique behavior in respect to nuclei as operating in remote orbit shells.
458.05 The energy charge of the electron is easy to discharge from the surfaces of systems. Our 25 great circles could lock up a whole lot of energy to be discharged. The spark could jump over at this point. We recall the name electron coming from the Greeks rubbing of amber, which then discharged sparks. If we assume that the vertexes are points of discharge, then we see how the six great circles of the icosahedron__which never get near its own vertexes__may represent the way the residual charge will always remain bold on the surface of the-icosahedron.
458.06 Maybe the 31 great circles of the icosahedron lock up the energy charges of the electron, while the six great circles release the sparks.
458.10 Icosahedron as Local Shunting Circuit: The icosahedron makes it possible to have individuality in Universe. The vector equilibrium never pauses at equilibrium, but our consciousness is caught in the icosahedron when mind closes the switch.
458.11 The icosahedron's function in Universe may be to throw the switch of cosmic energy into a local shunting circuit. In the icosahedron energy gets itself locked up even more by the six great circles__which may explain why electrons are borrowable and independent of the proton-neutron group.

Fig. 458.12 		458.12 The vector-equilibrium railroad tracks are trans-Universe, but the icosahedron is a locally operative system.
459.00 Great Circle Foldabilities of Icosahedron

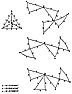Fig. 459.01 		459.01 The great circles of the icosahedron can be folded out of circular discs of paper by three different methods: (a) 15 multi-bow ties of four tetrahedra each; (b) six pentagonal bow ties; and (c) 10 multi-bow ties. Each method defines certain of the surface arcs and central angles of the icosahedron's great circle system, but all three methods taken together do not define all of the surface arcs and central angles of the icosahedron's three sets of axis of spin.
459.02 The 15 great circles of the icosahedron can be folded into multibow ties of four tetrahedra each. Four times 15 equals 60, which is half the number of triangles on the sphere. Sixty additional triangles inadvertently appear, revealing the 120 identical spherical triangles which are the maximum number of like units which may be used to subdivide the sphere.
459.03 The six great circles of the icosahedron can be folded from central angles of 36 degrees each to form six pentagonal bow ties. (See illustration 458.12.)
Next Section: 460.00
Copyright © 1997 Estate of R. Buckminster Fuller