519.00 Point

519.01 What we really mean by a point is an unresolved definition of an activity. A point by itself does not enclose. There are no indivisible points.

519.02 Without insideness, there is no outsideness; and without either insideness or outsideness, there is only a locus fix. Ergo, "points" are inherently nondemonstrable, and the phenomena accommodated by the packaged word point will always prove to be a focal center of differentiating events. A locus fix constitutes conceptual genesis that may be realized in time. Any conceptual event in Universe must have insideness and outsideness. This is a fundamentally self-organizing principle.

519.03 Points are complex but only as yet nondifferentiably resolvable by superficial inspection. A star is something you cannot resolve. We call it a point, playing Euler's game of crossings. One locus fix does not have an insideness and an outsideness. It takes four to define insideness and outsideness. It is called a point only because you cannot resolve it. Two remotely crossing trajectories have no insideness or outsideness, but do produce optically observable crossings, or locus fixes, that are positionally alterable in respect to a plurality of observation points. A point's definitively unresolved event relationships inherently embrace potential definitions of a complex of local events. When concentrically and convergently resolved, the "point" proves to be the "center" __the zero moment of transition from going inwardly and going outwardly.

519.10 Physical points are energy-event aggregations. When they converge beyond the critical fall-in proximity threshold, they orbit coordinatedly, as a Universe-precessed aggregate, as loose pebbles on our Earth orbit the Sun in unison, and as chips ride around on men's shoulders. A "point" often means "locus of inflection" when we go beyond the threshold of critical proximity and the inness proclivity prevails, in contradistinction to the differentiable other fallen-in aggregates orbiting precessionally in only mass-attractively cohered remoteness outwardly beyond the critical-proximity threshold.

519.20 If light or any other experiential phenomenon were instantaneous, it would be less than a point.

519.21 A point on a sphere is never an infinitesimal tangency with a plane.

519.22 The domains of vertexes are spheres.

519.30 For every event-fixed locus in Universe, there are six uniquely and exclusively operative vectors. (See Sec. 537, Twelve Universal Degrees of Freedom.)

520.00 Wavilinearity: Fixes

520.01 Linear does not mean straight. Lines are energy-event traceries, mappings, trajectories. Physics has found no straight lines: only waves consisting of frequencies of directional inflections in respect to duration of experience.

520.02 Calculus treats discretely and predictively with frequency change rates and discrete directions of angles of change of the omnicurvilinear event quanta's successively occurring positionings: fixes.

520.03 Fixes consist of both angular and frequency (size) observations. Coincidental angle and dimension observations provide fixes.

520.10 Spiralinearity

520.101 Regenerative precession imposes wavilinearity on vectors and tensors. Wavilinearity is spiralinear.

520.11 All actions are spiral because they cannot go through themselves and because there is time. The remote aspect of a spiral is a wave because there are no planes.

520.12 As with coil springs, in tensors and vectors of equal magnitude, the spiralinearity of the vector is shorter in overall spatial extent than is the spiralinearity of the tensor. Compressed lines or rods tend to arcs of diminishing radius; tensed lines or rods tend to arcs of increasing radius.

521.00 Vectors: Trajectories

521.01 A vector manifests a unique energy event__either potential or realized__expressed discretely in terms of direction, mass, velocity, and distance. A vector is a partial generalization, being either metaphysically theoretical or physically realized, and in either sense an abstraction of a special case, as are numbers both abstract (empty sets) or special-case (filled sets).

521.02 A vector always has unique direction relative to other events. It is discrete because it has a beginning and an end. Its length represents energy magnitude, the produce of its velocity and its mass. The direction is angular in respect to the axis of reference of the observer or in respect to an omnidirectional coordinate system.

521.03 Vectors are wavilinear lines of very high frequency regeneration of events whose high frequencies and whose short wavelengths only superficially appear to be "straight." Since neither light nor any other experiential phenomena are instantaneous. They are "linear." If they were instantaneous, they would be less than a point. The terminal of an action's vector occurs "later. "

521.04 Vectors are spearlike lines representing the integrated velocities, directions, and masses of the total aggregate of nonredundant forces operating complexedly within a given energy event as it transpires within a generalized environment of other experiences whose angular orientations and interdistance relationships are known.

521.05 Vectors always and only coexist with two other vectors, whether or not expressed; i.e., every event has its nonsimultaneous action, reaction, and resultant. (See Sec. 511, Energy Event.) But every event has a cosmic complementary; ergo, every vector's action, reaction, and resultant have their cosmic tripartite complementaries.

521.06 A vector has two vertexes with angles around each of its vertexial ends equal to 0 degrees. Every vector is reversible, having its negative alternate. For every point in Universe, there are six uniquely and exclusively operative vectors. (See Sec. 537, Twelve Universal Degrees of Freedom.)

521.07 Every event is six-vectored. There are six vectors or none.

521.08 Vectors are size. The size of a vector is its overall wavilinear length.

521.09 A vector is one-twelfth of relevant system potential.

521.10 Tensors

521.101 Vectors and tensors constitute all elementary dimension. A vector represents an expelling force and a tensor an impelling force.

521.20 Lines

521.201 Pure mathematics' axiomatic concepts of straight lines are completely invalid. Lines are vector trajectories.

521.21 The word line was nondefinable: infinite. It is the axis of intertangency of unity as plural and minimum two. Awareness begins with two. This is where epistemology comes in. The "line" becomes the axis of spin. Even two balls can exhibit both axial and circumferential degrees of freedom. (See Sec. 517.01, Sec. 537.22, and Sec. 240, Synergetics Corollaries, Subsec. 06, 13, 14, 15, 20, 21, 22, 24, 25, 26, 27, 29, 30, 31, 35, 36.)

521.22 A line is a directional experience. A line is specific like in, while out is anydirectional. Lines are always curvilinearly realized because of universal resonance, spinning, and orbiting.

521.23 A point is not a relationship. A line is the simplest relationship. Lines are relativity. A line is the first order of relativity: the basic sixness of minimum system and the cosmically constant sixness of relationship identifies lines as the relativity in the formula N2 - N ---------------- . 2

521.30 Omnidirectional Force Vectors

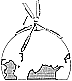Fig. 521.30

521.30 Galileo's parallelogram of forces is inadequate to account for resultants other than in the special-case, one-plane, billiard-table situation. Force vectors must express the omnidirectional interaction of forces, with lengths proportional to their mass times the velocity, and indicating that there are unique directions in Universe.

521.31 When we vector the course of one ship on a collision course with a second ship, the resultant of forces in Galileo's diagram would have them waltzing off together some 12 miles to the north-northeast. But all sane men can see such behavior is just what ships do not display after a collision. One of the two ships colliding on the wavy surface of spherical Earth may go a few hundred feet in the direction of Galileo's resultant of forces, but not 12 miles. But the other one probably goes in toward the center of Earth__which isn't in the diagram at all.

521.32 When ships run into each other, they actually first rise outwardly from Earth's center because in acceleration both were trying to leave Earth. (If they could accelerate faster, like rockets, they would leave Earth.) In reality, there are four forces operating. Two rise outwardly against gravity, accelerating conically together before they subside, when one or both go to the bottom. In addition to the vector for each ship, there is gravity plus the resultant. We are operating omnidimensionally, and this is what the minimum set of forces is. The pattern of force lines looks very much like a music stand: three vectorial legs spread out with a fourth vertical vector. (See Secs. 621.20 and 1012.37.)

522.00 Deliberately Nonstraight Line

522.01 The so-called pure mathematician's straight line must be the "impossible"; it must be instantly infinite in two infinitely remote opposite directions. All of its parts must be absolutely, uniformly nothing and simultaneously manifest as discretely, and infinitely divisible, increments. It may not be generated progressively or drawn physically, in time, as an experimentally produced action trajectory of one system modifying another. Microscopic inspection of the impressed, graven, deposited, or left-behind trails of all physical Universe's action trajectories always discloses a complex of gross, noninfinite, nonstraight, non-equal-magnitude irregularities. Progressively closer inspections of experimentally attempted demonstrations by pure mathematicians of their allegedly "straight" lines disclose increasingly volumetric aberration and angular digressions from straightness.

522.02 "Straight lines" may be axiomatically invoked but are nonrealizable in pure imagination: image-ination involves reconsidered and hypothetically rearranging the "furniture" of remembered experience as retrieved from the brain bank. Straight lines are axiomatically self-contradictory and selfcanceling hypothetical ventures. Physics has found only waves, no straight lines. Physics finds the whole physical Universe to be uniquely differentiated and locally defined as "waves."

522.03 The deliberately nonstraight line of synergetics employs the mathematicians' own invention for dealing with great dilemmas: the strategy of reductio ad absurdum. Having moments of great frustration, the mathematician learned to forsake looking for local logic; he learned to go in the opposite direction and deliberately to choose the most absurd. And then, by progressively eliminating the degrees of absurdity, he could work back to the not too absurd. In hunting terms, we call this quarrying his objective. Thus he is able at least to learn where his quarry is within a small area.

522.04 To develop methodically a very much less crooked line than that of conventional geometry, we start to produce our deliberately nonstraight line by taking a simple piece of obviously twisted rope. We will use Dacron, which is nonstretchable (nylon will stretch, and manila is very offensively stretchable). We then take the two ends of our rope and splice them into each other to form a loop. This immediately contradicts the definition of a straight line, which is that it never returns upon itself. We can take the two parts of the rope loop that are approximately parallel to one another and hold these two parts in our hands. We may call this pairing. Holding one hand on one of the pairs, we can slide the rope on the other hand, continually pairing it away from the point of first pairing. As we massage the two parts along, our hand finally gets to where the rope comes into a very sharp little loop and turns to come back on itself. We can hold it very tight at this point and put a little ribbon on the bend, the arch where it bends itself back. Sliding our hands the other way, holding and sliding, holding and sliding, massaging the rope together, we come to the other looping point and carefully put a ribbon marker in the bend of the arch. Having carefully made a rope that returns upon itself, we have now divided unity into two approximately equal halves.

522.05 Heisenberg makes it experientially clear that we cannot be absolutely exact. The act of measuring alters that which is measured. But with care we can be confident that we have two experiencially satisfactory halves of the total rope circuit existing between our two ribbon markers. Proceeding further, we can bring the ribbon-marked, half-points together, thus to divide the rope into four equal parts of unity. We can separately halve each of those quarter-lengths of the rope's closed-circuit unity to produce one-eighth unity length, while avoiding compounding of error. Each time we halve a local fraction, we halve any residual error. We can evenly subdivide our deliberately nonstraight line into as many small fractions as may be desirable.

522.06 We now ask four friends each to take hold of a half- or a quarter-point in the rope, and then ask them to walk away from each other until the rope unity is taut. We ask them to lower their four-sided geometrical figure to the floor and ask another friend to drive nails into the floor inside the four tightly stretched corners of the rope. A diamond rope pattern is thus produced with its corners marked A, B, C, and D. We are provided with plenty of proofs about equilateral parallelograms; we know that if the sides are equal in length, we can assume them to be approximately parallel because the wall we have nailed them to is an approximate plane. It may be pretty rough as the mathematicians talk about planes, but it is nonetheless a satisfactory plane for our purposes.

522.07 We next put in more nails in the floor at the ribbon-marked eighth points. C is the right-hand corner of the diamond, and D is the top of the diamond. We can call the bottom half of the diamond a V, and we can call the top half of the diamond a lambda. Putting nails at the one-eighth points means that halfway down from A to B there is a nail and halfway from B upward to C there is a nail. Halfway from C upward to D we put a nail at the eighth point. Then halfway down from D back to A again we put another nail at the eighth point. We then take the rope off D and place it over those one-eighth nails. The rope now changes from a lambda pattern into an "M" form. Because it is an equilateral parallelogram, we know that the new middle loop must be at the center of the diamond. We place a nail at this center of the diamond and mark it O. We next go from C, which is at the extreme right-hand corner of the diamond, down to take the rope off B. Taking the rope off the V (which used to be ABC), we convert the V to a W__with the bottom points of the W at the one-eighth-point nails. We then move the rope off B and up to the center of the diamond also. This gives us two diamonds, two little diamonds strung end-to-end together at the center of the big diamond. Their extreme ends are at A and C. Because we know that these are all equilateral parallelograms, we know that the length of the new letter M is the same as the length of the new letter W. We can now give these new one- eighth points the designations E, F, G, and H. So it now reads AHOGC and AEOFC. And we have two beautiful diamonds.

522.08 From now on, all we have to do is convert each of these diamonds in the same manner into two smaller ones. We convert the two diamonds into four. And then the four into eight. And the eight into 16. But the chain of diamonds always remains A__C in overall length. Both the altitudes and lengths of the diamonds are continually halving; thus what we are doing is simply increasing the frequency of the modular subdivision of the original unity of the rope. As the frequency of the wavelike subdivisions is multiplied, the deliberately nonstraight line approaches contractively toward straight behaviors. The rope remains exactly the same length, but its two parts are getting closer and closer to one another. The plane of the floor is really an illusion. As we get to a very high frequency of diamonds, we realize that instead of doing it the way we did, we could simply have twisted the original rope so that it would be a series of spirals of the same number as that of the chain of diamonds. We look at the profile of the rope and realize that all we are seeing is twice as many twists every time__at every progression. This gives us a very intimate concept of what actually happens in wave phenomena.

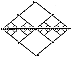Fig. 522.09

522.09 The old-fashioned physicist used to put one nail in the wall, fasten a rope to it, and stand back and throw a whip into the rope. The whip goes to the nail on the wall and then comes back to his hand and stops. That is the prime characteristic of waves. They always make a complete cycle. That is why, for instance, gears are always whole circles. A gear is a fundamental wave phenomenon. Electromagnetic waves always close back upon themselves. Deliberately nonstraight lines are round-trip circuits.

522.10 Our deliberately nonstraight-line model provides us whatever frequency of modular subdivision we want in unity, which is the cycle. This is what we mean by frequency of modular subdivision, whether unity is a sphere or a circle. What is going on in our rope, the way we have handled it, we make it into unity as a cycle. We see these waves going in a round-trip trajectory pattern from A to the extreme point C and back again to A. The overall distance traveled by any of the routes remains the same. So what we see on the floor or in the diamond chain diagram is a true model of basic wave phenomena. As we double the frequency and halve the wavelength of positive and negative waves, we swiftly arrive at a visibly far less crooked condition and approach relative straightness. We can see quite clearly that we do not have to increase the subdividing of those diamonds many times before they tend to look like a straight line as far as your eye and my eye can see. This concept agrees elegantly with fundamental wave theory as predicated on electromagnetic experimentation.

522.11 For instance, on an engineer's scale you and I can see 50 divisions of an inch. We can see l/50th of an inch, but 1/100th of an inch goes gray and blurred. When we get to where an inch of the deliberately nonstraight line has more than 100 subdivisions, it looks like an absolutely straight line. When we get into the kinds of frequencies that characterize light waves, we get into very, very high numbers, and we can understand that what we call a line of sight has become so thin that it is invisible altogether. So we can understand that when the mathematician asked for a line of sight, which felt so good to him, he was asking for something that is really very beautifully imaginary. It was always a deliberately nonstraight line.

522.20 All experiments show that with ever closer inspections, the mathematicians' "straight" lines become obviously ever less straight. On the other hand, the quasi-straight line, which is demonstrated here as the deliberately nonstraight line, does get progressively straighter. Tending toward a greater straightness than that which is physically demonstrable, the deliberately nonstraight line thus serves all the finite geometries heretofore employed schematically by the mathematicians' alleged but unprovable straight lines, i.e., to demonstrate proof of the Euclidian and non-Euclidian geometrical propositions.

522.21 "Lines of sight" taken with transits are truer than string lines or penciled lines. Sight approaches "straight" behaviors. Lines of sight are high-frequency energy- wave interactions. Because the truest lines of sight are energy-wave quanta, they are always finite. The mathematician might say, "Oh, I mean a much straighter line than you can draw, I mean as straight and intangible as a line of sight." Then you remind the mathematician that when you have your transit's telescope focused on the "kissing point," as Earth's horizon becomes tangent to Sun's disc at daylight's end, you must remember that it takes eight minutes for the light to reach us from the Sun. Wherefore, the Sun has not been there for eight minutes, and you must admit that you are "seeing" the Sun around and beyond the horizon, which proves that your "line of sight" is curved, not straight. Due to the lag in the speed of light, Sun has not been there in a direct line of sight for eight minutes, so you are looking around the horizon through a curved "pipe" of light. This is what Einstein referred to as curved space.

522.22 To provide a more accurate identity of the only apparently straight-line phenomenon that the pure mathematician had erroneously thought of as "the shortest distance between two points," Einstein reinvoked the elliptical geometry of the mathematician Riemann and instituted the present concept of geodesic lines, which we may describe experimentally as "the most economic relationships between two event foci."

522.23 To comprehend and apprehend experimentally such "most economic relationships," all that you need do is to attempt to hit a flying object with a bullet fired by you from a gun. If you fire at the flying object where it is at the moment you fire, you will not hit it. You must fire at where you figure it is going to be at a later moment when it would most probably collide with your bullet. Gravity will start curving your bullet toward Earth as soon as it leaves your gun. The amount of curvature may be imperceptible to you, but it is easily detected by using a camera and a tracer firing charge. The air is always in motion, and your bullet will corkscrew ever so mildly between you and the flying object. This corkscrewing of the geodesic line, which is the most economical time-distance-effort relationship between the gun, the firer, and the flying object he hits, is dramatically shown in night photography of dogfights of World-War-II airplanes firing machine-gun tracer bullets at one another, with one being hit while the photographs are taken by a third plane flying in close vicinity of the dogfight.

522.30 Reduction by Bits

522.301 What the mathematicians thought was a straight line is not a straight line; it is an ultravisible, high-frequency, linearly articulated, spiral-wave event. The binary- mathematics methodology of progressive halving, or cybernetic "bitting," not only explains linear-wave phenomena but also identifies Pythagoras's halving of the string of a musical instrument to gain an exact musical octave__or his "thirding" of the musical string to produce the musical fifths of progression of flat and sharp keys.

522.31 The computer programmed to employ the cybernetic bits of binary mathematics progressively subdivides until one of its peak or valley parts gets into congruence with the size and position of the unit we seek. The identification process is accounted for in the terms of how many bits it takes to locate the answer, i.e., to "tune in."

522.32 Starting with whole Universe, we quickly reach any local system within the totality by differentiating it out temporarily from the whole for intimate consideration. We do so by the process of reduction by bits.

522.33 All irrelevancies fall into two main categories, or bits. Bits break up finite wholes into finite parts.

522.34 Once you state what your realistic optimum recognition of totality consists of, then you find how many bits or subdivision stages it will take to isolate any items within that totality. It is like the childhood game of Twenty Questions: You start by saying, "Is it physical or metaphysical?" Next: "Is it animate or inanimate?" (One bit.) "Is it big or little?" (Two bits.) "Is it hot or cold?" (Three bits.) It takes only a few bits to find out what you want. When we use bit subdivision to ferret out the components of our problems, we do exactly what the computer is designed to do. The computer's mechanism consists of simple go-no go, of yes and no circuit valves, or binary mathematics valves. We keep "halving" the halves of Universe until we refine out the desired bit. In four halvings, you have eliminated 94 percent of irrelevant Universe. In seven halvings, you have removed 99.2 percent of irrelevant Universe. Operating as fast as multithousands of halvings per second, the computer seems to produce instantaneous answers.

522.35 Thus we learn that our naturally spontaneous faculties for acquiring comprehensive education make it easy to instruct the computer and thus to obtain its swift answers. Best of all, when we get the answers, we have comprehensive awareness of the relative significance, utility, and beauty of the answers in respect to our general universal evolution conceptioning.

522.36 Our method of demonstrating the nature of the special-case experiences out of which the pure mathematicians' imaginary generalized case of his pure straight line was evolved, also contains within it the complete gears-interlocking of quantum-wave mechanics and vectorial geometry, which are coordinately contained in synergetics with computer binary "bitting."

523.00 Vertexes: Crossings

523.01 Euler showed that where we have two lines__any kind of lines, crooked or not so crooked__where the lines cross is distinctly different from where the lines do not cross. The pattern of two or more lines crossing one another is also completely distinguishable from any single line by itself. We call this crossing or convergence of lines a vertex. This is absolute pattern uniqueness.

523.02 Crossings are superimposed lines. They do not go through each other. They are just a fix__what physicists call points.

523.03 In a structural system, the number of vertexes is always divisible by four and the number of triangle edges is always divisible by six. Edges and vertexes do not come out as the same number systems, but you can describe the world both ways and not be redundant.