 Tetrahedron
Tetrahedron

|
620.01
 In the conceptual process of developing the disciplines
for carrying on the
process of consideration, the process of temporarily
putting aside the irrelevancies and
working more closely for the relationships between the
components that are considered
relevant, we find that a geometry of configuration emerges
from our awareness of the
minimum considered components. A minimum constellation
emerges from our
preoccupation with getting rid of the irrelevancies.
The geometry appears out of pure
conceptuality. We dismiss the irrelevancies in the search
for understanding, and we finally
come down to the minimum set that may form a system
to divide Universe into
macrocosm and microcosm, which is a set of four items
of consideration. The minimum
consideration is a four-star affair that is tetrahedral.
Between the four stars that form the
vertexes of the tetrahedron, which is the simplest system
in Universe, there are six edges
that constitute all the possible relationships between
those four stars.
In the conceptual process of developing the disciplines
for carrying on the
process of consideration, the process of temporarily
putting aside the irrelevancies and
working more closely for the relationships between the
components that are considered
relevant, we find that a geometry of configuration emerges
from our awareness of the
minimum considered components. A minimum constellation
emerges from our
preoccupation with getting rid of the irrelevancies.
The geometry appears out of pure
conceptuality. We dismiss the irrelevancies in the search
for understanding, and we finally
come down to the minimum set that may form a system
to divide Universe into
macrocosm and microcosm, which is a set of four items
of consideration. The minimum
consideration is a four-star affair that is tetrahedral.
Between the four stars that form the
vertexes of the tetrahedron, which is the simplest system
in Universe, there are six edges
that constitute all the possible relationships between
those four stars.
|

|
620.02
 The tetrahedron occurs conceptually independent of
events and independent
of relative size.
The tetrahedron occurs conceptually independent of
events and independent
of relative size.
|

|
620.03
 By tetrahedron, we mean the minimum thinkable set
that would subdivide
Universe and have interconnectedness where it comes
back upon itself. The four points
have six interrelatednesses. There are two kinds of
number systems involved: four being
prime number two and six being prime number three. So
there are two very important
kinds of oscillating quantities numberwise, and they
begin to generate all kinds of
fundamentally useful mathematics. The basic structural
unit of physical Universe
quantation, tetrahedron has the fundamental prime number
oneness.
By tetrahedron, we mean the minimum thinkable set
that would subdivide
Universe and have interconnectedness where it comes
back upon itself. The four points
have six interrelatednesses. There are two kinds of
number systems involved: four being
prime number two and six being prime number three. So
there are two very important
kinds of oscillating quantities numberwise, and they
begin to generate all kinds of
fundamentally useful mathematics. The basic structural
unit of physical Universe
quantation, tetrahedron has the fundamental prime number
oneness.
|

|
620.04
 Around any one vertex of the tetrahedron, there are
three planes. Looking
down on a tetrahedron from above, we see three faces
and three edges. There are these
three edges and three faces around any one vertex. That
seems very symmetrical and nice.
You say that is logical; how could it be anything else?
But if we think about it some more,
it may seem rather strange because we observe three
faces and three edges from an
inventory of four faces and six edges. They are not
the same inventories. It is interesting
that we come out with symmetry around each of the points
out of a dissimilar inventory.
Around any one vertex of the tetrahedron, there are
three planes. Looking
down on a tetrahedron from above, we see three faces
and three edges. There are these
three edges and three faces around any one vertex. That
seems very symmetrical and nice.
You say that is logical; how could it be anything else?
But if we think about it some more,
it may seem rather strange because we observe three
faces and three edges from an
inventory of four faces and six edges. They are not
the same inventories. It is interesting
that we come out with symmetry around each of the points
out of a dissimilar inventory.
|

|
620.05
 The tetrahedron is the first and simplest subdivision
of Universe because it
could not have an insideness and an outsideness unless
it had four vertexes and six edges.
There are four areal subdivisions and four interweaving
vertexes or prime convergences in
its six-trajectory isolation system. The vertexial set
of four local-event foci coincides with
the requirement of quantum mathematics for four unique
quanta numbers for each
uniquely considerable quantum.
The tetrahedron is the first and simplest subdivision
of Universe because it
could not have an insideness and an outsideness unless
it had four vertexes and six edges.
There are four areal subdivisions and four interweaving
vertexes or prime convergences in
its six-trajectory isolation system. The vertexial set
of four local-event foci coincides with
the requirement of quantum mathematics for four unique
quanta numbers for each
uniquely considerable quantum.
|
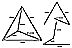 Fig. 620.06 |
620.06
 With three positive edges and three negative edges,
the tetrahedron provides
a vectorial quantum model in conceptual array in which
the right helix corresponds to the
proton set (with electron and antineutrino) and the
left helix corresponds to the neutron
set (with positron and neutrino). The neutron group
has a fundamental leftness and the
proton group has a fundamental rightness. They are not
mirror images. In the tetrahedron,
the two groups interact integrally. The tetrahedron
is a form of energy package.
With three positive edges and three negative edges,
the tetrahedron provides
a vectorial quantum model in conceptual array in which
the right helix corresponds to the
proton set (with electron and antineutrino) and the
left helix corresponds to the neutron
set (with positron and neutrino). The neutron group
has a fundamental leftness and the
proton group has a fundamental rightness. They are not
mirror images. In the tetrahedron,
the two groups interact integrally. The tetrahedron
is a form of energy package.
|

|
620.07
 The tetrahedron is transformable, but its topological
and quantum identity
persists in whole units throughout all experiments with
physical Universe. All of the
definable structuring of Universe is tetrahedrally coordinate
in rational number increments
of the tetrahedron.
The tetrahedron is transformable, but its topological
and quantum identity
persists in whole units throughout all experiments with
physical Universe. All of the
definable structuring of Universe is tetrahedrally coordinate
in rational number increments
of the tetrahedron.
|

|
620.08
 Organic chemistry and inorganic chemistry are both
tetrahedrally coordinate.
This relates to the thinking process where the fundamental
configuration came out a
tetrahedron. Nature's formulations here are a very,
very high frequency. Nature makes
viruses in split seconds. Whatever she does has very
high frequency. We come to
tetrahedron as the first spontaneous aggregate of the
experiences. We discover that nature
is using tetrahedron in her fundamental formulation
of the organic and inorganic
chemistry. All structures are tetrahedrally based, and
we find our thoughts resolving
themselves spontaneously into the tetrahedron as it
comes to the generalization of the
special cases that are the physics or the chemistry.
Organic chemistry and inorganic chemistry are both
tetrahedrally coordinate.
This relates to the thinking process where the fundamental
configuration came out a
tetrahedron. Nature's formulations here are a very,
very high frequency. Nature makes
viruses in split seconds. Whatever she does has very
high frequency. We come to
tetrahedron as the first spontaneous aggregate of the
experiences. We discover that nature
is using tetrahedron in her fundamental formulation
of the organic and inorganic
chemistry. All structures are tetrahedrally based, and
we find our thoughts resolving
themselves spontaneously into the tetrahedron as it
comes to the generalization of the
special cases that are the physics or the chemistry.
|

|
620.09
 We are at all times seeking how it can be that nature
can develop viruses or
billions of beautiful bubbles in the wake of a ship.
How does she formulate these lovely
geometries so rapidly? She must have some fundamentally
pure and simple way of
developing these extraordinary life cells at the rate
she develops them. When we get to
something as simple as finding that the tetrahedron
is the minimum thinkable set that
subdivides Universe and has relatedness, and that the
chemist found all the structuring of
nature to be tetrahedral, in some cases vertex to vertex,
in others interlinked edge to edge,
we find, as our thoughts go this way, that it is a very
satisfying experience.
We are at all times seeking how it can be that nature
can develop viruses or
billions of beautiful bubbles in the wake of a ship.
How does she formulate these lovely
geometries so rapidly? She must have some fundamentally
pure and simple way of
developing these extraordinary life cells at the rate
she develops them. When we get to
something as simple as finding that the tetrahedron
is the minimum thinkable set that
subdivides Universe and has relatedness, and that the
chemist found all the structuring of
nature to be tetrahedral, in some cases vertex to vertex,
in others interlinked edge to edge,
we find, as our thoughts go this way, that it is a very
satisfying experience.
|

|
620.10
 All polyhedra may be subdivided into component tetrahedra,
but no
tetrahedron may be subdivided into component polyhedra
of less than the tetrahedron's
four faces.
All polyhedra may be subdivided into component tetrahedra,
but no
tetrahedron may be subdivided into component polyhedra
of less than the tetrahedron's
four faces.
|

|
620.11
 The triangle is the minimum polygon and the tetrahedron
is the minimum
structural system, for we cannot find an enclosure of
less than four sides, that is to say, of
less than 720 degrees of interior- (or exterior-) angle
interaction. The tetrahedron is a
tetrahedron independent of its edge lengths or its relative
volume. In tetrahedra of any
size, the angles are always sumtotally 720 degrees.
The triangle is the minimum polygon and the tetrahedron
is the minimum
structural system, for we cannot find an enclosure of
less than four sides, that is to say, of
less than 720 degrees of interior- (or exterior-) angle
interaction. The tetrahedron is a
tetrahedron independent of its edge lengths or its relative
volume. In tetrahedra of any
size, the angles are always sumtotally 720 degrees.
|

|
620.12
 Substituting the word tetrahedron for the number two
completes my long
attempt to convert all the previously unidentifiable
integers of topology into geometrical
conceptuality. Thus we see both the rational energy
quantum of physics and the
topological tetrahedron of the isotropic vector matrix
rationally accounting all physical
and metaphysical systems. (See Secs.
221.01
and
424.02.)
Substituting the word tetrahedron for the number two
completes my long
attempt to convert all the previously unidentifiable
integers of topology into geometrical
conceptuality. Thus we see both the rational energy
quantum of physics and the
topological tetrahedron of the isotropic vector matrix
rationally accounting all physical
and metaphysical systems. (See Secs.
221.01
and
424.02.)
|

|
621.00
 Constant Properties of the Tetrahedron
Constant Properties of the Tetrahedron
|
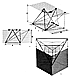 Fig. 621.01 |
621.01
 Evaluated in conventional terms of cubical unity,
the volume of a
tetrahedron is one-third the base area times the altitude;
in synergetics, however, the
volume of the tetrahedron is unity and the cube is threefold
unity. Any asymmetric
tetrahedron will have a volume equal to any other tetrahedron
so long as they have
common base areas and common altitudes. (See Sec.
923.20.)
Evaluated in conventional terms of cubical unity,
the volume of a
tetrahedron is one-third the base area times the altitude;
in synergetics, however, the
volume of the tetrahedron is unity and the cube is threefold
unity. Any asymmetric
tetrahedron will have a volume equal to any other tetrahedron
so long as they have
common base areas and common altitudes. (See Sec.
923.20.)
|

|
621.02
 Among geometrical systems, a tetrahedron encloses
the minimum volume
with the most surface, and a sphere encloses the most
volume with the least surface.
Among geometrical systems, a tetrahedron encloses
the minimum volume
with the most surface, and a sphere encloses the most
volume with the least surface.
|

|
621.03
 A cone is simply a tetrahedron being rotated. Omnidirectional
growth__which means all life__can be accommodated only
by tetrahedron.
A cone is simply a tetrahedron being rotated. Omnidirectional
growth__which means all life__can be accommodated only
by tetrahedron.
|

|
621.04
 There is a minimum of four unique planes nonparallel
to one another. The
four planes of the tetrahedron can never be parallel
to one another. So there are four
unique perpendiculars to the tetrahedron's four unique
faces, and they make up a four-
dimensional system.
There is a minimum of four unique planes nonparallel
to one another. The
four planes of the tetrahedron can never be parallel
to one another. So there are four
unique perpendiculars to the tetrahedron's four unique
faces, and they make up a four-
dimensional system.
|

|
621.05
 Sixth-powering is all the perpendiculars to the 12
faces of the rhombic
dodecahedron.
Sixth-powering is all the perpendiculars to the 12
faces of the rhombic
dodecahedron.
|

|
621.06
 When we try to fill all space with regular tetrahedra,
we are frustrated
because the tetrahedra will not fill in the voids above
the triangular-based grid pattern. But
the regular tetrahedron is a complementary space filler
with the octahedron. Sec.
951
describes irregular tetrahedral allspace fillers.
When we try to fill all space with regular tetrahedra,
we are frustrated
because the tetrahedra will not fill in the voids above
the triangular-based grid pattern. But
the regular tetrahedron is a complementary space filler
with the octahedron. Sec.
951
describes irregular tetrahedral allspace fillers.
|

|
621.07
 The tetrahedron and octahedron can be produced by
multilayered closest
packing of spheres. The surface shell of the icosahedron
can be made of any one layer-but
only one layer-of closest-packed spheres; the icosahedron
refuses radial closest packing.
The tetrahedron and octahedron can be produced by
multilayered closest
packing of spheres. The surface shell of the icosahedron
can be made of any one layer-but
only one layer-of closest-packed spheres; the icosahedron
refuses radial closest packing.
|
 Fig. 621.10 |
621.10
 Six Vectors Provide Minimum Stability: If we have
one stick standing
alone on a table, it may be balanced to stand alone,
but it is free to fall in any direction.
The same is true of two or three such sticks. Even if
the two or three sticks are connected
at the top in an interference, they are only immobilized
for the moment, as their feet can
slide out from under them. Four or five sticks propped
up as triangles are free to collapse
as a hinge action. Six members are required to complete
multidimensional stability__our
friend tetrahedron and the six positive, six negative
degrees of freedom showing up again.
Six Vectors Provide Minimum Stability: If we have
one stick standing
alone on a table, it may be balanced to stand alone,
but it is free to fall in any direction.
The same is true of two or three such sticks. Even if
the two or three sticks are connected
at the top in an interference, they are only immobilized
for the moment, as their feet can
slide out from under them. Four or five sticks propped
up as triangles are free to collapse
as a hinge action. Six members are required to complete
multidimensional stability__our
friend tetrahedron and the six positive, six negative
degrees of freedom showing up again.
|

|
621.20
 Tepee-Tripod: The tepee-tripod affords the best picture
of what happens
locally to an assemblage of six vectors or less. The
three sides of a tepee-tripod are
composed first of three vertical triangles rising from
a fourth ground triangle and
subsequently rocking toward one another until their
respective apexes and edges are
congruent. The three triangles plus the one on the ground
constitute a minimum system,
for they have minimum "withinness." Any one edge of
our tepee acting alone, as a pole
with a universal joint base, would fall over into a
horizontal position. Two edges of the
tepee acting alone form a triangle with the ground and
act as a hinge, with no way to
oppose rotation toward horizontal position except when
prevented from falling by
interference with a third edge pole, falling toward
and into congruence with the other two
poles' common vertex. The three base feet of the three
poles of the tepee-tripod would
slide away outwardly from one another were it not for
the ground, whose structural
integrity coheres the three feet and produces three
invisible chords preventing the three
feet from spreading. This makes the six edges of the
tetrahedron. (See Secs.
521.32
and
1012.37.)
Tepee-Tripod: The tepee-tripod affords the best picture
of what happens
locally to an assemblage of six vectors or less. The
three sides of a tepee-tripod are
composed first of three vertical triangles rising from
a fourth ground triangle and
subsequently rocking toward one another until their
respective apexes and edges are
congruent. The three triangles plus the one on the ground
constitute a minimum system,
for they have minimum "withinness." Any one edge of
our tepee acting alone, as a pole
with a universal joint base, would fall over into a
horizontal position. Two edges of the
tepee acting alone form a triangle with the ground and
act as a hinge, with no way to
oppose rotation toward horizontal position except when
prevented from falling by
interference with a third edge pole, falling toward
and into congruence with the other two
poles' common vertex. The three base feet of the three
poles of the tepee-tripod would
slide away outwardly from one another were it not for
the ground, whose structural
integrity coheres the three feet and produces three
invisible chords preventing the three
feet from spreading. This makes the six edges of the
tetrahedron. (See Secs.
521.32
and
1012.37.)
|

|
621.30
 Camera Tripod
Camera Tripod
|

|
621.31
 A simple model of the effective conservation of regenerative
Universe is to
be had in a camera tripod which, when its legs are folded
and parallel, finds the centers of
gravity and mass of its three individual legs in close
proximity to one another. As the legs
are progressively hinged outward from one another, the
respective centers of mass and
gravity recede from one another. From Newton's second
law we know that as bodies
increase their distance apart at an arithmetical rate,
their interattractiveness decreases at a
rate of the second power of the distance change__i.e.,
at double the distance the
interattraction decreases to one-quarter intensity.
Since the legs are fastened to one
another at only one end (the top end), if the floor
is slippery, the three bottom ends tend to
slide apart at an accelerated rate.
A simple model of the effective conservation of regenerative
Universe is to
be had in a camera tripod which, when its legs are folded
and parallel, finds the centers of
gravity and mass of its three individual legs in close
proximity to one another. As the legs
are progressively hinged outward from one another, the
respective centers of mass and
gravity recede from one another. From Newton's second
law we know that as bodies
increase their distance apart at an arithmetical rate,
their interattractiveness decreases at a
rate of the second power of the distance change__i.e.,
at double the distance the
interattraction decreases to one-quarter intensity.
Since the legs are fastened to one
another at only one end (the top end), if the floor
is slippery, the three bottom ends tend to
slide apart at an accelerated rate.
|

|
621.32
 We may think of the individual legs of the tripod
as being energy vectors.
The "length" of a vector equals the mass times the velocity
of the force operative in given
directions. We now open the equilengthed tripod legs
until their bottom terminals are
equidistant from one another, that distance being the
same length as the uniform length of
any one of the legs. Next we take three steel rods,
each equal in length, mass, and
structural strength to any one of the tripod legs, which
renders them of equal force vector
value to that of the tripod set. Next we weld the three
rods together at three corner angles
to form a triangle, against whose corners we will set
the three bottom ends of the three
downwardly and outwardly thrusting legs of the tripod.
As gravity pulls the tripod
Earthward, the tendency of these legs to disassociate
further is powerfully arrested by the
tensile integrity of the rod triangle on the ground,
in which both ends of all three are joined
together.
We may think of the individual legs of the tripod
as being energy vectors.
The "length" of a vector equals the mass times the velocity
of the force operative in given
directions. We now open the equilengthed tripod legs
until their bottom terminals are
equidistant from one another, that distance being the
same length as the uniform length of
any one of the legs. Next we take three steel rods,
each equal in length, mass, and
structural strength to any one of the tripod legs, which
renders them of equal force vector
value to that of the tripod set. Next we weld the three
rods together at three corner angles
to form a triangle, against whose corners we will set
the three bottom ends of the three
downwardly and outwardly thrusting legs of the tripod.
As gravity pulls the tripod
Earthward, the tendency of these legs to disassociate
further is powerfully arrested by the
tensile integrity of the rod triangle on the ground,
in which both ends of all three are joined
together.
|

|
621.33
 Assuming the three disassociative vectorial forces
of the tripod legs to be
equal to the associative vectorial force of the three-welded-together
rods, we find the
three-jointed closed system to be more effective than
the one-jointed system. In this model
the associative group in the closed triangle represents
the gravity of Universe and the
disassociative group__the tripod legs__represents the
radiation of Universe. The whole
model is the tetrahedron: the simplest structural system.
Assuming the three disassociative vectorial forces
of the tripod legs to be
equal to the associative vectorial force of the three-welded-together
rods, we find the
three-jointed closed system to be more effective than
the one-jointed system. In this model
the associative group in the closed triangle represents
the gravity of Universe and the
disassociative group__the tripod legs__represents the
radiation of Universe. The whole
model is the tetrahedron: the simplest structural system.
|

|
621.34
 Think of the head of the camera tripod as an energy
nucleus. We find that
when nuclear energy becomes disassociated as radiation,
it does so in a focused and
limited direction unless it is intercepted and reflectively
focused in a concave mirror.
Radiation is inherently omnidirectional in its distribution
from the nucleus outward, but it
can be directionally focused. Gravity is totally embracing
and convergently contractive
toward all its system centers of Scenario Universe,
and it cannot be focused. Like the
circular waves made by an object dropped in the water,
both gravitational and radiational
growth-in-time patterns are concentrically arrayed;
gravity convergently and contractively
concentric, radiation divergently and expansively concentric.
Frequency of concentricity
occurrence is relative to the cyclic system considered.
Think of the head of the camera tripod as an energy
nucleus. We find that
when nuclear energy becomes disassociated as radiation,
it does so in a focused and
limited direction unless it is intercepted and reflectively
focused in a concave mirror.
Radiation is inherently omnidirectional in its distribution
from the nucleus outward, but it
can be directionally focused. Gravity is totally embracing
and convergently contractive
toward all its system centers of Scenario Universe,
and it cannot be focused. Like the
circular waves made by an object dropped in the water,
both gravitational and radiational
growth-in-time patterns are concentrically arrayed;
gravity convergently and contractively
concentric, radiation divergently and expansively concentric.
Frequency of concentricity
occurrence is relative to the cyclic system considered.
|
| Next Section: 622.00 |