600.00 Structure

600.01 Definition: Structure

600.02 A structure is a self-stabilizing energy-event complex.
600.03 A structure is a system of dynamically stabilized self-interfering and thus self- localizing and recentering, inherently regenerative constellar association of a minimum set of four energy events.
600.04 Stability means angular invariability. Inherent means behavior principles that man discovers to be reliably operative under given conditions always and anywhere in Universe. Regenerative means local energy-pattern conservation. Constellar means an aggregation of enduring, cosmically isolated, locally co-occurring events dynamically maintaining their interpositioning: e.g., macroconstellations such as the Big Dipper, Orion, and the Southern Cross and microconstellations such as matter in general, granite, cheese, flesh, water, and atomic nuclei.
601.00 Pattern Conservation
601.01 It is a tendency for patterns either to repeat themselves locally or for their parts to separate out to join singly or severally with other patterns to form new constellations. All the forces operative in Universe result in a complex progression of most comfortable__i.e., least effort, rearrangings in which the macro-medio-micro star events stand dynamically together here and there as locally regenerative patterns. Spontaneously regenerative local constellations are cosmic, since they appear to be interoriented with angular constancy.
601.02 Structures are constellar pattern conservations. These definitions hold true all the way from whole Universe to lesser and local pattern differentiations all the way into the atom and its nuclear subassemblies. Each of the families of chemical elements, as well as their most complex agglomerations as super-star Galaxies, are alike cosmic structures. It is clear from the results of modern scientific experiments that structures are not things. Structures are event constellations.
602.01 Structural systems are cosmically localized, closed, and finite. They embrace all geometric forms-symmetric and asymmetric, simple and complex.
602.02 Structural systems can have only one insideness and only one out-sideness.
602.03 Two or more structures may be concentric and/or triangularly__triple- bondedly__interconnected to operate as one structure. Single-bonded (universally jointed) or double-bonded (hinged) means that we have two flexibly interconnected structural systems.
603.01 All structuring can be topologically identified in terms of tetrahedra. (See Sec. 362.)
604.00 Structural System
604.01 In a structural system:
  1. the number of vertexes (crossings) is always evenly divisible by two;
  2. the number of faces (openings) is always evenly divisible by four; and
  3. the number of edges (trajectories) is always evenly divisible by six.
605.01 Inasmuch as there are always and everywhere 12 fundamental degrees of freedom (six positive and six negative), and since every energy event is characterized by a threefold vectoring__an action, a reaction, and a resultant__all structures, symmetrical or asymmetrical, regular or irregular, simple or compound, will consist of the twelvefoldedness or its various multiples.
606.01 "Mathematics is the science of structure and pattern in general."1 Structure is defined as a locally regenerative pattern integrity of Universe. We cannot have a total structure of Universe. Structure is inherently only local and inherently regenerative.

(Footnote 1: From the Massachusetts Institute of Technology's 1951 offical catalog of the self-definition by M.I.T. Mathematics Department.)
606.02 Structures most frequently consist of the physical interrelationships of nonsimultaneous events.
606.03 One of the deeply impressive things about structures is that they cohere at all-particularly when we begin to know something about the atoms and realize that the components of atoms are really very remote from one another, so that we simply have galaxies of events. Man is deceiving himself when he sees anything "solid" in structures.
608.00 Stability: Necklace

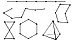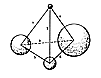
Fig. 608.01 		608.01 A necklace is unstable. The beads of a necklace may be superficially dissimilar, but they all have similar tubes running through them with the closed tension string leading through all the tubes. The simplest necklace would be one made only of externally undecorated tubes and of tubes all of the same length. As the overall shape of the necklace changes to any and all polygonal shapes and wavy drapings, we discover that the lengths of the beads in a necklace do not change. Only the angles between the tubes change. Therefore, stable refers only to angular invariability.
608.02 A six-edged polygon is unstable; it forms a drapable necklace. If we make a five-sided polygon, i.e., a pentagonal necklace, it is unstable. It, too, is a drapable necklace and is structurally unstable. Why? A necklace of three rigid tubes also has three flexible angle-accommodating tension joints. Here are six separate parts, each with its unique behavior characteristics which self-interfere to produce a stable pattern. How and why? We are familiar with the principle of lever advantage gained per length of lever arm from the fulcrum. We are familiar with the principle of the shears in which two levers share a common fulcrum, and the stronger and longer the shear arms, the more powerfully do they cut. Steel-bolt cutters have long lever arms.
608.03 In every triangle each comer angle tension connector serves as the common interfulcrum of the two push-pull, rigid lever arms comprising two of the three sides of the triangle adjacent to their respectively common angular corners; each pair of the triangle's tubular necklace sides, in respect to a given corner of the triangle, represent levers whose maximum-advantage ends are seized by the two ends of the third, rigid, push-pull, tubular side of the triangle, whose rigidity is imposed by its command of the two lever arm ends upon the otherwise flexible opposite angle. Thus we find that each of the necklace's triangular rigid tube sides stabilizes its opposite angle with minimum effort by controlling the ends of the two levers fulcrumed by that opposite tension fastening of the triangle. Thus we find the triangle to be not only the unique pattern-self-stabilizing, multienergied complex, but also accomplishing pattern stabilization at minimum effort, which behavior coincides with science's discovery of the omni-minimum-effort behavior of all physical Universe .
608.04 The six independent energy units of the triangle that interact to produce pattern stability are the only plural polygon-surrounding, energy-event complexes to produce stabilized patterns. (The necklace corners can be fastened together with three separate tension-connectors, instead of by the string running all the way through the tubes, wherefore the three rigid tubes and the three flexible tension connectors are six unique, independent, energy events.)
608.05 We may say that structure is a self-stabilizing, pattern-integrity complex. Only the triangle produces structure and structure means only triangle; and vice versa.
608.06 Since tension and compression always and only coexist (See Sec. 640) with first one at high tide and the other at low tide, and then vice versa, the necklace tubes are rigid with compression at visible high tide and tension at invisible low tide; and each of the tension-connectors has compression at invisible low tide and tension at visible high tide; ergo, each triangle has both a positive and a negative triangle congruently coexistent and each visible triangle is two triangles: one visible and one invisible.
608.07 Chain-linkage necklace structures take advantage of the triangulation of geodesic lines and permit us to encompass relatively large volumes with relatively low logistic investment. Slackened necklace geodesic spheres can be made as compactable as hairnets and self-motor-opened after being shot into orbit.
608.08 It is a synergetic characteristic of minimum structural systems (tetrahedra) that the system is not stable until the last strut is introduced. Redundancy cannot be determined by energetic observation of behaviors of single struts (beams or columns) or any chain-linkage of same, that are less than six in number, or less than tetrahedron.
608.10 Necklace Polygons and Necklace Polyhedra: Tetrahedral, octahedral, and icosahedral necklace structures are all stable. Necklace cubes, rhombic dodecahedra, pentadodecahedra, vector equilibria, and tetrakaidecahedra are all unstable. Only necklace- omnitriangulated, multifrequency geodesic spheres are stable structures, because they are based entirely on omnitriangulated tetra-, octa-, and icosahedral systems.
608.11 The number of vertexes of the omnitriangulated spherical tetra-, octa-, or icosahedral structures of multifrequency geodesic spheres corresponds exactly with the number of external layer spheres of closest-packed unit radius spherical agglomeration of tetrahedra, octahedra, or icosahedra:
Tetrahedra 2F2 + 2
Octahedra 4F2 + 2
Icosahedra 10F2 + 2
Only tetrahedral, octahedral, and icosahedral structural systems are stable, i.e., complete, nonredundant, self-stabilizing.
608.20 Even- and Odd-Number Reduction of Necklace Polygons

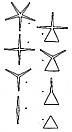Fig. 608.21 		608.21 We undertake experimental and progressive reduction of the tubularly beaded necklace's multipolygonal flexibility. The reduction is accomplished by progressive one-by-one elimination of tubes from the assembly. The progressive elimination alters the remaining necklace assemblage from a condition of extreme accommodation of contouring intimacies and drapability over complexedly irregular, multidimensional forms until the assembly gradually approaches a number of remaining tubes whose magnitude can be swiftly assessed without much conscious counting. As the multipolygonal assembly approaches a low-number magnitude of components of the polygons, it becomes recognizable that an even number of remaining tubes can be arranged in a symmetrical totality of inward-outward, inward-outward points, producing a corona or radiant starlike patterning, or the patterning of the extreme crests and troughs of a circular wave. When the number of tubular beads is odd, however, then the extra tube can only be accommodated by either a crest-to-crest or a trough-to-trough chord of the circle. This is the pattern of a gear with one odd double-space tooth in each circle. If the extra length is used to join two adjacent crests chordally, this tooth could mesh cyclically as a gear only with an equal number of similarly toothed gears of slightly larger diameter, where the extra length is used to interconnect the two adjacent troughs chordally. (See Fig. 608.21)
608.22 Even-numbered, equilength, tubular-bead necklaces can be folded into parallel bundles by slightly stretching the interconnection tension cable on which they are strung. Odd numbers cannot be so bundled.

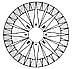Fig. 608.23 		608.23 Congruence with Mariner's Compass Rose: As the number of remaining tubes per circle become less than 40, certain patterns seem mildly familiar__as, for instance, that of the conventional draftsman's 360-degree, transparent-azimuth circle with its 36 main increments, each subdivided into 10 degrees. At the 32-tube level we have congruence with the mariner's compass rose, with its four cardinal points, each further subdivided by eight points (see Fig. 608.23).
608.24 Next in familiarity of the reduced numbers of circular division increments comes the 12 hours of the clock. Then the decimal system's azimuthal circle of 10 with 10 secondary divisions. Circles of nine are unfamiliar. But the octagon's division is highly familiar and quickly recognized. Septagons are not. Powerfully familiar and instantly recognized are the remaining hexagon, pentagon, square, and triangle. There is no twogon. Triangle is the minimum polygon. Triangle is the minimum-limit case.
608.25 All the necklace polygons prior to the triangle are flexibly drapable and omnidirectionally flexible with the sometimes-square-sometimes-diamond, four-tube necklace as the minimum-limit case of parallel bundling of the tubes. The triangle, being odd in number, cannot be bundled and thus remains not only the minimum polygon but the only inflexible, nonfoldable polygon.
608.30 Triangle as Minimum-altitude Tetrahedron
608.31 In Euclidean geometry triangles and other polygons were misinformedly thought of as occurring in two-dimensional planes. The substanceless, no-altitude, planar polygons were thought to hold their shape__as did any polygonal shape traced on the Earth's surface__ignoring the fact that the shape of any polygon of more than three edges is maintained only by the four-dimensional understructuring. Only the triangle has an inherent and integral structural integrity.
608.32 The triangular necklace is not two-dimensional, however; like all experienceable structural entities it is four-dimensional, as must be all experienceably realized polygonal models even though the beads are of chalk held together by the tensile coherence of the blackboard. Triangles at their simplest consist experientially of one minimum-altitude tetrahedron.
Next Section: 609.00
Copyright © 1997 Estate of R. Buckminster Fuller