 Tools of Geometry
Tools of Geometry

|
821.01
 The Early Greek geometers and their Egyptian and Babylonian
predecessors
pursued the science of geometry with three basic tools;
the dividers, the straightedge, and
the scriber. They established the first rule of the
game of geometry, that they could not
introduce information into their exploration unless
it was acquired empirically as
constructed by the use of those tools. With the progressive
interactive use of these three
tools, they produced modular areas, angles, and linear
spaces.
The Early Greek geometers and their Egyptian and Babylonian
predecessors
pursued the science of geometry with three basic tools;
the dividers, the straightedge, and
the scriber. They established the first rule of the
game of geometry, that they could not
introduce information into their exploration unless
it was acquired empirically as
constructed by the use of those tools. With the progressive
interactive use of these three
tools, they produced modular areas, angles, and linear
spaces.
|

|
821.02
 The basic flaw in their game was that they failed
to identify and define as a
tool the surface on which they inscribed. In absolute
reality, this surface constituted a
fourth tool absolutely essential to their demonstration.
The absolute error of this oversight
was missed at the time due to the minuscule size of
man in relation to his planet Earth.
While there were a few who conceived of Earth as a sphere,
they assumed that a local
planar condition existed__which the vast majority of
humans assumed to be extended to
infinity, with a four-cornered Earth plane surrounded
by the plane of water that went to
infinity.
The basic flaw in their game was that they failed
to identify and define as a
tool the surface on which they inscribed. In absolute
reality, this surface constituted a
fourth tool absolutely essential to their demonstration.
The absolute error of this oversight
was missed at the time due to the minuscule size of
man in relation to his planet Earth.
While there were a few who conceived of Earth as a sphere,
they assumed that a local
planar condition existed__which the vast majority of
humans assumed to be extended to
infinity, with a four-cornered Earth plane surrounded
by the plane of water that went to
infinity.
|

|
821.03
 They assumed the complementary tool to be a plane.
Because the plane went
to infinity in all planar directions, it could not be
defined and therefore was spontaneously
overlooked as a tool essential to their empirical demonstrating.
What they could not
define, yet obviously needed, they identified by the
ineffable title "axiomatic," meaning
"Everybody knows that." Had they recognized the essentiality
of defining the fourth tool
upon which they inscribed, and had they recognized that
our Earth was spherical__ergo,
finite; ergo, definite__they could and probably would
have employed strategies completely
different from that of their initiation of geometry
with the exclusive use of the plane. But
to the eastern Mediterranean world there lay the flat,
infinite plane of the Earth at their
feet on which to scratch with a scriber.
They assumed the complementary tool to be a plane.
Because the plane went
to infinity in all planar directions, it could not be
defined and therefore was spontaneously
overlooked as a tool essential to their empirical demonstrating.
What they could not
define, yet obviously needed, they identified by the
ineffable title "axiomatic," meaning
"Everybody knows that." Had they recognized the essentiality
of defining the fourth tool
upon which they inscribed, and had they recognized that
our Earth was spherical__ergo,
finite; ergo, definite__they could and probably would
have employed strategies completely
different from that of their initiation of geometry
with the exclusive use of the plane. But
to the eastern Mediterranean world there lay the flat,
infinite plane of the Earth at their
feet on which to scratch with a scriber.
|

|
821.10
 Dividers: The ends of two sticks can be bound together
to serve as dividers.
A straightedge stick could be whittled by a knife and
sighted for straightness and improved
by more whittling.
Dividers: The ends of two sticks can be bound together
to serve as dividers.
A straightedge stick could be whittled by a knife and
sighted for straightness and improved
by more whittling.
|

|
821.11
 The opening of the dividers could be fixed by binding
on a third stick
between the other two ends, thus rigidifying by triangulation.
Almost anyone at sea or in
the desert could start playing this game.
The opening of the dividers could be fixed by binding
on a third stick
between the other two ends, thus rigidifying by triangulation.
Almost anyone at sea or in
the desert could start playing this game.
|

|
825.00
 Greek Scribing of Right-Angle Modularity in a Plane
Greek Scribing of Right-Angle Modularity in a Plane
|
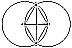 Fig. 825.01 |
825.01
 It was easy for the Greeks to use their fixed dividers
to identify two points
on the plane marked by the divider's two ends: A and
B, respectively. Employing their
straightedge, they could inscribe the line between these
two points, the line AB. Using one
end of the dividers as the pivot point at one end of
the line, A, a circle can be described
around the original line terminal: circle A. Using point
B as a center, a circle can be
described around it, which we will call circle B. These
two circles intersect one another at
two points on either side of the line AB. We will call
the intersection points C and C'.
It was easy for the Greeks to use their fixed dividers
to identify two points
on the plane marked by the divider's two ends: A and
B, respectively. Employing their
straightedge, they could inscribe the line between these
two points, the line AB. Using one
end of the dividers as the pivot point at one end of
the line, A, a circle can be described
around the original line terminal: circle A. Using point
B as a center, a circle can be
described around it, which we will call circle B. These
two circles intersect one another at
two points on either side of the line AB. We will call
the intersection points C and C'.
|

|
825.02
 By construction, they demonstrated that points C and
C' were both
equidistant from points A and B. In this process, they
have also defined two equilateral
triangles ABC and ABC', with a congruent edge along
the line AB and with points C and
C` equidistant on either side from points A and B, respectively.
By construction, they demonstrated that points C and
C' were both
equidistant from points A and B. In this process, they
have also defined two equilateral
triangles ABC and ABC', with a congruent edge along
the line AB and with points C and
C` equidistant on either side from points A and B, respectively.
|

|
825.10
 Right Triangle
Right Triangle
|

|
825.11
 They then used a straightedge to connect points C
and C' with a line that
they said bisected line AB perpendicularly, being generated
by equidistance from either
point on either side. Thus the Greeks arrived at their
right triangle; in fact, their four right
triangles. We will designate as point D the intersection
of the lines CC' and AB. This gave
the Greeks four angles around a common point. The four
right triangles ADC, BDC,
ADC', and BDC' have hypotenuses and legs that are, as
is apparent from even the most
casual inspection, of three different lengths. The leg
DB, for instance, is by equidistance
construction exactly one-half of AB, since AB was the
radius of the two original circles
whose circumferences ran through one another's centers.
By divider inspections, DB is
less than CD and CD is less than CB. The length of the
line CD is unknown in respect to
the original lines AB, BD, or AC, lines that represented
the original opening of the
dividers. They have established, however, with satisfaction
of the rules of their game, that
360 degrees of circular unity at D could be divided
into four equal 90-degree angles
entirely and evenly surrounding point D.
They then used a straightedge to connect points C
and C' with a line that
they said bisected line AB perpendicularly, being generated
by equidistance from either
point on either side. Thus the Greeks arrived at their
right triangle; in fact, their four right
triangles. We will designate as point D the intersection
of the lines CC' and AB. This gave
the Greeks four angles around a common point. The four
right triangles ADC, BDC,
ADC', and BDC' have hypotenuses and legs that are, as
is apparent from even the most
casual inspection, of three different lengths. The leg
DB, for instance, is by equidistance
construction exactly one-half of AB, since AB was the
radius of the two original circles
whose circumferences ran through one another's centers.
By divider inspections, DB is
less than CD and CD is less than CB. The length of the
line CD is unknown in respect to
the original lines AB, BD, or AC, lines that represented
the original opening of the
dividers. They have established, however, with satisfaction
of the rules of their game, that
360 degrees of circular unity at D could be divided
into four equal 90-degree angles
entirely and evenly surrounding point D.
|

|
825.20
 Hexagonal Construction
Hexagonal Construction
|

|
825.21
 Diameter: The Greeks then started another independent
investigation with
their three tools on the seemingly flat planar surface
of the Earth. Using their dividers to
strike a circle and using their straightedge congruent
to the center of the circle, they were
able with their scriber to strike a seemingly straight
line through the center of construction
of the circle. As the line passed out of the circle
in either direction from the center, it
seemingly could go on to infinity, and therefore was
of no further interest to them. But
inside the circle, as the line crossed the circumference
at two points on either side of its
center, they had the construction information that the
line equated the opening of the
dividers in two opposite directions. They called this
line the diameter: DIA + METER.
Diameter: The Greeks then started another independent
investigation with
their three tools on the seemingly flat planar surface
of the Earth. Using their dividers to
strike a circle and using their straightedge congruent
to the center of the circle, they were
able with their scriber to strike a seemingly straight
line through the center of construction
of the circle. As the line passed out of the circle
in either direction from the center, it
seemingly could go on to infinity, and therefore was
of no further interest to them. But
inside the circle, as the line crossed the circumference
at two points on either side of its
center, they had the construction information that the
line equated the opening of the
dividers in two opposite directions. They called this
line the diameter: DIA + METER.
|
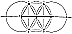 Fig. 825.22 |
825.22
 Now we will call the center of the constructed circle
D and the two
intersections of the line and the circumference A and
B. That AD = DB is proven by
construction. They know that any point on the circumference
is equidistant from D. Using
their dividers again and using point A as a pivot, they
drew a circle around A; they drew a
second circle using B as a pivot. Both of these circles
pass through D. The circle around A
intersects the circle around D at two points, C and
C'. The circle around B intersects the
circle around D at two points, E and E' . The circle
around A and the circle around B are
tangent to one another at the point D.
Now we will call the center of the constructed circle
D and the two
intersections of the line and the circumference A and
B. That AD = DB is proven by
construction. They know that any point on the circumference
is equidistant from D. Using
their dividers again and using point A as a pivot, they
drew a circle around A; they drew a
second circle using B as a pivot. Both of these circles
pass through D. The circle around A
intersects the circle around D at two points, C and
C'. The circle around B intersects the
circle around D at two points, E and E' . The circle
around A and the circle around B are
tangent to one another at the point D.
|

|
825.23
 They have now constructed four equilateral triangles
in two pairs: ADC and
ADC' as the first pair, and DBE and DBE' as the second
pair. They know that the lines
AC, CD, AC', and DC' are all identical in length, being
the fixed opening of the dividers
and so produced and proven by construction. The same
is true of the lines DE, EB, DE',
and BE'__they are all the same. The Greeks found it a
tantalizing matter that the two lines
CE and C'E', which lie between the vertexes of the two
pairs of equilateral triangles,
seemed to be equal, but there was no way for them to
prove it by their construction.
They have now constructed four equilateral triangles
in two pairs: ADC and
ADC' as the first pair, and DBE and DBE' as the second
pair. They know that the lines
AC, CD, AC', and DC' are all identical in length, being
the fixed opening of the dividers
and so produced and proven by construction. The same
is true of the lines DE, EB, DE',
and BE'__they are all the same. The Greeks found it a
tantalizing matter that the two lines
CE and C'E', which lie between the vertexes of the two
pairs of equilateral triangles,
seemed to be equal, but there was no way for them to
prove it by their construction.
|

|
825.24
 At first it seemed they might be able to prove that
the increments CE and
C'E' are not only equal to one another, but are equal
to the basic radius of the circle AD;
therefore, the hexagon ACEBE'C' would be an equilateral
hexagon; and hexagons would
be inherently subdivisible into six 60-degree equilateral
triangles around the central point,
and all the angles would be of 60 degrees.
At first it seemed they might be able to prove that
the increments CE and
C'E' are not only equal to one another, but are equal
to the basic radius of the circle AD;
therefore, the hexagon ACEBE'C' would be an equilateral
hexagon; and hexagons would
be inherently subdivisible into six 60-degree equilateral
triangles around the central point,
and all the angles would be of 60 degrees.
|

|
825.25
 There seemed to be one more chance for them to prove
this to be true,
which would have provided an equiangular, equiedged,
triangularly stable structuring of
areal mensuration. This last chance to prove it was
by first showing by construction that
the line ADB, which runs through the point of tangency
of the circles A and B, is a straight
line. This was constructed by the straightedge as the
diameter of circle D. This diameter is
divided by four equal half-radii, which are proven to
be half-radii by their perpendicular
intersection with lines both of whose two ends are equidistant
from two points on either
side of the intersecting lines. If it could be assumed
that: (1) the lines CE and C'E' were
parallel to the straight line ADB running through the
point of tangency as well as
perpendicular to both the lines CC' and EE'; and (2)
if it could be proven that when one
end between two parallels is perpendicular to one of
the parallels, the other end is
perpendicular to the other parallel; and (3) if it could
be proven also that the perpendicular
distances between any two parallels were always the
same, they could then have proven
CE = CD = DE = D'E', and their hexagon would be equilateral
and equiradial with radii
and chords equal.
There seemed to be one more chance for them to prove
this to be true,
which would have provided an equiangular, equiedged,
triangularly stable structuring of
areal mensuration. This last chance to prove it was
by first showing by construction that
the line ADB, which runs through the point of tangency
of the circles A and B, is a straight
line. This was constructed by the straightedge as the
diameter of circle D. This diameter is
divided by four equal half-radii, which are proven to
be half-radii by their perpendicular
intersection with lines both of whose two ends are equidistant
from two points on either
side of the intersecting lines. If it could be assumed
that: (1) the lines CE and C'E' were
parallel to the straight line ADB running through the
point of tangency as well as
perpendicular to both the lines CC' and EE'; and (2)
if it could be proven that when one
end between two parallels is perpendicular to one of
the parallels, the other end is
perpendicular to the other parallel; and (3) if it could
be proven also that the perpendicular
distances between any two parallels were always the
same, they could then have proven
CE = CD = DE = D'E', and their hexagon would be equilateral
and equiradial with radii
and chords equal.
|

|
825.26
 Pythagorean Proof
Pythagorean Proof
|

|
825.261
 All of these steps were eventually taken and proven
in a complex of other
proofs. In the meantime, they were diverted by the Pythagoreans'
construction proof of
"the square of the hypotenuse of a right triangle's
equatability with the sum of the squares
of the other two sides," and the construction proof
that any non-right triangle's
dimensional values could be obtained by dropping a perpendicular
upon one of its sides
from one of its vertexes and thus converting it into
two right triangles each of which could
be solved arithmetically by the Pythagoreans' "squares"
without having to labor further
with empirical constructs. This arithmetical facility
induced a detouring of strictly
constructional explorations, hypotheses, and proofs
thereof.
All of these steps were eventually taken and proven
in a complex of other
proofs. In the meantime, they were diverted by the Pythagoreans'
construction proof of
"the square of the hypotenuse of a right triangle's
equatability with the sum of the squares
of the other two sides," and the construction proof
that any non-right triangle's
dimensional values could be obtained by dropping a perpendicular
upon one of its sides
from one of its vertexes and thus converting it into
two right triangles each of which could
be solved arithmetically by the Pythagoreans' "squares"
without having to labor further
with empirical constructs. This arithmetical facility
induced a detouring of strictly
constructional explorations, hypotheses, and proofs
thereof.
|

|
825.27
 Due to their misassumed necessity to commence their
local scientific
exploration of geometry only in a supposed plane that
extended forever without definable
perimeter, that is, to infinity, the Ionians began using
their right-triangle exploration before
they were able to prove that six equilateral triangles
lie in a circle around point D. They
could divide the arithmetical 360 degrees of circular
unity agreed upon into six 60-degree
increments. And, as we have already noted, if this had
been proven by their early
constructions with their three tools, they might then
have gone on to divide all planar
space with equilateral triangles, which models would
have been very convenient in
connection with the economically satisfactory point-locating
capability of triangulation and
trigonometry.
Due to their misassumed necessity to commence their
local scientific
exploration of geometry only in a supposed plane that
extended forever without definable
perimeter, that is, to infinity, the Ionians began using
their right-triangle exploration before
they were able to prove that six equilateral triangles
lie in a circle around point D. They
could divide the arithmetical 360 degrees of circular
unity agreed upon into six 60-degree
increments. And, as we have already noted, if this had
been proven by their early
constructions with their three tools, they might then
have gone on to divide all planar
space with equilateral triangles, which models would
have been very convenient in
connection with the economically satisfactory point-locating
capability of triangulation and
trigonometry.
|

|
825.28
 Euclid was not trying to express forces. We, however__inspired
by
Avogadro's identical-energy conditions under which different
elements disclosed the same
number of molecules per given volume__are exploring the
possible establishment of an
operationally strict vectorial geometry field, which
is an isotropic (everywhere the same)
vector matrix. We abandon the Greek perpendicularity
of construction and find ourselves
operationally in an omnidirectional, spherically observed,
multidimensional, omni-
intertransforming Universe. Our first move in spherical
reality scribing is to strike a quasi-
sphere as the vectorial radius of construction. Our
dividers are welded at a fixed angle.
The second move is to establish the center. Third move:
a surface circle. The radius is
uniform and the lesser circle is uniform. From the triangle
to the tetrahedron, the dividers
go to direct opposites to make two tetrahedra with a
common vertex at the center. Two
tetrahedra have six internal faces=hexagon=genesis of
bow tie=genesis of
modelability=vector equilibrium. Only the dividers and
straightedge are used. You start
with two events__any distance apart: only one module
with no subdivision; ergo, timeless;
ergo, eternal; ergo, no frequency. Playing the game
in a timeless manner. (You have to
have division of the line to have frequency, ergo, to
have time.) (See Secs.
420
and
650.)
Euclid was not trying to express forces. We, however__inspired
by
Avogadro's identical-energy conditions under which different
elements disclosed the same
number of molecules per given volume__are exploring the
possible establishment of an
operationally strict vectorial geometry field, which
is an isotropic (everywhere the same)
vector matrix. We abandon the Greek perpendicularity
of construction and find ourselves
operationally in an omnidirectional, spherically observed,
multidimensional, omni-
intertransforming Universe. Our first move in spherical
reality scribing is to strike a quasi-
sphere as the vectorial radius of construction. Our
dividers are welded at a fixed angle.
The second move is to establish the center. Third move:
a surface circle. The radius is
uniform and the lesser circle is uniform. From the triangle
to the tetrahedron, the dividers
go to direct opposites to make two tetrahedra with a
common vertex at the center. Two
tetrahedra have six internal faces=hexagon=genesis of
bow tie=genesis of
modelability=vector equilibrium. Only the dividers and
straightedge are used. You start
with two events__any distance apart: only one module
with no subdivision; ergo, timeless;
ergo, eternal; ergo, no frequency. Playing the game
in a timeless manner. (You have to
have division of the line to have frequency, ergo, to
have time.) (See Secs.
420
and
650.)
|

|
825.29
 Commencing proof upon a sphere as representative of
energy convergent or
divergent, we may construct an equilateral triangle
from any point on the surface. If we
describe equilateral (equiangular) triangles whose chords
are identical to the radii, the
same sphere may be intersected alternately by four great-circle
planes whose circles
intercept each other, respectively, at 12 equidistant
points in such a manner that only two
circles intersect at any one point. As this system is
described, each great circle becomes
symmetrically subdivided into six equal-arc segments
whose chords are identical to the
radii. From this four-dimensional tribisection, any
geometrical form may be described in
whole fractions.
Commencing proof upon a sphere as representative of
energy convergent or
divergent, we may construct an equilateral triangle
from any point on the surface. If we
describe equilateral (equiangular) triangles whose chords
are identical to the radii, the
same sphere may be intersected alternately by four great-circle
planes whose circles
intercept each other, respectively, at 12 equidistant
points in such a manner that only two
circles intersect at any one point. As this system is
described, each great circle becomes
symmetrically subdivided into six equal-arc segments
whose chords are identical to the
radii. From this four-dimensional tribisection, any
geometrical form may be described in
whole fractions.
|

|
825.30
 Two-Way Rectilinear Grid
Two-Way Rectilinear Grid
|

|
825.31
 To the Greeks, a two-way, rectilinearly intersecting
grid of parallel lines
seemed simpler than would a three-way grid of parallel
lines. (See Chapter 11, "Projective
Transformation.") And the two-way grid was highly compatible
with their practical
coordinate needs for dealing with an assumedly flat-plane
Universe. Thus the Greeks came
to employ 90-degreeness and unique perpendicularity
to the system as a basic additional
dimensional requirement for the exclusive, and consequently
unchallenged, three-
dimensional geometrical data coordination.
To the Greeks, a two-way, rectilinearly intersecting
grid of parallel lines
seemed simpler than would a three-way grid of parallel
lines. (See Chapter 11, "Projective
Transformation.") And the two-way grid was highly compatible
with their practical
coordinate needs for dealing with an assumedly flat-plane
Universe. Thus the Greeks came
to employ 90-degreeness and unique perpendicularity
to the system as a basic additional
dimensional requirement for the exclusive, and consequently
unchallenged, three-
dimensional geometrical data coordination.
|

|
825.32
 Their arithmetical operations were coordinated with
geometry on the
assumption that first-power numbers represented linear
module tallies, that second-power
N2 = square increments, and that third-power N3 = cubical
increments of space. First
dimension was length expressed with one line. Two dimensions
introduced width
expressed with a cross of two lines in a plane. Three
dimensions introduced height
expressed by a third line crossing perpendicularly to
the first two at their previous
crossing, making a three-way, three-dimensional cross,
which they referred to as the XYZ
coordinate system. The most economical distance measuring
between the peripheral points
of such XYZ systems involved hypotenuses and legs of
different lengths. This three-
dimensionality dominated the 2,000-year scientific development
of the XYZ__c.gts.
"Comprehensive Coordinate System of Scientific Mensurations."
As a consequence,
identifications of physical reality have been and as
yet are only awkwardly characterized
because of the inherent irrationality of the peripheral
hypotenuse aspects of systems in
respect to their radial XYZ interrelationships.
Their arithmetical operations were coordinated with
geometry on the
assumption that first-power numbers represented linear
module tallies, that second-power
N2 = square increments, and that third-power N3 = cubical
increments of space. First
dimension was length expressed with one line. Two dimensions
introduced width
expressed with a cross of two lines in a plane. Three
dimensions introduced height
expressed by a third line crossing perpendicularly to
the first two at their previous
crossing, making a three-way, three-dimensional cross,
which they referred to as the XYZ
coordinate system. The most economical distance measuring
between the peripheral points
of such XYZ systems involved hypotenuses and legs of
different lengths. This three-
dimensionality dominated the 2,000-year scientific development
of the XYZ__c.gts.
"Comprehensive Coordinate System of Scientific Mensurations."
As a consequence,
identifications of physical reality have been and as
yet are only awkwardly characterized
because of the inherent irrationality of the peripheral
hypotenuse aspects of systems in
respect to their radial XYZ interrelationships.
|

|
825.33
 Commanded by their wealth-controlling patrons, pure
scientists have had to
translate their theoretical calculations of physical-system
behaviors into coordinate
relationship with physical reality in order to permit
applied science to reduce theoretical
inventions to physical practice and use. All of the
analytic geometers and calculus
mathematicians identify their calculus-derived coordinate
behaviors of theoretical systems
only in terms of linear measurements taken outwardly
from central points of reference;
they locate the remote event points relative to those
centers only by an awkward set of
perpendicularities emanating from, and parallel to,
the central XYZ grid of perpendicular
coordinates. The irrationality of this peripheral measuring
in respect to complexedly
orbited atomic nuclei has occasioned the exclusively
mathematical processing of energy
data without the use of conceptual models.
Commanded by their wealth-controlling patrons, pure
scientists have had to
translate their theoretical calculations of physical-system
behaviors into coordinate
relationship with physical reality in order to permit
applied science to reduce theoretical
inventions to physical practice and use. All of the
analytic geometers and calculus
mathematicians identify their calculus-derived coordinate
behaviors of theoretical systems
only in terms of linear measurements taken outwardly
from central points of reference;
they locate the remote event points relative to those
centers only by an awkward set of
perpendicularities emanating from, and parallel to,
the central XYZ grid of perpendicular
coordinates. The irrationality of this peripheral measuring
in respect to complexedly
orbited atomic nuclei has occasioned the exclusively
mathematical processing of energy
data without the use of conceptual models.
|
| Next Section: 826.00 |