 Isotropic Vector Matrix
Isotropic Vector Matrix
420.00  Isotropic Vector Matrix
Isotropic Vector Matrix
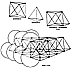 Fig. 420.01 |
420.01
 When the centers of equiradius spheres in closest
packing are joined by most
economical lines, i.e., by geodesic vectorial lines,
an isotropic vector matrix is disclosed__
"isotropic" meaning "everywhere the same," "isotropic
vector" meaning "everywhere the
same energy conditions." This matrix constitutes an
array of equilateral triangles that
corresponds with the comprehensive coordination of nature's
most economical, most
comfortable, structural interrelationships employing
60-degree association and
disassociation. Remove the spheres and leave the vectors,
and you have the octahedron-
tetrahedron complex, the octet truss, the isotropic
vector matrix. (See Secs. 650 and
825.28.)
When the centers of equiradius spheres in closest
packing are joined by most
economical lines, i.e., by geodesic vectorial lines,
an isotropic vector matrix is disclosed__
"isotropic" meaning "everywhere the same," "isotropic
vector" meaning "everywhere the
same energy conditions." This matrix constitutes an
array of equilateral triangles that
corresponds with the comprehensive coordination of nature's
most economical, most
comfortable, structural interrelationships employing
60-degree association and
disassociation. Remove the spheres and leave the vectors,
and you have the octahedron-
tetrahedron complex, the octet truss, the isotropic
vector matrix. (See Secs. 650 and
825.28.)
|
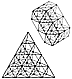 Fig. 420.02 |
420.02
 The isotropic vector matrix is four-dimensional and
60-degree coordinated. It
provides an omnirational accounting system that, if
arbitrarily accounted on a three-
dimensional, 90-degree basis, becomes inherently irrational.
The isotropic vector matrix
demonstrates the ability of the symmetrically and asymmetrically
terminaled, high-
frequency energy vectors to accommodate the structuring
of any shape. (See Sec. 923.)
The isotropic vector matrix is four-dimensional and
60-degree coordinated. It
provides an omnirational accounting system that, if
arbitrarily accounted on a three-
dimensional, 90-degree basis, becomes inherently irrational.
The isotropic vector matrix
demonstrates the ability of the symmetrically and asymmetrically
terminaled, high-
frequency energy vectors to accommodate the structuring
of any shape. (See Sec. 923.)
|

|
420.03
 Our extension of the Avogadro hypothesis
(Sec. 410)
generalizes that all
energy conditions are the same. Inasmuch as vectors
describe energy conditions, this
would mean a volumetric aggregation of vectors in a
structural complex in which all of the
interacting vectors would have to be of the same length
and all of their intersecting angles
would have to be the same. This state of omnisameness
of vectors stipulates the
"isotropic," meaning everywhere the same. This prescribes
an everywhere state of
equilibrium.
Our extension of the Avogadro hypothesis
(Sec. 410)
generalizes that all
energy conditions are the same. Inasmuch as vectors
describe energy conditions, this
would mean a volumetric aggregation of vectors in a
structural complex in which all of the
interacting vectors would have to be of the same length
and all of their intersecting angles
would have to be the same. This state of omnisameness
of vectors stipulates the
"isotropic," meaning everywhere the same. This prescribes
an everywhere state of
equilibrium.
|

|
420.04
 Equilibrium
Equilibrium
|

|
420.041
 Nature is said to abhor an equilibrium as much as she
abhors a perfect
vacuum or a perfect anything. Heisenberg's indeterminism
and quasiprecision mechanics'
recognition of inherent inaccuracy of observation or
articulation seems to suggest that the
asymmetric deviations and aberrations relative to equilibrium
are inherent in the
imperfection of a limited life of humans with a tightly
limited range of perceptible
differentiation of details of its experience. Nature
demonstrates her abhorrence of
equilibrium when an airplane in flight slows to a speed
that reduces the airfoil "lift" and
brings the airplane's horizontal flight forces into
equilibrium with Earth gravity's vertically
Earthward pull. The plane is said then to stall, at
which moment the plane's indeterminate
direction makes it unmanageable because the rudder and
elevator surfaces lack enough
passing air to provide steerability, and the plane goes
swiftly through equilibrium and into
an Earthward-spinning plunge. Despite the untenability
of equilibrium, it seemed to me
that we could approach or employ it referentially as
we employed a crooked line__the
deliberately nonstraight
(see Sec. 522)
line that approaches
but never reaches the perfect
or exact. A comprehensive energy system could employ
the positive and negative
pulsations and intertransformative tendencies of equilibrium.
The vector equilibrium
became the logical model of such omnidimensional, omniexperience-accommodation
studies. Because we have learned that scientists have
experimental evidence only of waves
and wavilinearity and no evidence of straight lines,
it became evident that the radial and
circumferential vectors of the vector equilibrium must
be wavilinear, which meant that as
coil springs when compressioned will lessen in length
and when tensed will be increased in
length__ergo, the explosive disintegrative radial forces
of Universe would compress and
lessen in outward disintegrative length and would be
well inside the closed-back-on-itself,
hexagonally tensed, embracing vectors, indicating a
higher effectiveness of tensile integrity
of Universe over any locally disintegrative forces.
The comprehensive vector-equilibrium
system would also have to recognize all the topological
interpatterning characteristics and
components; also, as a quasi-equilibrious system, all
of its structural component vectors
would have to be approximately the same length; therefore,
all the interangulation would
have to be in aberration increments relative to 60 degrees
as the equilibrious norm.
Nature is said to abhor an equilibrium as much as she
abhors a perfect
vacuum or a perfect anything. Heisenberg's indeterminism
and quasiprecision mechanics'
recognition of inherent inaccuracy of observation or
articulation seems to suggest that the
asymmetric deviations and aberrations relative to equilibrium
are inherent in the
imperfection of a limited life of humans with a tightly
limited range of perceptible
differentiation of details of its experience. Nature
demonstrates her abhorrence of
equilibrium when an airplane in flight slows to a speed
that reduces the airfoil "lift" and
brings the airplane's horizontal flight forces into
equilibrium with Earth gravity's vertically
Earthward pull. The plane is said then to stall, at
which moment the plane's indeterminate
direction makes it unmanageable because the rudder and
elevator surfaces lack enough
passing air to provide steerability, and the plane goes
swiftly through equilibrium and into
an Earthward-spinning plunge. Despite the untenability
of equilibrium, it seemed to me
that we could approach or employ it referentially as
we employed a crooked line__the
deliberately nonstraight
(see Sec. 522)
line that approaches
but never reaches the perfect
or exact. A comprehensive energy system could employ
the positive and negative
pulsations and intertransformative tendencies of equilibrium.
The vector equilibrium
became the logical model of such omnidimensional, omniexperience-accommodation
studies. Because we have learned that scientists have
experimental evidence only of waves
and wavilinearity and no evidence of straight lines,
it became evident that the radial and
circumferential vectors of the vector equilibrium must
be wavilinear, which meant that as
coil springs when compressioned will lessen in length
and when tensed will be increased in
length__ergo, the explosive disintegrative radial forces
of Universe would compress and
lessen in outward disintegrative length and would be
well inside the closed-back-on-itself,
hexagonally tensed, embracing vectors, indicating a
higher effectiveness of tensile integrity
of Universe over any locally disintegrative forces.
The comprehensive vector-equilibrium
system would also have to recognize all the topological
interpatterning characteristics and
components; also, as a quasi-equilibrious system, all
of its structural component vectors
would have to be approximately the same length; therefore,
all the interangulation would
have to be in aberration increments relative to 60 degrees
as the equilibrious norm.
|

|
420.05
 The closest-packing-of-spheres model coincides with
the observed real
world's atomic packing of like atoms with their own
counterparts.
The closest-packing-of-spheres model coincides with
the observed real
world's atomic packing of like atoms with their own
counterparts.
|

|
420.06
 We find that the space compartmentation formed by
the vectors connecting
the sphere centers always consists only of tetrahedra
and octahedra. The spheres in closest
packing coincide with the Eulerian vertexes; the vectors
between the sphere centers are
the Eulerian edges; and the triangles so formed are
the "faces."
We find that the space compartmentation formed by
the vectors connecting
the sphere centers always consists only of tetrahedra
and octahedra. The spheres in closest
packing coincide with the Eulerian vertexes; the vectors
between the sphere centers are
the Eulerian edges; and the triangles so formed are
the "faces."
|

|
420.07
 All of the polygons formed by the interacting vectors
of the isotropic vector
matrix consist entirely of equilateral triangles and
squares. The squares occur as equatorial
cross sections of the octahedra. The triangles occur
as the external facets of both the
tetrahedra and the octahedra.
All of the polygons formed by the interacting vectors
of the isotropic vector
matrix consist entirely of equilateral triangles and
squares. The squares occur as equatorial
cross sections of the octahedra. The triangles occur
as the external facets of both the
tetrahedra and the octahedra.
|

|
420.08
 All the polygons are reducible to triangles and are
not further reducible. All
polyhedra are reducible to triangulation, i.e., to trusses
and are not further reducible.
Infinite polyhedra are infinitely faceted by basic trusses.
All the polygons are reducible to triangles and are
not further reducible. All
polyhedra are reducible to triangulation, i.e., to trusses
and are not further reducible.
Infinite polyhedra are infinitely faceted by basic trusses.
|

|
421.00
 Function of Nucleus in Isotropic Vector Matrix
Function of Nucleus in Isotropic Vector Matrix
|

|
421.01
 Because the spacing of absolutely compacted spheres
is tangential and
hexagonal in great-circle cross section around any one
sphere, the contact points are
always spaced equidistant from the centers of the spheres
and from their immediately
neighboring points, respectively; wherefore the dimensions
of a system of lines joining
each and all adjacent spherical centers are identical
to the universal radii of the identical
spheres and, therefore, to each other. Such a universal
system of identically dimensioned
lines, growing outwardly from any one nuclear vertex,
constitutes a universal vector
system in dynamic equilibrium, for all the force lines
are of equal magnitude.
Because the spacing of absolutely compacted spheres
is tangential and
hexagonal in great-circle cross section around any one
sphere, the contact points are
always spaced equidistant from the centers of the spheres
and from their immediately
neighboring points, respectively; wherefore the dimensions
of a system of lines joining
each and all adjacent spherical centers are identical
to the universal radii of the identical
spheres and, therefore, to each other. Such a universal
system of identically dimensioned
lines, growing outwardly from any one nuclear vertex,
constitutes a universal vector
system in dynamic equilibrium, for all the force lines
are of equal magnitude.
|

|
421.02
 In the isotropic vector matrix, every vector leads
from one nuclear center to
another, and therefore represents the operational effect
of a merging of any two or more
force centers upon each other. Each vector is composed
of two halves, each half
belonging respectively to any two adjacent nuclear centers
Each half of the
interconnecting vectors represents the radius of one
of the two spheres tangent to one
another at the vector midpoints.
In the isotropic vector matrix, every vector leads
from one nuclear center to
another, and therefore represents the operational effect
of a merging of any two or more
force centers upon each other. Each vector is composed
of two halves, each half
belonging respectively to any two adjacent nuclear centers
Each half of the
interconnecting vectors represents the radius of one
of the two spheres tangent to one
another at the vector midpoints.
|

|
421.03
 Unity as represented by the internuclear vector modulus
is of necessity
always of the value of two, for it represents union
of a minimum of two energy centers.
(See Sec. 240.40.)
Unity as represented by the internuclear vector modulus
is of necessity
always of the value of two, for it represents union
of a minimum of two energy centers.
(See Sec. 240.40.)
|

|
421.031
 Function of Nucleus in Isotropic Vector Matrix: Every
vector has two
ends both of which join with other vectors to produce
both structural systems and total
cosmic integrity of regeneration. Every vector unites
two ends.
Function of Nucleus in Isotropic Vector Matrix: Every
vector has two
ends both of which join with other vectors to produce
both structural systems and total
cosmic integrity of regeneration. Every vector unites
two ends.
|

|
421.04
 Each nuclear ball can have a neutral function among
the aggregates. It is a
nuclear ball whether it is in a planar array or in an
omnidirectional array. It has a unique
function in each of the adjacent systems that it bonds.
Each nuclear ball can have a neutral function among
the aggregates. It is a
nuclear ball whether it is in a planar array or in an
omnidirectional array. It has a unique
function in each of the adjacent systems that it bonds.
|

|
421.05
 The nucleus can accommodate wave passage without disrupting
the
fundamental resonance of the octaves. The tetrahedron
is the minimum, ergo prime, non-
nucleated structural system of Universe. The vector
equilibrium is the minimum, ergo
prime, nucleated structural system of Universe.
The nucleus can accommodate wave passage without disrupting
the
fundamental resonance of the octaves. The tetrahedron
is the minimum, ergo prime, non-
nucleated structural system of Universe. The vector
equilibrium is the minimum, ergo
prime, nucleated structural system of Universe.
|

|
421.10
 Corollary: Identically dimensioned nuclear systems
and layer growths occur
alike, relative to each and every absolutely compacted
sphere of the isotropic vector
matrix conglomerate, wherefore the integrity of the
individual energy center is
mathematically demonstrated to be universal both potentially
and kinetically
(Sec. 240.50).
Corollary: Identically dimensioned nuclear systems
and layer growths occur
alike, relative to each and every absolutely compacted
sphere of the isotropic vector
matrix conglomerate, wherefore the integrity of the
individual energy center is
mathematically demonstrated to be universal both potentially
and kinetically
(Sec. 240.50).
|

|
421.20
 Ideal Vectorial Geometry of Nucleated Systems
Ideal Vectorial Geometry of Nucleated Systems
|

|
421.21
 It is experientially suggested that the structural
interpatterning principles
apparently governing all atomic associability behaviors
are characterized by triangular and
tetrahedral accommodation, wherein the tetrahedron's
six positive and six negative
vectorial edge forces match a total of 12 universal
degrees of freedom. The tetrahedron's
exclusively edge-congruent-agglomeratability around
any one nuclear point produces the
vector equilibrium. These structural, pattern-governing,
conceptualizable principles in turn
govern all eternally regenerative design evolution,
including the complex patterning of
potential, symmetrically and asymmetrically limited,
pulsative regenerations, only in
respect to all of which are ideas conceivable. These
patternings are experientially manifest
in synergetics' closed-system topological hierarchy
through which we can explore the
ramifications of the idealistic vectorial geometry characteristics
of inherently nucleated
systems and their experientially demonstrable properties.
(For possible relevance to the
periodic table of the elements see
Sec. 955.30.)
It is experientially suggested that the structural
interpatterning principles
apparently governing all atomic associability behaviors
are characterized by triangular and
tetrahedral accommodation, wherein the tetrahedron's
six positive and six negative
vectorial edge forces match a total of 12 universal
degrees of freedom. The tetrahedron's
exclusively edge-congruent-agglomeratability around
any one nuclear point produces the
vector equilibrium. These structural, pattern-governing,
conceptualizable principles in turn
govern all eternally regenerative design evolution,
including the complex patterning of
potential, symmetrically and asymmetrically limited,
pulsative regenerations, only in
respect to all of which are ideas conceivable. These
patternings are experientially manifest
in synergetics' closed-system topological hierarchy
through which we can explore the
ramifications of the idealistic vectorial geometry characteristics
of inherently nucleated
systems and their experientially demonstrable properties.
(For possible relevance to the
periodic table of the elements see
Sec. 955.30.)
|

|
422.00
 Octet Truss
Octet Truss
|

|
422.01
 In an isotropic vector matrix, there are only two
clear-space polyhedra
described internally by the configuration of interacting
vectors: these are the regular
tetrahedron and the regular octahedron operating as
complementary space fillers. The
single octahedron-tetrahedron deep truss system is known
in synergetics as the octet truss.
In an isotropic vector matrix, there are only two
clear-space polyhedra
described internally by the configuration of interacting
vectors: these are the regular
tetrahedron and the regular octahedron operating as
complementary space fillers. The
single octahedron-tetrahedron deep truss system is known
in synergetics as the octet truss.
|

|
422.02
 The octet truss, or the isotropic vector matrix, is
generated by the
asymmetrical closest-packed sphere conglomerations.
The nuclei are incidental.
The octet truss, or the isotropic vector matrix, is
generated by the
asymmetrical closest-packed sphere conglomerations.
The nuclei are incidental.
|

|
422.03
 When four tetrahedra of a given size are symmetrically
intercombined by
single bonding, each tetrahedron will have one of its
four vertexes uncombined, and three
combined with the six mutually combined vertexes symmetrically
embracing to define an
octahedron; while the four noncombined vertexes of the
tetrahedra will define a
tetrahedron twice the edge length of the four tetrahedra
of given size; wherefore the
resulting central space of the double-size tetrahedron
is an octahedron. Together, these
polyhedra comprise a common octahedron-tetrahedron system.
When four tetrahedra of a given size are symmetrically
intercombined by
single bonding, each tetrahedron will have one of its
four vertexes uncombined, and three
combined with the six mutually combined vertexes symmetrically
embracing to define an
octahedron; while the four noncombined vertexes of the
tetrahedra will define a
tetrahedron twice the edge length of the four tetrahedra
of given size; wherefore the
resulting central space of the double-size tetrahedron
is an octahedron. Together, these
polyhedra comprise a common octahedron-tetrahedron system.
|

|
422.04
 The tetrahedronated octahedron and all other regular
symmetrical polyhedra
known are described repetitiously by compounding two
types of rational fraction
asymmetric elements of the tetrahedron and octahedron.
These elements are known in
synergetics as the A and B Quanta Modules. (See Sec.
920.)
The tetrahedronated octahedron and all other regular
symmetrical polyhedra
known are described repetitiously by compounding two
types of rational fraction
asymmetric elements of the tetrahedron and octahedron.
These elements are known in
synergetics as the A and B Quanta Modules. (See Sec.
920.)
|

|
422.10
 Force Distribution: In the three-way grid octet truss
system, concentrated
energy loads applied to any one point are distributed
radially outward in nine directions
and are immediately diffused into the finite hexagonally
arranged six vectors entirely
enclosing the six-way-distributed force. Each of the
hexagon's six vertexes distribute the
loads 18 ways to the next outwardly encircling vectors,
which progressively diffusing
system ultimately distributes the original concentrated
energy force equally to all parts of
the system as with a pneumatic tire. Thus the system
joins together synergetically to
distribute and inhibit the forces.
Force Distribution: In the three-way grid octet truss
system, concentrated
energy loads applied to any one point are distributed
radially outward in nine directions
and are immediately diffused into the finite hexagonally
arranged six vectors entirely
enclosing the six-way-distributed force. Each of the
hexagon's six vertexes distribute the
loads 18 ways to the next outwardly encircling vectors,
which progressively diffusing
system ultimately distributes the original concentrated
energy force equally to all parts of
the system as with a pneumatic tire. Thus the system
joins together synergetically to
distribute and inhibit the forces.
|

|
422.20
 Geometry of Structure: Considered solely as geometry
of structure, the
final identification of the octet truss by the chemists
and physicists as closest packing also
identifies the octet truss and vector equilibria structuring
as amongst the prime cosmic
principles permeating and facilitating all physical
experience.
Geometry of Structure: Considered solely as geometry
of structure, the
final identification of the octet truss by the chemists
and physicists as closest packing also
identifies the octet truss and vector equilibria structuring
as amongst the prime cosmic
principles permeating and facilitating all physical
experience.
|
| Next Section: 423.00 |