826.00 Unity of Peripheral and Radial Modularity
826.01 Had the Greeks originally employed a universal model of x-dimensional reality as their first tool upon and within which they could further inscribe and measure with their divider, scriber, and straightedge, they would have been able to arrive at unity of circumferential as well as radial modularity. This would have been very convenient to modern physics because all the accelerations of all the constantly transforming physical events of Universe are distinguished by two fundamentally different forms of acceleration, angular and linear.

Fig. 826.02 		826.02 Hammer Throw: When a man accelerates a weight on the end of a cord by swinging it around his head, the weight is restrained by the cord and it accumulates the energy of his exertions in the velocity it maintains in a circular pattern. This is angular acceleration, and its velocity rates and angular momentum are calculated in central-angle increments of the circular movement accomplished within given units of time. When the weight's cord is released by its human accelerator, it then goes into linear acceleration and its accomplished distance is measured in time increments following its release and its known release velocity, which calculations are modified by any secondary restraints.

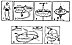Fig. 826.02A 		826.02A Hammer Throw: The picture of the hammer throw and gyroscope appearing in Synergetics 1 was incomplete, The complete sequence of six line drawings appears here in revised Fig. 826.02A.
826.03 The angular accelerations relate then to the myriad of circular or elliptical orbitings of components of systems around their respective centers or focii, and are intimate to original acceleration-generating factors such as the "hammer thrower" himself and his muscle as the metabolic powering by the beef he ate the day before, which gained its energy from vegetation it had eaten, which gained its energy from the Sun's radiation by photosynthesis- all of whose attendant relative efficiencies of energy relaying were consequent upon the relative design efficacies and energy divergence to complementary environment conditions of the total synergetically effective system with the eventually total regenerative Universe itself.3

(Footnote 3: This is a typical illustration of total energy accounting, which all society must become conversant with in short order if we are to pass through the crisis and flourish upon our planet. If we do suceed, it will be because, among other planetary events, humans will have come to recognize that the common wealth equating accounting must be one that locks fundamental and central energy incrementations--such as kilowatts hours--to human physical-energy work capability and its augmentation by the mind-comprehending employability of generalized principles of Universe, as these may be realistically appraised in the terms of increasing numbers of days for increasing hours and distances of increasing freedoms for increasing numbers of human beings. All of this fundamental data can be introduced into world computer memories, which can approximately instantly enlighten world humanity on its increasingly more effective options of evolutionary cooperation and fundamentally spontaneous social commitment.)
826.04 Science as a Tool: The linear measurements represent the radial going-away accelerations or resultants of earlier or more remote events as well as of secondary restraints. The rigid rectilinear angularity of the 90-degree-central-angle XYZ mensuration instituted by the Greeks made impossible any unit language of direct circumferential or peripheral coordination between angular and linear phenomena. As a consequence, only the radial and linear measurements have been available to physics. For this reason, physics has been unable to make simultaneous identification of both wave and particle aspects of energy events.
826.05 The Greeks' planar inception of geometry and its diversion first into theoretical mathematical calculations and ultimate abandonment of models has occasioned the void of ignorance now existing between the sciences and the humanities imposed by the lack of logical and unitarily moduled conceptual systems. This, in turn, has occasioned complete social blindness to either the facts or the potential benefits of science to humanity. Thus science has now come to represent an invisible monster to vast numbers of society, wherefore society threatens to jettison science and its "obnoxious" technology, not realizing that this would lead swiftly to genocide. Central to this crisis of terrestrially situate humans is the necessity for discovering and employing a comprehensively comprehendible universal coordinate system that will make it swiftly lucid to world society that science and technology are only manipulative tools like inanimate and cut-offable hands which may be turned to structuring or destructuring. How they are to be employed is not a function of the tools but of human choice. The crisis is one of the loving and longing impulse to understand and be understood, which results as informed comprehension. It is the will to structure versus ignorant yielding to fear-impulsed reflexive conditioning that results from being born utterly helpless. Intellectual information-accumulating processing and anticipatory faculties are necessary, and are only slowly discovered as exclusively able to overcome the ignorantly feared frustrating experiences of the past. Science must be seen as a tool of fundamental advantage for all, which Universe requires that man understand and use exclusively for the positive advantage of all of humanity, or humanity itself will be discarded by Universe as a viable evolutionary agent.
826.06 It is to this dilemma that we address ourselves; not being interested in palliatives, we backtrack two and a half millennia to the turning of the road where we entered in the hope of regaining the highway of lucid rationality. Using the same Greek tools, but not starting off with a plane or the subsequently substituted blackboard of the pedagogues working indoors and deprived of direct access to the scratchable Earth surface used by the Near Eastern ancients,4 we will now institute scientific exploration in the measurement of physical reality.

(Footnote 4: With the blackboard the pedagogues were able to bring infinity indoors.)
826.10 Otherness Restraints and Elliptical Orbits
826.11 Angular acceleration is radically restrained accumulation of circular momentum; angular deceleration is the local depletion of angular momentum.
826.12 Release from angular acceleration appears to be linear acceleration, but the linearity is only theoretical. Linear acceleration is the release from the restraint of the nearest accelerator to the angularly accelerative or decelerative restraint of the integrated vectorial resultant of all the neighboringly dominant, forever-otherness restraints in Universe. Linear acceleration never occurs, because there is no cosmic exemption of otherness.
826.13 The hammer thrower releases his "hammer's" ball-and-rod assembly from his extended arm's-end grasp, seemingly allowing the hammer to take a tangentially linear trajectory, but Earth's gravitational pull immediately takes over and converts the quasistraight trajectory into an elliptical arc of greater orbiting radius than before. But the arc is one of ever-decreasing radius as the Earth's gravity takes over and the hammer thrower's steel ball seemingly comes to rest on the Earth's surface, which is, however, in reality traveling around the Earth's axis in synchronized consonance with the other huddled together atoms of the Earth's surface. Near the Earth's equator this would be at a circular velocity of approximately 1000 miles an hour, but near the Earth's poles the velocity would be only inches per hour around the Earth's axis. Both Earth, hammer thrower, and thrown hammer are traveling at 60,000 miles an hour around the Sun at a radial restraint distance of approximately 92 million miles, with the galaxies of Universe's other nonsimultaneously generated restraints of all the othernesses' overlappingly effective dominance variations, as produced by degrees of neighboring energy concentrations and dispersions. It is the pulsation of such concentrations and dispersions that brings about the elliptical orbiting.
826.14 This is fundamental complementarity as intuited in Einstein's curved space prior to the scientific establishment of generalized complementarity, which we may now also speak of as the "generalized otherness" of Universe. This is why there can be only curved space. (See Sec. 1009.52.)
826.15 Isaac Newton's first law of motion, "A body persists in a state of rest or in a straight line except as affected by other forces," should now be restated to say, "Any one considered body persists in any one elliptical orbit until that orbit is altered to another elliptical orbit by the ceaselessly varying interpositionings and integrated restraint effects imposed upon the considered body by the ever-transforming generalized cosmic otherness." A body is always responding orbitally to a varying plurality of otherness forces.

830.00 Foldability of Great Circles

831.00 Sheet of Paper as a System
831.01 Our steel dividers have sharp, straightedged legs, each tapering into sharp points. We can call these dividers "scissors." Scissors are dividers of either linear or angular, i.e. circular, differentiation. We can even make our explorations with some superficial accommodation of the Greeks' propensity for using a plane. For instance, we can take a finite piece of paper, remembering (operationally), however, that it has "thickness" and "edges," which are in fact small area faces. If it is a rectilinear sheet of typewriter paper, we recognize that it has four minor faces and two major faces. The major faces we call "this side" and "the other side," but we must go operationally further in our consideration of what the "piece of paper" is. Looking at its edges with a magnifying glass, we find that those surfaces round over rather brokenly, like the shoulders of a hillside leading to a plateau. We find the piece of paper to be fundamentally the same kind of entity as that which we have watched the baker make as he concocts, stirs, and thickens his piecrust dough, which, after powdering with flour, can be formed into a spherical mass and set upon a flour-powdered surface to be progressively rolled into a thick sheet that may be cut into separate increments of the same approximate dimensions as the "sheet" of typewriter paper.
831.10 Moebius Strip
831.11 In the same operational piecrust-making strictness of observation, we realize that the phase of topology that Moebius employed in developing his famous strip mistakenly assumed that the strip of paper had two completely nonconnected faces of such thinness as to have no edge dimension whatsoever. When we study the Moebius strip of paper and the method of twisting one of its ends before fastening them together and scribing and cutting the central line of the strip only to find that it is still a single circle of twice the circumference and half the width of the strip, we realize that the strip was just a partially flattened section of our piecrust, which the baker would have produced by making a long hard roll, thinner than a breadstick and flattened out with his wooden roller. What Moebius really did was to take a flattened tube, twist one of its ends 180 degrees, and rejoin the tube ends to one another. The scribed line of cutting would simply be a spiral around the tube, which made it clear that the two alternate ends of the spirals were joined to one another before the knifing commenced.
831.20 Cutting Out Circular Cookies
831.21 We can use the leverage of the sheet length of flatness of the paper against the fulcrum of the sheet of paper's thinness to fold it as a relatively flat system, even as the baker could fold over the unbaked piecrust. Or we can scribe upon the paper with our geometrical tools in an approximately accurate measuring manner. What we have done is to flatten our system in a measurefully knowing manner. For operational accommodation, but always by construction, we can for the moment consider the paper's surface as did the Greeks their infinitely extending plane, but we are aware and will always be responsible for "the rest of the system" with which we are working, though we are momentarily preoccupied with only a very local area of the whole.
831.22 We can scribe a circle around the pivotal A-end of the dividers, and we can do so in an approximate "plane." We can strike or scribe the approximately straight diameter through the circle's center. We can now use our divider-scissors to divide the finite circle of paper from the finite balance of the paper system lying outside the circle__that is, we can scissor or "cut" out the area contained by the circle from the balance of the paper, as the baker cuts out circular, wafer-thin cookies. We are at all times dividing reality multidimensionally, no matter how relatively diminutive some of its dimensions may be.
831.23 Because we are dealing with multidimensional reality, we must note operationally that in cutting out our circular piece of paper, we are also cutting our original piece of typewriter paper into two pieces, the other piece of which has a circular hole in its overall rectilinear area. We must keep ourselves conscious of this complementary consequence even though we are for the moment interested only in the cut-out circular piece pricked with the original center of the divider-generated circumference. (The Maori, whose prime love was the Pacific Ocean, looked upon islands as holes in their ocean and upon what man calls harbors or bays as protrusions of the ocean inserted into the land.) Now, from our cut-out circle and our inventory of construction produced information, we learn experimentally that we can lift any point of the perimeter of the circle and fold it over so that the point of the perimeter is congruent with any other point on the perimeter; in doing so, we find that we are always folding the circular system of paper into two semicircles whose hinge lines always run through the points of origin.
831.24 By construction, we can demonstrate that the circle of paper may be folded along its constructionally scribed diameter, and because all of its perimeter points are equidistant from the center of the circle, the semicircular edges are everywhere congruent. We find that we can fold the circle along any of its infinite number of diameters and the two half-circle circumferences (or perimeters = run arounds = racetracks) will always be congruent as folded together. The same infinity of diameters could be used to fold the paper-circle diameters in the opposite direction on the underside of the original plane.
831.25 Having deliberately colored our original paper's two opposite major sides with two different colors, red and white, we will see that our set of paper-circle folding along its infinity of diameters resulted in red half-circles, while the folding in the opposite direction produced all white half-circles. We also discover that as we fold from flat whole circle to congruence with the other half-circle, among any of the infinity of diameters along which to fold, the circumference of any one side of the circle moves toward the circumference on the other half, and as it travels 180 degrees around its diameter hinges, its perimeter thus describes a hemisphere of points all equidistant from the same center of all the hinges.
831.26 Having worked from a unitary plane and employing the infinity of diameters to fold in opposite directions, we discover that all the combined red and white opposite semicircular foldings altogether have produced a sphere consisting of two complementary hemispheres, one red and one white, which altogether represent all the rotatings of the equidistant circumferences, always from the same common center of all the diameters, which fact we know by construction of the diameters by our straightedge along which we scribed through the original center mark of our generation of the circle.
831.30 Six Cases of Foldability of Great Circles

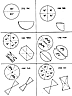Fig. 831.31 		831.31 There are six cases of folding employed in the proof of sixthing of the circle__or hexagoning the circle. (See Illus 831.31.) Case 1 is a limit case with congruence of all diameters.
Next Section: 835.00
Copyright © 1997 Estate of R. Buckminster Fuller