835.00 Bow-Tie Construction of Spherical Octahedron

835.01 With one of the sharp points (A) of dividers (AB) fixed at a point (X) on a flat sheet of paper, sharp point B is rotated cuttingly around until an equiradius circle of paper is cut out. It is discovered experimentally that if any point on the circular perimeter is folded over to any other point on the circle's perimeter, that the circle of paper always folds in such a manner that one-half of its perimeter__and one-half of its area__is always congruent with the other half; and that the folded edge always runs through the exact center point X of the circle and constitutes a diameter line of the circle. This demonstrates that a diameter line always divides both the whole circular area and the circle's perimeter- circumference into two equal halves. If one diameter's end comer W of the circle, folded into halves, is folded over once more to congruence with the corner W' at the other end of the diameter, once again it will be constructively proved that all of the circle's perimeter is congruent with itself in four folded-together layers, which operational constructing also divides the whole circle into four equal parts, with the second folded diameter Y-Y' perpendicular to the first diameter, ergo producing four right-angled comers at the center of the circle as marked by the two diameter fold lines, W-W' and Y-Y'. If we now open the paper circle and turn it over to its reverse side, we fold in a third diameter line T-T' by making circumference point W congruent with circumference point Y (which inadvertently makes point W' congruent with Y'), we will find that we have exactly halved the right angles WXY and W'XY', so that the perimeter distances WT or TY are each exactly half the perimeter distance WY, and either W'T' or T'Y' are each one-half the perimeter distances of either WY, YW', W'Y', or Y'W.

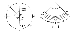Fig. 835.02

835.02 If we now turn the paper circle over once more we find that the spring in the fold lines of the paper will make point T and T' approach each other so that the whole circle once again may be folded flat to produce four congruent surfaces of the paper folded into an overall composite quarter circle with the two quarter-circle outer layers, and four one-eighth circle's two inner layers coming to congruent fold-around terminal tangency at the midpoint and center of the folded, right-angle, quarter-circle packet, with W congruent with Y and W' congruent with Y' and T congruent with T'. Thus it is proven that with three diameter foldlines the whole circle can be subdividingly folded into six arc- and-central-angle increments, ergo also unfoldable again into whole-circle flatness. (See Illus. 835.02.)

835.03 We know that every point on the perimeter of the folded semicircle is equidistant from the point of origin. We may now go to one end of the folded-edge diameter and fold the paper in such a manner that two ends of the diameter are congruent. This will fold the paper circle into four quadrants which, by construction congruence, are exactly equal. The legs of the 90 degree angle formed around the origin of the circle by this second folding are the same in length, being the same radius as that of the circle, ergo, of the halved diameter produced by the second folding. The angle edges and the radii are identical. When we open the quarter-circle of four faces folded together into the semicircle, we find that the second fold edge, which produced the 90-degree angle, is the radius of the diameter perpendicular to the first diameter folded upon. The points where this perpendicular diameter's ends intersect the circumference of the circle are equidistant, by construction, from the diameter ends of the first folded-edge diameter of the semicircle. This folded semicircle, with its secondary fold-mark of verticality to its origin, can be partially folded again on that perpendicular radius so that the partially folded semicircle and its partially folded, vertically impinging fold-line constitute an angularly winged unit, with appearance similar to the outer hard covers of a partially opened book standing bottomless with the book's hard covers vertically perpendicular to a table. This flying- winged, vertically hinged pair of double-thickness quarter-circles will be found to be vertically stable when stood upon a table, that is, allowed to be pulled vertically against the table by gravity. In structural effect, this winged quarter-pair of open, standing "book covers" is a tripod because the two diameter ends, A and B, and the circle's origin point, C, at the middle represent three points, A, B, C, in triangular array touching the table, which act as a triangle base for the tripod whose apex is at the perimeter, T, of the semicircle at the top terminal of the vertical fold. The tripod's legs are uneven, one being the vertical radius of the original circle, TC, and the other two being the equidistance chords, a and b, running from the top of the vertical "book" column's back and leading directly to the two wing terminals, A and B, of the first folded diameter of the original circle. The weight of the paper on either side of the vertical fold extended on only one side of any line produces weight or gravitational effect to keep the vertical edge vertical, not allowing it to lean farther in the direction of the legs due to the relative structural rigidity of the paper itself.

835.04 We will now take five additional pieces of paper, making six in all, producing the circles on each of the same radius with our dividers welded and using the scissor function of the dividers' cuttingly ground straightedges. We cut the circles out and fold them in the manner already described to produce the vertically standing, angular interaction of the four quadrants of paper, standing as a vertically edged tripod with double thicknesses of the paper in arced flanges acting as legs to stabilize their verticality. We now have six such assemblies. We can take any two of them that are standing vertically and bring the vertical edges of their tripods together. (We know that they are the same size and that the vertical hinges are dimensionally congruent because they are all of the same radius length produced by the dividers.) We move two of their vertically folded edges into tangential congruence, i.e., back-to-back. The vertical perimeter terminals of their vertically folded hinges and their circle-center origins at the bottom of the hinges are congruent.

835.05 To hold their vertical hinges together and to free our hands for other work, we slip a bobby pin over their four thicknesses of paper, holding their two angles together in the pattern of a cross as viewed vertically from above or below. This construction produces a quadripod. Now I can grasp this cross between two of my fingers inserted into the angles of the cross and lift it from the table, turning it upside down in my hands and finding the other side of the cross, all four lines of which are in the same (approximately flat) plane, in contradistinction to the way the cross looked when those four folded edges sat on the table and had four arcing lines running in four different directions from their vertical congruence. I will insert a bobby pin to hold together the cross at its folded-line intersection. With its flat cross down, it will now stand as the partial profiling of a hemisphere. When I put the arced cross down on the table, it will roll around as would half a wooden ball. Placing it on the table in this roll-around hemisphere attitude, I can stabilize it with underprops so that the plane of four folded edges coming together on top will be approximately horizontal and parallel to the table top.

835.06 I may now take one of the four additional quadri-folded, partially opened, hinged, quarter-circle, double-thickness assemblies first described as able to stand vertically by themselves. Each of the four can be made to stand independently with one of its 90-degree, quarter-circle wings lying horizontally on the table and its other quarter-fold wing standing approximately vertically. The four quarter-circles on the table can be slid together to form a whole circle base; bobby pins can be inserted at their four circumference terminals to lock them together in a circle; and their four approximately vertical flanges can be hinged into true verticality so that they form two half-circle arcs, passing through one another perpendicularly to one another. They will have a common vertical radius (by construction) at the common top terminal, and all of their four vertical hinges' two crossing bobby pins can be inserted to lock this vertex together. This assembly of four of the six units with circular base can now be superimposed upon the first pair of hinges sitting on the table with hemisphere down and its planar cross up. The four cross ends of that first assembly can be hinged around into congruence with the 90-degree circumference points of the top assembled four units, with everything firmly congruent by construction.

835.07 We will now take bobby pins and fasten the folded flanking edge ends of the top-four assembly congruent with each of the four edges of the hemispherical cross group on the table.

835.08 Fastened by bobby pins at the congruent perimeter terminals of the folded cross lines, this top assembly stabilizes the previously unstable angular space between any two of the cross-forming hemispherical groups prop-stabilized, bowl down, with the plane of its four-way hinge cross horizontal and parallel to the table. The angle between any two of the horizontally crossed assembly members is now stabilized at exactly one-quarter of a circle by the integrity of construction procedures of our experiment. This produces one complete horizontal circle with 90-degree triangular webbing of double-folded paper perpendicular to two other perpendicularly intersecting vertical circles, each of which also consist of four 90-degree triangular webs of double-thickness paper, each of all 12 of which 90-degree triangular webs structurally stabilizes the six radial hinges of the three XYZ axes of this spherically profiled system assembly, prop-stabilized not to roll on the table.

835.09 In effect, we have the original six circular pieces reassembled with one another as two sets of three circles symmetrically intercepting one another. We know that each of the six quadrantly folded units fit into the remaining angular spaces because, by construction, each of the angles was folded into exactly one-quarter of a circle and folded together exactly to complete their circle. And we know that all the radial hinges fit together because they are constructionally of equal length. We have now a triangularly stabilized structure constituting what is called the spherical octahedron. Its vertical axis has polar terminals we call north and south. South is congruent with the table, and north is at the apex of the assembly. It has four equatorial points lying in a plane horizontal to the table. It is called the spherical octahedron because it has an external pattern subdivided exactly, evenly, and symmetrically by eight spherical triangles, four in the northern hemisphere and four in the southern hemisphere.

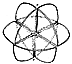Fig. 835.10

835.10 We find that the construction has three distinct planes that are all symmetrical and perpendicular to one another; the horizontal equatorial plane and two vertical planes intersect each other on the north-south polar axis perpendicularly to one another, which perpendicularity is constructurally inherent. Each of the perpendicularly intersecting great circles is seen to be of a double thickness due to the folding of the six original paper great circles, which now appear, deceptively, as three, but are not continuous planes, being folded to make their hinges congruent. (See Illus. 835.10.)

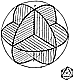Fig. 835.11

835.11 The spherical octahedron provides the basis for the frame of reference of the constructionally proven verticality of its axis in respect to its equatorial plane and the equidistance of the poles from all the perimeter points. (See Illus. 835.11.)

835.12 As we rotate this octahedron rapidly on any one of its three axes, the rotated perimeters generate optically what can be called a dynamically generated true sphere. By construction, every point on the sphere's dynamically high-frequency event-occurring is equidistant from the central origin__our initial scribing position of one end of the dividers whose central angle we locked by welding it into unalterability.

836.00 Spherical Octahedron: Alternate Assembly

836.01 In addition to the foregoing operational development of the octahedron, we discover that the assembling of the spherical octahedron called for a fundamental asymmetry of procedure. That is, we assemble two of its quadrantly folded great circles to form one hemisphere and four of the quadrantly folded great circles to form the other hemisphere. In this method, the equator has to be included in either the northern or the southern hemisphere.

836.02 Therefore, in attempting to find some other method of assembly, we find that the spherical octahedron can be alternatively assembled in three sets of two quadrantly folded great circles. This is done by following all of the general procedures for developing the six quadrantly folded circles and their stand-up-ability as open book backs, producing a tripoding stability with the angle hinged by the variability of the vertical book-back spine.

836.03 We will now make three pairs of these variantly angled, quadrantly folded circles. We find that instead of standing one of them as a book with its hinge-spine vertical, the book can be laid with one of its faces parallel to the table and the other pointing approximately vertically, outward from the table. Due to the relative inflexibility of the double-folded angle of the greatcircle construction paper, the book can be laid on its front face or its back face. We will take two of them sitting on the front face of the book with their backs reaching outwardly, vertically away from the table. We move two in front of us, one right and one left. We will rotate the right-hand one counterclockwise, 90 degrees around its vertical axis. Then we move the quadrant angle of the right-hand one into congruence with the quadrant angle of the left-hand one. We stabilize the variable angle of the right-hand one between its vertical and horizontal parts by fastening with two bobby pins the constructionally produced stable quadrant of the folded parts of the right- hand unit. This gives us a constructionally proven one-eighth of a sphere in an asymmetrical assembly, having the 1 80-degree axis of the sphere lying congruent with the table. On one end of the axis, we have the stabilized quadrant angle; on the other end of the axis, we have the open, unstabilized angle.

836.04 With the other four of our six quadrantly folded circles, we make two more paired assemblies in exactly the same manner as that prescribed for the first paired assembly. We now have three of these assemblies with their axes lying on the table; on the left-hand side of all three, there will be found the stabilized, spherical-octant triangle. On the left side, there is a folded quadrant, where the angle between the vertical axis of the spherical octant is approximately 90 degrees from the folded axis lying on the table__but an unstabilized 90 degrees; it can be stabilized into 90-degreeness by virtue of the fact that both of its open folded edges are radii of the sphere by construction and have an accommodating, open hinge-line. We notice then that the three axes lying on the table, as the interior edge of the semicircle of double-ply folded paper, represent the three XYZ axes of the octahedron as well as the XYZ 90-degree coordinates of the international scientific standards of comprehensive mensuration__as, for instance, the X axis represents the height, Y the width, and Z the breadth. Geographically, this would represent the north and south poles and the four perpendicular quadrants of the equator.

836.05 Our operational-construction method employs the constant radius and identifies every point on the circumference and every point on the internal radii. This is in contradistinction to analytic geometry, in which the identification is only in terms of the XYZ coordinates and the perpendiculars to them. Analytic geometry disregards circumferential construction, ergo, is unable to provide for direct identification of angular accelerations.

836.06 These three subassemblies of the six folded quadrants are inherently asymmetrical. It was the fundamental asymmetry that made it possible to make the spherical octahedron with only three whole circles of paper, but we found it could only be accomplished symmetrically with six quadrantly folded great circles, with the symmetry being provided by the duality, by the twoness.

836.07 All three assemblies are identically asymmetric. The loaded XYZ axes hold the Y axis vertically. Pick up the Y axis and turn it 90 degrees to the X axis. This brings one of the stabilized quadrants of the Y axis into congruence with one of the nonstabilized quadrants of the X axis__to stabilize it. With the Y axis now at 90 degrees to the X axis, we can fasten the two assemblies into place with bobby pins.

836.08 Take the Z axis assembly and hold it so that it is perpendicular to both the X and Y axes; this will bring the three constructionally proven folded quadrangles into congruence with the three folded, as yet unstabilized, 90-degree sinuses of the X and Y axis assemblies.