 Foldability of Four Great Circles of Vector Equilibrium
Foldability of Four Great Circles of Vector Equilibrium
840.00  Foldability of Four Great Circles of Vector Equilibrium
Foldability of Four Great Circles of Vector Equilibrium

|
841.00
 Foldability Sequence
Foldability Sequence
|

|
841.11
 Using the method of establishing perpendiculars produced
by the
overlapping of unit-radius circles in the first instance
of the Greeks' exclusively one-planar
initiation of their geometry (see Illus.
455.11), a
diameter PP' perpendicular to the first
straightedge constructed diameter DD' can be constructed.
If we now fold the paper
circles around DD' and PP', it will be found that every
time the circles are folded, the
points where the perpendicular to that diameter intercept
the perimeter are inherently
congruent with the same perpendicular's diametrically
opposite end.
Using the method of establishing perpendiculars produced
by the
overlapping of unit-radius circles in the first instance
of the Greeks' exclusively one-planar
initiation of their geometry (see Illus.
455.11), a
diameter PP' perpendicular to the first
straightedge constructed diameter DD' can be constructed.
If we now fold the paper
circles around DD' and PP', it will be found that every
time the circles are folded, the
points where the perpendicular to that diameter intercept
the perimeter are inherently
congruent with the same perpendicular's diametrically
opposite end.
|

|
841.12
 The succession of positive and negative foldings in
respect to the original
plane folded around a plurality of diameters of that
plane will define a sphere with inherent
poles P and P', which occur at the point of crossing
of the rotated perpendiculars to the
folded-upon diameters, the PP' points being commonly
equidistant from the first prime, as
yet unfolded circle cut out from the first piece of
paper. This constructional development
gives us a sphere with a polar axis PP' perpendicular
to the original plane's circle at the
center of that circle. We can also fold six great circles
of unit radius, first into half-circle,
180-degree-arc units, and then halve-fold those six
into 90-degree "bookends," and
assemble them into a spherical octahedron with three
axes, and we can rotate the
octahedron around axis PP' and thus generate a spherical
surface of uniform radii.
The succession of positive and negative foldings in
respect to the original
plane folded around a plurality of diameters of that
plane will define a sphere with inherent
poles P and P', which occur at the point of crossing
of the rotated perpendiculars to the
folded-upon diameters, the PP' points being commonly
equidistant from the first prime, as
yet unfolded circle cut out from the first piece of
paper. This constructional development
gives us a sphere with a polar axis PP' perpendicular
to the original plane's circle at the
center of that circle. We can also fold six great circles
of unit radius, first into half-circle,
180-degree-arc units, and then halve-fold those six
into 90-degree "bookends," and
assemble them into a spherical octahedron with three
axes, and we can rotate the
octahedron around axis PP' and thus generate a spherical
surface of uniform radii.
|

|
841.13
 We could also have constructed the same sphere by
keeping point A of the
dividers at one locus in Universe and swinging point
B in a multiplicity of directions
around A (see Illus.
841.15
). We now know that every
point on the surface of an
approximate sphere is equidistant from the same center.
We can now move point A of the
dividers from the center of the constructed sphere to
any point on the surface of the
sphere, but preferably to point P perpendicular to an
equatorially described plane as in
We could also have constructed the same sphere by
keeping point A of the
dividers at one locus in Universe and swinging point
B in a multiplicity of directions
around A (see Illus.
841.15
). We now know that every
point on the surface of an
approximate sphere is equidistant from the same center.
We can now move point A of the
dividers from the center of the constructed sphere to
any point on the surface of the
sphere, but preferably to point P perpendicular to an
equatorially described plane as in
|

|
841.11 and 841.12 . And we can swing the free point B to strike a circle on the surface of the sphere around point P. Every point in the spherical surface circle scribed by B is equidistant chordally from A, which is pivotally located at P, that is, as an apparently straight line from A passing into and through the inside of the spherical surface to emerge again exactly in the surface circle struck by B, which unitary chordal distance is, by construction, the same length as the radius of the sphere, for the opening of our divider's ends with which we constructed the sphere was the same when striking the surface circle around surface point A. |

|
841.14
 We now select any point on the spherical surface circle
scribed by point B of
the dividers welded at its original radius-generating
distance with which we are conducting
all our exploration of the spheres and circles of this
operational geometry. With point A of
the dividers at the north-polar apex, P', of the spherical
octahedron's surface, which was
generated by rotating the symmetrical assembly of six
90-degree, quadrangularly folded
paper circles. Axis PP' is one of its three rectilinearly
interacting axes as already
constructively described.
We now select any point on the spherical surface circle
scribed by point B of
the dividers welded at its original radius-generating
distance with which we are conducting
all our exploration of the spheres and circles of this
operational geometry. With point A of
the dividers at the north-polar apex, P', of the spherical
octahedron's surface, which was
generated by rotating the symmetrical assembly of six
90-degree, quadrangularly folded
paper circles. Axis PP' is one of its three rectilinearly
interacting axes as already
constructively described.
|
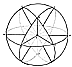 Fig. 841.15A 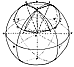 Fig. 841.15B |
841.15
 We now take any point, J, on the spherical surface
circle scribed by the
divider's point B around its rotated point at P. We
now know that K is equidistant
chordally from P and from the center of the sphere.
With point A of our dividers on J, we
strike point K on the same surface circle as J, which
makes J equidistant from K, P, and X,
the center of the sphere. Now we know by construction
integrity that the spherical radii
XJ, XK, and XP are the same length as one another and
as the spherical chords PK, JK,
and JP. These six equilength lines interlink the four
points X, P, J, and K to form the
regular equiedged tetrahedron. We now take our straightedge
and run it chordally from
point J to another point on the same surface circle
on which JK and K are situated, but
diametrically opposite K. This diametric positioning
is attained by having the chord-
describing straightedge run inwardly of the sphere and
pass through the axis PP',
emerging from the sphere at the surface-greatcircle
point R. With point A of the dividers
on point R of the surface circle__on which also lies
diametrically point K__we swing point
B of the dividers to strike point S also on the same
spherical surface circle around P, on
which now lie also the points J, K and R, with points
diametrically opposite J, as is known
by construction derived information. Points R, S, P,
and X now describe another regular
tetrahedron equiedged with tetrahedron JKPX; there is
one common edge, PX, of both
tetrahedra. PX is the radius of the spherical, octahedrally
constructed sphere on whose
surface the circle was struck around one of its three
perpendicularly intersectioned axes,
and the three planes through them intersect congruently
with the three axes by
construction. PX is perpendicular to the equatorial
plane passing through W, Y, W', Y' of
the spherical octahedron's three axes PP', WW', and
YY'.
We now take any point, J, on the spherical surface
circle scribed by the
divider's point B around its rotated point at P. We
now know that K is equidistant
chordally from P and from the center of the sphere.
With point A of our dividers on J, we
strike point K on the same surface circle as J, which
makes J equidistant from K, P, and X,
the center of the sphere. Now we know by construction
integrity that the spherical radii
XJ, XK, and XP are the same length as one another and
as the spherical chords PK, JK,
and JP. These six equilength lines interlink the four
points X, P, J, and K to form the
regular equiedged tetrahedron. We now take our straightedge
and run it chordally from
point J to another point on the same surface circle
on which JK and K are situated, but
diametrically opposite K. This diametric positioning
is attained by having the chord-
describing straightedge run inwardly of the sphere and
pass through the axis PP',
emerging from the sphere at the surface-greatcircle
point R. With point A of the dividers
on point R of the surface circle__on which also lies
diametrically point K__we swing point
B of the dividers to strike point S also on the same
spherical surface circle around P, on
which now lie also the points J, K and R, with points
diametrically opposite J, as is known
by construction derived information. Points R, S, P,
and X now describe another regular
tetrahedron equiedged with tetrahedron JKPX; there is
one common edge, PX, of both
tetrahedra. PX is the radius of the spherical, octahedrally
constructed sphere on whose
surface the circle was struck around one of its three
perpendicularly intersectioned axes,
and the three planes through them intersect congruently
with the three axes by
construction. PX is perpendicular to the equatorial
plane passing through W, Y, W', Y' of
the spherical octahedron's three axes PP', WW', and
YY'.
|

|
841.16
 We may now take the congruent radius edge PX of the
two tetrahedra and
separate it into the two radii (PX)1 and (PX)2 and rotate
their two P ends (PM) and (PN),
away from one another around the sphere's center, X,
until (PM) and (PX) are
diametrically opposite one another. Therefore, points
(PM) and (PN) are now lying in the
octahedron's equatorial plane WXW'Y'. We may now rotate
points J, K, R, and S around
the (PM), X (PN) axis until points J, K, R, and S all
lie in the octahedral plane WY W'X',
which converts the opened unitary construction first
into a semifolded circle and then into
a circle congruent with the octahedron's equatorial
plane, all of which six-hinged
transformation was permitted as all the seven points__(PM),
J, K, (PN), S, R, X__were at
all times equidistant from one another, with no restraints
placed on the motion. We now
have the hexagonally divided circle as a constructionally
proven geometrical relationship;
and therefore we have what the Greeks could not acquire:
i.e., a trisected 180-degree
angle; ergo a six-equiangular subdivision of spherical
unity's 360 degrees into 60-degree
omniequiangularity; ergo a geometrically proven isotropic
vector matrix operational
evolvement field.
We may now take the congruent radius edge PX of the
two tetrahedra and
separate it into the two radii (PX)1 and (PX)2 and rotate
their two P ends (PM) and (PN),
away from one another around the sphere's center, X,
until (PM) and (PX) are
diametrically opposite one another. Therefore, points
(PM) and (PN) are now lying in the
octahedron's equatorial plane WXW'Y'. We may now rotate
points J, K, R, and S around
the (PM), X (PN) axis until points J, K, R, and S all
lie in the octahedral plane WY W'X',
which converts the opened unitary construction first
into a semifolded circle and then into
a circle congruent with the octahedron's equatorial
plane, all of which six-hinged
transformation was permitted as all the seven points__(PM),
J, K, (PN), S, R, X__were at
all times equidistant from one another, with no restraints
placed on the motion. We now
have the hexagonally divided circle as a constructionally
proven geometrical relationship;
and therefore we have what the Greeks could not acquire:
i.e., a trisected 180-degree
angle; ergo a six-equiangular subdivision of spherical
unity's 360 degrees into 60-degree
omniequiangularity; ergo a geometrically proven isotropic
vector matrix operational
evolvement field.
|

|
841.17
 With our operationally considerate four tools of divider,
straightedge and
scriber and measurably manipulable scribable system
as a material object (in this case, a
sheet of paper; later, four sheets of paper), and with
our constructionally proven
symmetrical subdivision of a circle into six equilateral
triangles and their six chord-
enclosed segments, we now know that all the angles of
the six equilateral triangles around
center X are of 60 degrees; ergo, the six triangles
are also equiangular. We know that the
six circumferential chords are equal in length to the
six radii. This makes it possible to
equate rationally angular and linear accelerations,
using the unit-radius chord length as
the energy-vector module of all physical-energy accelerations.
We know that any one of
the 12 lines of the equilaterally triangled circle are
always either in 180-degree extension
of, or are parallel to, three other lines. We may now
take four of these hexagonally divided
circles of paper. All four circular pieces of paper
are colored differently and have different
colors on their opposite faces; wherefore, there are
eight circular faces in eight colors
paired in opposite faces, e.g., red and orange, yellow
and green, blue and violet, black and
white.
With our operationally considerate four tools of divider,
straightedge and
scriber and measurably manipulable scribable system
as a material object (in this case, a
sheet of paper; later, four sheets of paper), and with
our constructionally proven
symmetrical subdivision of a circle into six equilateral
triangles and their six chord-
enclosed segments, we now know that all the angles of
the six equilateral triangles around
center X are of 60 degrees; ergo, the six triangles
are also equiangular. We know that the
six circumferential chords are equal in length to the
six radii. This makes it possible to
equate rationally angular and linear accelerations,
using the unit-radius chord length as
the energy-vector module of all physical-energy accelerations.
We know that any one of
the 12 lines of the equilaterally triangled circle are
always either in 180-degree extension
of, or are parallel to, three other lines. We may now
take four of these hexagonally divided
circles of paper. All four circular pieces of paper
are colored differently and have different
colors on their opposite faces; wherefore, there are
eight circular faces in eight colors
paired in opposite faces, e.g., red and orange, yellow
and green, blue and violet, black and
white.
|

|
841.18
 We will now take the red-orange opposite-faced construction-paper
circle.
We fold it first on its (PM)-(PN) axis so that the red
is hidden inside and we see only an
orange half-circle's two-ply surface. We next unfold
it again, leaving the first fold as a
crease. Next we fold the circle on its RX axis so that
the orange face is inside and the red
is outside the two-ply, half-circled foldup. We unfold
again, leaving two crossing, axially
folded creases in the paper. We next fold the same paper
circle once more, this time along
its JS axis in such a manner that the orange is inside
and once again only the red surface is
visible, which is the two-ply, half-circle folded condition.
We will now take the red-orange opposite-faced construction-paper
circle.
We fold it first on its (PM)-(PN) axis so that the red
is hidden inside and we see only an
orange half-circle's two-ply surface. We next unfold
it again, leaving the first fold as a
crease. Next we fold the circle on its RX axis so that
the orange face is inside and the red
is outside the two-ply, half-circled foldup. We unfold
again, leaving two crossing, axially
folded creases in the paper. We next fold the same paper
circle once more, this time along
its JS axis in such a manner that the orange is inside
and once again only the red surface is
visible, which is the two-ply, half-circle folded condition.
|

|
841.19
 We now unfold the red-orange opposite-faced colored-paper
circle, leaving
two positive and one negative creases in it. We will
find that the circle of paper is now
inclined by its creases to take the shape of a double
tetrahedron bow tie, as seen from its
openings end with the orange on the inside and the red
on the outside. We may now insert
a bobby pin between points (PM) and (PN), converting
this hexagonally subdivided and
positively__negatively folded circle back into the mutually
congruent PX edge, two
(hinge-bonded, bivalent) tetrahedra: JKPX and RSPX.
We now unfold the red-orange opposite-faced colored-paper
circle, leaving
two positive and one negative creases in it. We will
find that the circle of paper is now
inclined by its creases to take the shape of a double
tetrahedron bow tie, as seen from its
openings end with the orange on the inside and the red
on the outside. We may now insert
a bobby pin between points (PM) and (PN), converting
this hexagonally subdivided and
positively__negatively folded circle back into the mutually
congruent PX edge, two
(hinge-bonded, bivalent) tetrahedra: JKPX and RSPX.
|

|
841.20
 We may now fold the other three circles into similar,
edge-bonded,
tetrahedral bow-tie constructions in such a manner that
number two is yellow outside and
green inside; number three of the 60-degree-folded bow
ties is blue outside and violet
inside; and the fourth bow tie, identical to the other
three bow ties' geometrical aspects of
60-degree equiangularity and equiradius chord edges,
is black outside and white inside.
We may now fold the other three circles into similar,
edge-bonded,
tetrahedral bow-tie constructions in such a manner that
number two is yellow outside and
green inside; number three of the 60-degree-folded bow
ties is blue outside and violet
inside; and the fourth bow tie, identical to the other
three bow ties' geometrical aspects of
60-degree equiangularity and equiradius chord edges,
is black outside and white inside.
|

|
841.21
 We may take any two of these bow ties__say, the orange
inside and the
green inside__and fasten each of their outside corners
with bobby pins, all of their radii
being equal and their hinges accommodating the interlinkage.
We may take any two of these bow ties__say, the orange
inside and the
green inside__and fasten each of their outside corners
with bobby pins, all of their radii
being equal and their hinges accommodating the interlinkage.
|
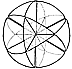 Fig. 841.22 |
841.22
 Each of these paired bow-tie assemblies, the orange-green
insiders and the
violet-white insiders, may now be fastened bottom-to-bottom
to each other at the four
external fold ends of the fold cross on their bottoms,
with those radial crosses inherently
congruent. This will reestablish and manifest each of
the four original circles of paper, for
when assembled symmetrically around their common center,
they will be seen to be
constituted of four great circles intersecting each
other through a common center in such a
manner that only two circular planes come together at
any other than their common center
point and in such a manner that each great circle is
divided entirely into six equilateral
triangular areas, with all of the 12 radii of the system
equilengthed to the 24
circumferential chords of the assembly. Inasmuch as
each of the 12 radii is shared by two
great circle planes, but their 24 external chords are
independent of the others, the seeming
loss of 12 radii of the original 24 is accounted for
by the 12 sets of congruent pairs of radii
of the respective four hexagonally subdivided great
circles. This omniequal line and angle
assembly, which is called the vector equilibrium, and
its radii-chord vectors accommodate
rationally and simultaneously all the angular and linear
acceleration forces of physical
Universe experiences.
Each of these paired bow-tie assemblies, the orange-green
insiders and the
violet-white insiders, may now be fastened bottom-to-bottom
to each other at the four
external fold ends of the fold cross on their bottoms,
with those radial crosses inherently
congruent. This will reestablish and manifest each of
the four original circles of paper, for
when assembled symmetrically around their common center,
they will be seen to be
constituted of four great circles intersecting each
other through a common center in such a
manner that only two circular planes come together at
any other than their common center
point and in such a manner that each great circle is
divided entirely into six equilateral
triangular areas, with all of the 12 radii of the system
equilengthed to the 24
circumferential chords of the assembly. Inasmuch as
each of the 12 radii is shared by two
great circle planes, but their 24 external chords are
independent of the others, the seeming
loss of 12 radii of the original 24 is accounted for
by the 12 sets of congruent pairs of radii
of the respective four hexagonally subdivided great
circles. This omniequal line and angle
assembly, which is called the vector equilibrium, and
its radii-chord vectors accommodate
rationally and simultaneously all the angular and linear
acceleration forces of physical
Universe experiences.
|
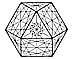 Fig. 841.30 |
841.30
 Trisection by Inherent Axial Spin of Systems
Trisection by Inherent Axial Spin of Systems
|

|
841.31
 The 12 great circles of the vector equilibrium's hemispherical
self-halvings
inherently__and
inadvertently__centrally trisect each
of the vector equilibrium's eight
equiangle spherical triangles, centrally subdividing
those triangles into twelve 30-degree
angles.
The 12 great circles of the vector equilibrium's hemispherical
self-halvings
inherently__and
inadvertently__centrally trisect each
of the vector equilibrium's eight
equiangle spherical triangles, centrally subdividing
those triangles into twelve 30-degree
angles.
|

|
842.00
 Generation of Bow Ties
Generation of Bow Ties
|

|
842.01
 When we consider the "jitterbug" vector equilibrium
contracting into the
icosahedron, bearing in mind that it is all double-bonded,
we discover that, when the
jitterbug gets to the octahedron phase, there really
are two octahedra there.... Just as when
you get three great circles, each one is doubled so
that there are really six.... In making my
tests, taking whole great circles of paper, doing my
spherical trigonometry, learning the
central angles, making those bow ties as a complex,
which really amounts to tetrahedra
bonded edge-to-edge with a common center, they link
up as a chain and finally come
together to make the icosahedron in a very asymmetrical
manner. The 10, 12, and 15 great
circles re-establish themselves, and every one of them
can be folded.
When we consider the "jitterbug" vector equilibrium
contracting into the
icosahedron, bearing in mind that it is all double-bonded,
we discover that, when the
jitterbug gets to the octahedron phase, there really
are two octahedra there.... Just as when
you get three great circles, each one is doubled so
that there are really six.... In making my
tests, taking whole great circles of paper, doing my
spherical trigonometry, learning the
central angles, making those bow ties as a complex,
which really amounts to tetrahedra
bonded edge-to-edge with a common center, they link
up as a chain and finally come
together to make the icosahedron in a very asymmetrical
manner. The 10, 12, and 15 great
circles re-establish themselves, and every one of them
can be folded.
|

|
842.02
 You cannot make a spherical octahedron or a spherical
tetrahedron by itself.
You can make a spherical cube with two spherical tetrahedra
in the pattern of the six great
circles of the vector equilibrium. It becomes a symmetrically
triangulated cube. In fact, the
cube is not structurally stabilized until each of its
six unstable, square-based, pyramidal
half-octahedra are subdivided respectively into two
tetrahedra, because one tetrahedron
takes care of only four of the eight vertexes. For a
cube to be triangulated, it has to have
two tetrahedra.
You cannot make a spherical octahedron or a spherical
tetrahedron by itself.
You can make a spherical cube with two spherical tetrahedra
in the pattern of the six great
circles of the vector equilibrium. It becomes a symmetrically
triangulated cube. In fact, the
cube is not structurally stabilized until each of its
six unstable, square-based, pyramidal
half-octahedra are subdivided respectively into two
tetrahedra, because one tetrahedron
takes care of only four of the eight vertexes. For a
cube to be triangulated, it has to have
two tetrahedra.
|

|
842.03
 There is no way to make a single spherical tetrahedron:
its 109° 28' of angle
cannot be broken up into 360-degree-totaling spherical
increments. The tetrahedron, like
the octahedron, can be done only with two tetrahedra
in conjunction with the spherical
cube in the pattern of the six great circles of the
vector equilibrium.
There is no way to make a single spherical tetrahedron:
its 109° 28' of angle
cannot be broken up into 360-degree-totaling spherical
increments. The tetrahedron, like
the octahedron, can be done only with two tetrahedra
in conjunction with the spherical
cube in the pattern of the six great circles of the
vector equilibrium.
|

|
842.04
 Nor can we project the spherical octahedron by folding
three whole great
circles. The only way you can make the spherical octahedron
is by making the six great
circles with all the edges double__exactly as you have
them in the vector equilibrium__as
a strutted edge and then it contracts and becomes the
octahedron.
Nor can we project the spherical octahedron by folding
three whole great
circles. The only way you can make the spherical octahedron
is by making the six great
circles with all the edges double__exactly as you have
them in the vector equilibrium__as
a strutted edge and then it contracts and becomes the
octahedron.
|

|
842.05
 There is a basic cosmic sixness of the two sets of
tetrahedra in the vector
equilibrium. There is a basic cosmic sixness also in
an octahedron minimally-great-circle-
produced of six great circles; you can see only three
because they are doubled up. And
there are also the six great circles occurring in the
icosahedron. All these are foldable of
six great circles which can be made out of foldable
disks.
There is a basic cosmic sixness of the two sets of
tetrahedra in the vector
equilibrium. There is a basic cosmic sixness also in
an octahedron minimally-great-circle-
produced of six great circles; you can see only three
because they are doubled up. And
there are also the six great circles occurring in the
icosahedron. All these are foldable of
six great circles which can be made out of foldable
disks.
|

|
842.06
 This sixness corresponds to our six quanta: our six
vectors that make one
quantum.
This sixness corresponds to our six quanta: our six
vectors that make one
quantum.
|

|
842.07
 There are any number of ways in which the energy can
go into the figure-
eight bow ties or around the great circle. The foldability
reveals holdings patterns of
energy where the energy can go into local circuits or
go through the points of contact.
One light year is six trillion miles, and humans see
Andromeda with naked eye one million light years
away, which means six quintillion miles.
You can reflect philosophically on some of the things
touch does, like making people want to get their
hands on the coin, the key, or whatever it may be.
This is a typical illustration of total energy accounting,
which all society must become conversant with in
short order if we are to pass through the crisis and
flourish upon our planet. If we do succeed, it will
be
because, among other planetary events, humans will have
come to recognize that the common wealth
equating accounting must be one that locks fundamental
and central energy incrementations-such as
kilowatt hours-to human physical-energy work capability
and its augmentation by the mind-
comprehending employability of generalized principles
of Universe, as these may be realistically
appraised in the terms of increasing numbers of days
for increasing numbers of lives we are thus far
technically organized to cope with, while accommodating
increasing hours and distances of increasing
freedoms for increasing numbers of human beings. All
of this fundamental data can be introduced into
world computer memories, which can approximately instantly
enlighten world humanity on its
increasingly more effective options of evolutionary
cooperation and fundamentally spontaneous social
commitment.
There are any number of ways in which the energy can
go into the figure-
eight bow ties or around the great circle. The foldability
reveals holdings patterns of
energy where the energy can go into local circuits or
go through the points of contact.
One light year is six trillion miles, and humans see
Andromeda with naked eye one million light years
away, which means six quintillion miles.
You can reflect philosophically on some of the things
touch does, like making people want to get their
hands on the coin, the key, or whatever it may be.
This is a typical illustration of total energy accounting,
which all society must become conversant with in
short order if we are to pass through the crisis and
flourish upon our planet. If we do succeed, it will
be
because, among other planetary events, humans will have
come to recognize that the common wealth
equating accounting must be one that locks fundamental
and central energy incrementations-such as
kilowatt hours-to human physical-energy work capability
and its augmentation by the mind-
comprehending employability of generalized principles
of Universe, as these may be realistically
appraised in the terms of increasing numbers of days
for increasing numbers of lives we are thus far
technically organized to cope with, while accommodating
increasing hours and distances of increasing
freedoms for increasing numbers of human beings. All
of this fundamental data can be introduced into
world computer memories, which can approximately instantly
enlighten world humanity on its
increasingly more effective options of evolutionary
cooperation and fundamentally spontaneous social
commitment.
|
| Next Chapter: 900.00 |