1100.00 TRIANGULAR GEODESICS

1101.00 Triangular Geodesics Transformational Projection Model

1101.01 Description

Fig. 1101.02

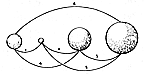
1101.02 The transformational projection is contained entirely within a plurality of great-circle-bounded spherical triangles (or quadrangles or multipolygons) of constant, uniform-edge-module (invariant, central-angle-incremented) subdivisioning whose constantly identical edge length permits their hinging into flat mosaic-tile continuities. The planar phase of the transformation permits a variety of hinged-open, completely flat, reorientable, unit-area, world mosaics. The transformational projection model demonstrates how the mosaic tiles migrate zonally. It demonstrates how each tile transforms cooperatively but individually, internally from compound curvature to flat surface without interborder-crossing deformation of the mapping data.

1102.00 Construction of the Model

1102.01 The empirical procedure modeling that demonstrates the transformational projection is constructed as follows:

1102.02 There are three spring-steel straps of equal length, each of which is pierced with rows of holes located at equal intervals, one from the other, along the longitudinal center line of the straps' flat surfaces; the first and last holes are located inward from the ends a distance equal to one-half the width of the steel straps' flat surfaces.

1102.03 Steel rods of equal length are inserted an equal distance through each of the holes in the straps in such a manner that each rod is perpendicular to the parallel surfaces of the strap and therefore parallel to the other rods. Each of the straps and their respective rods form, in effect, a long-toothed comb, with the comb's straight back consisting of the steel strap.

1102.04 Assuming that the steel straps are flexible, and assuming that each of the rods is absolutely stiff (as when employed as a lever), if the rods have their long lower ends gathered toward one another, at one point the strap will yield by curving of its flat surface to the section of a cylinder whose axis is perpendicular to the plane of the rods and congruent with the rod ends. The strap is bent into an arc of a true circle whose radius is uniformly that of the uniform rod lengths. Each of the rods, as a radius of the circular arc, is perpendicular to the arc. That is, the rods are constantly perpendicular to the strap in either its flat condition or in any of its progressive arcings.

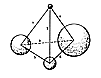
1102.05 Next, one of the two ends of each of the three steel straps is joined to an end of one of the other two straps by means of their end rods being removed and one of the rods being reinserted through their mutual end holes as one strap is superimposed on the other with their respective end holes being brought into register, whereafter, hollow "stovepipe" rivets1 of complementary inside-outside diameters are fastened through the end holes to provide a journal through which one of the former end rods is now perpendicularly inserted, thus journaled pivotally together like a pair of scissors. The three straps joined through their registered terminal holes form an equilateral triangle of overlapping and rotatably journaled ends. (See Illus. 1101.02F.) (Footnote 1: The rivets resemble hollow, tublike grommets.)

1102.06 It will next be seen that a set of steel rods of equal length may be inserted an equal distance through each of the holes of each of the straps, including the hollow journaled holes at the ends, in such a manner that each rod is perpendicular to the parallel surfaces of the straps; therefore, each rod is parallel to the others. All of the rods perpendicularly piercing any one of the straps are in a row, and all of their axes are perpendicular to one common plane. The three unique planes of the three rows of rods are perpendicular to each of the straps whose vertical faces form a triangular prism intersecting one another at the central axes of their three comer rods' common hinge extensions. Each of the three planes is parallel to any one rod in each of the other two planes. (See Illus. 1101.02I.)

1103.00 Flexing of Steel Straps

1103.01 Assuming that each of the rods is absolutely stiff (as when employed as a lever) and that the rotatable journaling in their respective end holes is of such close tolerance that the combined effect of these two qualities of the model is such that any different directions of force applied to any two different rod ends would force the steel straps to yield into circular arc__then it will be clear that the three journaled end rods permit the three corner angles of the triangle to change to satisfy the resulting force or motion differential.

1103.02 If the rods in any one row in any one strap have their ends gathered toward one another, the strap will yield by curving its flat surfaces to the section of a cylinder whose axis is perpendicular to the plane of the rods. If all the rod ends of one strap are pulled together at one point (we refer to the one set of ends on either side of the strap), the strap, being equidistant along its center from that point, will form a segment of a circle, and each of the rods, being radii of that circle, will remain each perpendicular to the strap and all in a single plane perpendicular to the strap throughout the transformation.

1103.03 Now if all the ends of all the rods on one face side or the other of the triangle (since released to its original flat condition of first assembly), and if all of the three rows in the planes perpendicular to each of the three straps forming the triangle are gathered in a common point, then each of the three spring-steel-strap and rod sets will yield in separate arcs, and the three planes of rods perpendicular to them will each rotate around its chordal axis formed between the two outer rivet points of its arc, so that the sections of the planes on the outer side of the chords of the three arcs, forming what is now a constant-length, equiedged (but simultaneously changing from flat to arced equiedged), equiangled (but simultaneously altering corner-angled), spherical triangle, will move toward one another, and the sections of the planes on the inner side of the chords of the three arcs forming the constant, equiedged (but simultaneously changing flat-to-arc equiedged), and equiangled (but simultaneously altering corner-angled), spherical triangle will rotate away from one another. The point to which all rod ends are gathered will thus become the center of a sphere on the surface of which the three arcs occur, as arcs of great circles__for their planes pass through the center of the same sphere. The sums of the corner angles of the spherical triangles add to more than the 180 degrees of the flat triangle, as do all spherical triangles with the number of degrees and fractions thereof that the spherical triangle is greater than its chorded plane triangle being called the spherical excess, the provision of which excess is shared proportionately in each corner of the spherical triangle; the excess in each comer is provided in our model by the scissorslike angular increase permitted by the pivotal journals at each of the three corners of the steel- strap-edged triangle. (See Illus. 1101.02H.)

1103.04 The three arcs, therefore, constitute the edges of a spherical equilateral triangle, whose fixed-length steel boundaries are subdivided by the same uniform perimeter scale units of length as when the boundary lines were the "straight'' edge components of the flat triangle. Thus we are assured by our model that the original triangle's edge lengths and their submodular divisions have not been altered and that the finite closure of the triangle has not been violated despite its transformation from planar to spherical triangles.

1104.00 Constant Zenith of Flat and Spherical Triangles

1104.01 The radii of the sphere also extend outwardly above the surface arcs in equidistance, being perpendicular thereto, and always terminate in zenith points in respect to their respective points of unique penetration through the surface of the sphere.

1104.02 If we now release the rods from their common focus at the center of the sphere and the spring-steel straps return to their normal flatness, all the rods continue in the same perpendicularity to the steel bands throughout the transformation and again become parallel to one another and are grouped in three separate and axially parallel planes. What had been the external spherical zenith points remain in zenith in respect to each rod's point of penetration through the now flat triangle's surface edge. This is an important cartographic property2 of the transformational projection, which will become of increasing importance to the future high-speed, world-surface-unified triangulation through aerial and electromagnetic signal mapping, as well as to the spherical world- around data coordination now being harvested through the coordinately ``positioned" communications satellites "flying" in fixed formation with Earth. They and Moon together with Earth co-orbit Sun at 60,000 mph. (Footnote 2: In first contemplating the application of transformational projection for an Earth globe, I realized that the Basic Triangle __120 of which are the lowest common denominator of a sphere__would make a beautiful map. The reason I did not use it was because its sinuses intruded into the continents and there was no possible arrangement to have all the triangles' vertexes occur only in the ocean areas as in the vector equilibrium and icosahedral projection. The Basic LCD Icosahedral Triangle also has a spherical excess of only two degrees per corner, and there would have been no trouble at all to subdivide until the spherical excess for any triangle tile grid was approximately zero. Thus it could have been a 120-Basic-Triangle-grid, at a much higher frequency, but the big detriment was that the spherical trigonometry involved, at that time long before the development of a computer, was so formidable. So the icosahedron was adapted.)

1105.00 Minima Transformation

Fig. 1105.01

1105.01 If the rods are pushed uniformly through the spring-steel straps so that increasing or decreasing common lengths of rod extend on the side of the triangle where the rods are gathered at a common point, then, as a result, varying ratios of radii length in respect to the fixed steel-strap arc length will occur. The longer the rods, the larger will be the sphere of which they describe a central tetrahedral segment, and the smaller the relative proportional size of the spherical surface triangle bounded by the steel springs__as compared to the whole implicit spherical surface. Because the spherical triangle edge length is not variable, being inherent in the original length of the three identical steel springs, the same overall length can accommodate only an ever smaller spherical surface arc (central-angle subtension) whenever the radii are lengthened to produce a greater sphere.

1105.02 If the ends of the rods gathered together are sufficiently shortened, they will finally attain a minimum length adequate to reach the common point. This minimum is attained when each is the length of the radius of a sphere relative to which the steel spring's length coincides with the length of an arc of 120 degrees. This condition occurs uniquely in a spherical triangle where each of the three vertexes equals 180 degrees and each of the arcs equals 120 degrees, which is of course the description of a single great circle such as the equator.

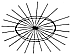Fig. 1105.03

1105.03 Constituting the minima transformation obtainable by this process of gathering of rod ends, it will be seen that the minima is a flat circle with the rods as spokes of its wheel. Obviously, if the spokes are further shortened, they will not reach the hub. Therefore, the minima is not 0__or no sphere at all__but simply the smallest sphere inherent in the original length of the steel springs. At the minima of transformation, the sphere is at its least radius, i.e., smallest volume.

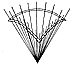Fig. 1105.04

1105.04 As the rods are lengthened again, the implied sphere's radius__ergo, its volume__grows, and, because of the nonyielding length of the outer steel springs, the central angles of the arc decrease, as does also the relative size of the equilateral, equiangular spherical triangle as, with contraction, it approaches one of the poles of the sphere of transformation. The axis running between the two poles of most extreme transformation of the spherical triangle we are considering runs through all of its transforming triangular centers between its__never attained__minimum-spherical-excess, smallest-conceivable, local, polar triangle on the ever-enlarging sphere, then reversing toward its largest equatorial, three- 180-degree-corners, hemisphere__area phase on its smallest sphere, with our triangle thereafter decreasing in relative spherical surface area as the__never attained__smallest triangle and the sphere itself enlarge toward the__also never attained__cosmically largest sphere. It must be remembered that the triangle gets smaller as it approaches one pole, the complementary triangle around the other pole gets correspondingly larger. It must also be recalled that the surface areas of both the positive and negative complementary spherical triangles together always comprise the whole surface of the sphere on which they co-occur. Both the positive and negative polar- centered triangles are themselves the outer surface triangles of the two complementary tetrahedra whose commonly congruent internal axis is at the center of the same sphere whose total volume is proportionately subdivided between the two tetrahedra.