1110.00 Zenith Constancy of Radial Coordination

1110.01 The zenith constancy of the transformational projection's topological trigonometry discretely locates the common zenith points of any commonly centered, concentric-surfaced systems.

1110.02 If camera-equipped telescopes were mounted aboard Earth-dispatched and - controlled satellites that were ``locked'' in fixed-formation flight positions around Earth, with one such fixed satellite hovering steadily over each vertex of a one-mile-edged world- triangulation grid, and if each telescope was trained so that the eyepiece of its eyepiece-to- optics' axis would be pointed exactly toward the center of Earth and its outer optics' end pointed exactly toward whatever star, if any, may be in exact zenith over the point on the surface of Earth above which the satellite was vertically positioned, a human on Earth at any of those points looking vertically outward into the heavens with a radarscope would discover that satellite as a blip in the middle of his scope-viewing tube's grid.

1110.03 Now let us have an around-the-world simultaneous clicking of the shutters of the cameras attached to each of the telescopes of each of those around-Earth, fixedly hovering photo-satellites with their telescopes pointed to whatever stars may be vertically outward from Earth at their respective omni-Earth-triangulated, one-mile-apart, grid vertexes. Let us assume the photographing telescopes to be very long-barreled to shield those not pointing at Sun from its intense luminosity. A composite mosaic of all those pictures could now be print-mounted spherically on the inside of a translucent 200-foot globe of Earth's conventional geographic data of continents, islands, etc., together with the conventional latitude-longitude grid. Because they were photographed outside Earth's cloud cover, they would present a composite and accurate spherical picture of what the navigators and astronauts call the celestial sphere, with the relative brilliance of the stars in evidence with astronomically calculatable corrections being made in the printing for the Sun's luminosity effects.

1110.04 While this picture was orientationally unique to its one moment in eternity in respect to the Earth-to-celestial-sphere orientation, Earth data per se and the celestial sphere data per se remain constant at their magnitude of scrutability within the lifespan of any human.

1110.05 Because of the accuracy with which this spherical picture was made, it would also be possible to take a transparent-plastic, 20-foot globe of Earth, with the latitude-longitude grid and the continents and islands outlined, together with the marker points identifying the respective positions of the satellite-mounted telescope cameras at the time of the photographing, and to position the 20-foot Earth globe within the 200-foot celestial sphere globe with the miniature Earth's spherical center congruent with the spherical center of the 200-foot celestial sphere.

1110.06 It is then possible to orient the miniature 20-foot-diameter Earth globe so that its polar axis is pointed toward the North Star, making a small correction to correspond with the astronomical correction for the small aberration well known to exist in this respect, which is negligible in this description of the properties of our triangular geodesics transformational projection. We may then rotate the miniature Earth 20-foot globe around its axis until a sighting from its exact center will register each of the satellite camera positions with each of the stars of the 200-foot celestial sphere that the satellites photographed in exact verticality outward from Earth.

1110.07 Earth's highest mountaintop is five miles above sea level, and the ocean's deepest bottom is five miles below sea level. We could now modify the surface of our transparent-plastic, 20-foot model of Earth to show these aberrations, which indicate that some parts of Earth's surface have a differential radial distance from Earth's center; but it would be in evidence that the stars would be in zenith over the same latitude-longitude grid points as would all of the satellite photographic stations.

1110.08 Finding that surface aberrations include only radial-distance variations and changes in the spherical-surface line-of-sight projections from the center, we will now introduce a clear-plastic shell model of a whale and of a crocodile, of such sizes that the crocodile is large enough to omnisurround or swallow the 20-foot miniature Earth globe, and that the whale is large enough to swallow the crocodile yet small enough to be inside the 200-foot-diameter, clear-plastic celestial sphere. With omnidirectional spoke-wires, we will now tensionally position the whale within the 200-foot celestial sphere, and we will tensionally wire-position the crocodile within the whale, and the 20-foot miniature Earth within the crocodile. The miniature Earth is oriented as before, its volumetric center exactly in congruence with the center of volume of the celestial sphere, with all of the stars at the time of the photographing in register with the same satellites that photographed them.

1110.09 Now the whale's and the crocodile's surfaces will be at a great variety of different radii distances from the concentric volumetric centers of the 200-foot and 20- foot spheres. We are going now to coat the surfaces of the transparent whale and transparent crocodile with a photosensitive emulsion. Then we have a high-intensity light source flash at the common volumetric centers of the 20-foot and 200-foot spheres. This process will reproduce on the plastic skin of both the whale and the crocodile__as well as on the celestial 200-foot sphere__the triangular satellite-positioning grid together with the latitude-longitude grid and all Earth's continental and insular outlines. Then, traveling with a pencil-beam strobic light on the outside of the 200-foot celestial sphere, we will point vertically inward against each of the stars, thus projecting their positions radially, i.e., vertically, inwardly to register on the skins of both the whale and the crocodile and on the 20-foot Earth globe. Now, with the human eye at the common concentric centers of volume of the 20-foot and 200-foot spheres, as well as both the whale and the crocodile, we may sight outwardly__which is inherently radially__in all directions, and observe that all the grids and all the geographical and celestial star data appear as one grid, being in exact radial register. We have all the same grids and data on all four of the concentric surfaces: 200-foot celestial sphere, whale, crocodile, and 20-foot Earth globe. That registering of all data is obviously independent of radial distance from the common center; ergo, the only variable in the system is the radius to any given point within the concentric systems.

1110.10 As we have demonstrated with geodesic domes and spheres, what is meant by compound curvature is "omni-intertriangulated structuring (i.e., balanced connectors) of concave-convex surface points." Given a unit radius sphere and the known central angle between any two radii of known length, then the length of the chord running between their outer ends may be calculated trigonometrically by running a line from the sphere center perpendicular to the mid-chord and solving for the right triangle thus formed, whose halved-chord outer edge is the side opposite its central angle, which is half the central angle originally given, and we know that the sine of an angle is the side opposite. When radius is assumed to be one, then the well-known sine of one-half the original angle given is the length of that half chord. With the chord length calculatable for a given central angle, it is easy to calculate the length of any line running between the outer end of one of the radii to a position on the other radius at a known distance outward from the spherical center. With this knowledge we can design struts, of suitable structural material__say, aluminum tubes__and we may triangularly interconnect all the vertex points of the triangular grid of the 200-foot sphere. Then we can triangularly interstrut all the grid points on the inside of the whale; then we can-interstrut all the grid vertexes of the crocodile; and finally we can intertriangularly strut the 20-foot Earth globe.

1110.11 Now again, viewing outwardly in all directions from the common volumetric centers of those concentric forms, we will see nothing changed because all the struts will be in register with all the lines of the four separate grids. If we now dissolve the plastic skins from all four shells__the 200-foot celestial sphere, the whale, the crocodile, and the 20-foot globe__we find that all four hold their shapes exactly as before and, being intertrussed (intertrussed and intertriangulated are the same words: truss: trace: and triangle) between vertexes of the grid, and the grid now being omnitriangularly interstructured, we may again sight outwardly from the volumetric center. A photograph of what we see will reveal only the same lines in exact register that we saw at the time of the original first spherical printing.

1110.12 Since the speed of light permitted astronauts to understand and adopt the light-year in their observational data, we have learned of the great variation of radial distances outwardly to the different stars. In the Big Dipper, one star is 200 light-years farther from Earth than the next one on the handle, which is a distance of 200 quadrillion miles farther away from you and me than is the other. If we ran rods radially from the volumetric center of our model outward perpendicularly through each of the stars shown on the 200-foot celestial sphere to a distance perpendicular outwardly from the 200-footer equal to their distance away in light-years from Earth, with the 200-foot sphere's 100-foot radius equaling that of the nearest star other than Sun, and assume that the camera had photographed only those stars visible to the naked eye, then a few of the rods would reach outwardly ten miles, but most of them would be much nearer in, with one of the Big Dipper's one mile out and another a half-mile out. It would make a vastly varied porcupine if we intertriangularly interconnected the outer terminals of the lines of interconnection, which would as yet be in exact register with the original grid as seen from system center.

1110.13 Now let us separate the four structures by opening up an approximate equator in the outer ones and rejoining the equatorial points. With this celestial porcupine rolled into our deepest ocean and then resting on the bottom, its top would reach outwardly above the ocean surface to the height of Mt. Everest; its densest, most high- frequency-trussed spherical core would be only 200 feet in diameter and would occur at ocean surface. The triangularly trussed 175-foot whale would hold its shape and size, as would the 60-foot crocodile and the little 20-foot miniature Earth. Obviously, they could not appear more differently.

1110.14 Our triangular geodesics transformation projection would show all four of these dissimilar systems in the flat plane in exactly the same manner and in exact register with that of Earth alone as shown later in the icosahedral flat-out of the world map, but with a number (or numbers of different styles) shown at each grid vertex, which number indicates the radius distance of that vertex outwardly from the center point of the system "Earth." Four different colors__blue for the celestial, black for the whale, green for the crocodile, and brown for the 20-foot Earth globe__would identify the relative radius distances outward from the congruent systems' center, which occurs at each vertex of these four utterly different-shaped and -sized systems__all on the same map. This would provide all of the data necessary to reconstruct each of the four systems in exactly the same relative sizes. Every point in the four systems remains in exact perpendicular (zenith), whether in the spherical or planar flat-out phase or any interim transitional phase. This makes possible the design of an airplane or an ocean liner all on one synergetic- geodesic map. And the flat-out map may have its triangular mosaic pieces rearranged in many ways__for instance, to center the oceans or to center the lands. And the building of that airplane or ocean liner, as with the geodesic dome, will generate compound curvature, omnifinite, tensegrity trussing far stronger and lighter than the presently designed and built XYZ-parallel coordinate grids and their parallel-plane sectional designing.

1110.15 With omnidirectional, complex, computerized, world-satellite sensing, comprehensive-resources inventorying and interrouting, the triangular geodesics transformational projection can alone bring visual comprehending and schematic-network elucidation.

1110.16 Just as triangular geodesics transformational projection can alone reduce the astronomical to the cosmic middle ground of eye-comprehensible coordination with the mind explorations and formulations in metaphysics in general and mathematics in particular, especially in relation to computer programming, so too may the triangular geodesics transformational projection enlarge the complex invisible microcosmic patterns to eye and sense comprehensibility.

1120.00 Wrapability

1120.01 One roll of paper being unrolled from any one fixed axis wraps up all the faces of a tetrahedron. Two rolls of paper being unrolled from two axes perpendicular to one another wrap up all the faces of the octahedron. Three rolls of paper being unrolled from three axes3* wrap up all the faces of the icosahedron. (Footnote 3: The six axes of the icosahedron are using the 12 vertexes coming together at 63° 26' to each other.)

1120.02 If the paper were transparent and there were ruled lines on the transparent paper at uniform single intervals, the single lines of the transparent paper wrapping up the tetrahedron will enclose the tetrahedron without any of the lines crossing one another. In wrapping up the octahedron with two rolls of such transparent paper, the lines cross__ making a grid of diamonds. Wrapping the icosahedron with the three rolls of transparent, parallel-ruled paper, a three-way grid of omnitriangulation appears.

1120.03 The wrapping of the six-edged tetrahedron with the single roll of paper leaves two opposite edges open, i.e., uncovered by the wrapping-paper roll. The other four opposite edges are closed, i.e., covered by the wrapping-paper roll.

1120.04 The wrapping of the 12-edged octahedron with two rolls of paper leaves two sets of opposite edges open. The other eight opposite edges are closed.

1120.05 The wrapping of the 30-edged icosahedron with three rolls of paper leaves three pairs of opposite edges open or uncovered. To cover those open edges, we need two more rolls. With five wrappings, all 30 edges become enclosed: with five wrappings, 10 faces are double-covered and 10 faces are triple-covered. Only the triple-covered have omnitriangular gridding by the parallel ruled lines. Thus we see that we need a sixth wrapping to make the omnitriangulated three-way grid. At the fifth wrapping, the three- way grid appears about the north and south poles with only a two-way grid on the equatorial triangles. The whole three-way grid six-times rewrapping in omnitriangular gridding at any desired frequency of subdivisioning can thus be accomplished with only one type of continuing, parallel-ruled strip.

1120.06 Wrapping relates to the mid-edges of prime structural systems.

1120.07 It takes three wrappings on three axes to produce the three-way grid on every face of a tetrahedron.

1120.08 Wrapping of the octahedron with two rolls of paper left two opposite edges open. Two strips covered all the faces. Three strips covered all the edges. But a fourth strip is needed to complete the omnitriangulation of each face of the octahedron. (Compare the four axes of the octahedron with the eight faces perpendicular to the center of volume of the octahedron. We are dealing with the axes of the mid-faces.) There are four unique ways to wrap an octahedron from a roll. The three-way grid for each face requires four-way wrappings.

1120.09 If we take a transparent sheet of paper whose width is the altitude of the equilateral triangles of the three universal prime structures, both of the edges can be stepped off with vectors of the same length. This produces a series of opposing, regular, uniform, equilateral triangles. The altitude of the equilateral triangle is the width of the transparent paper ruled with parallel lines parallel to the edges of the roll. Along the edge of one side of this roll, we step off increments the same length as the basic vectors of the triangles. We take the midpoint of the first triangle and drop a perpendicular across to the opposite edge of the roll. We step off increments of the same basic vector length. But the step-offs are staggered with the vertex of one triangle opposite the mid-edge of the other.

1120.10 This is how the lines of the tetrahedron keep wrapping up like a spool. That is why in the tetrahedron the axes are all the mid-edges of the poles. One polar pair of opposite edges is left open because the system is polarized; therefore, you need the three wrappings__one to cover all the faces, the second to cover all the edges, and the third for omnitriangulation. Three axes = three-way grid = three vectors for every vertex.

1120.11 A single wrapping defines the octahedron even though two faces are left uncovered. It is polarized by the empty opposite triangles. One-half vector lacks rigidity. The interference of two planes is required for the spin. But we have to deal with open edges as well as with open faces. The figure will stand stably because six of the 12 edges are double-spin, with two edges coming together in dihedral angles.

1120.12 Because one preomnitriangulated strip whose width exactly equals the altitude of the tetrahedron can completely spool-wrap all four faces of the tetrahedron, and because a tetrahedron so wrapped has an axis running perpendicular to__and outward through__the two mid-unwrapped-edges of the tetrahedron spool, such a spool may be endlessly wrapped, being a tetrahedron and an omnidirectionally closed system; ergo all the data of evoluting inwardly and outwardly in observable Universe and its scenario of intertransformings could be continuously rephotographed with each cycle and could thus be fed linearly into__and stored in__a computer in the most economical manner to be recalled and rerun, thus coping with all manner of superimpositions and inclusions at recorded dial distances inward and outward as a minimal-simplicity device.

1130.00 Omnidirectional Typewriter

[1130.00-1133.04 Typewriter Scenario]

1130.10 Model Studies

1130.11 Hypothetical model studies are schematic probability studies . Some are planar area models, but many deal exclusively with linear probability. Comprehensive reality problems are not linear; they are omnidirectional. They deal with total system and total Universe. That is what world society is not attending to realistically and that's why we are in trouble: Synergy shows that you cannot solve comprehensive problems with exclusively local planar or local linear models.

1130.20 Orbital Feedback Circuitry vs Critical Path

1130.21 Conventional critical-path conceptioning is linear and self-under-informative. Only orbital system feedbacks are both comprehensively and incisively informative. Orbital critical feedback circuits are pulsative, tidal, importing and exporting. Critical-path elements are not overlapping linear modules in a plane: they are interspiralling complexes of regenerative feedbacks or circuits.

1130.22 When we go out to the Earth-orbiting Moon and plan to get back into the biospheric-enshrouded Earth again, we are dealing in 60,00-miles-per-hour solar system spiraling as the solar system while part of our galaxy rotates around the galaxy center at 700,000 miles per hour. This, altogether with the intergalactic motion, means we can never come back to where we were even though we safely reach Earth.

1130.23 People may think they are being realistically linear, but they are actually just increasing the radius of larger and larger spiral orbits. Each year is a Sun-spiraling circuit. Years are not linear. As humans complete their daily local circuits, the Earth spins about its axis and orbits the Sun; wherefore the critical path of progressive accomplishment that led to humans reaching the Moon and returning safely to Earth involves not a linear months-and-years progression but a complex of millions of spirals within spirals. With each year the multimillion-stranded rope of omniinterrelated local circuitry feedback closures integrates synergetically to produce a spirally orbiting, complex, system-defining set of Sun-Earth-Moon orbiting events, and this system finally reaches out to embrace the Moon as well as the Earth, all of which ever expands humanity's local Universe involvement. (See Sec. 535.20.)

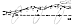Fig. 1130.24

1130.24 A structural system (even such a structural system as a building) can be thought of as a multi-great-circle-faced clock, a complex of feedback circuitry where the sum-total of interferences of the pushes and pulls are everywhere synergetically and locally regenerative. As the humans complete their daily local circuits, the Earth spins about its axis and concurrently orbits the Sun; wherefore the critical spiral path of progressive accomplishment that led to humans reaching the Moon and returning safely to Earth involves not a linear months-and-years progression but a complex of millions of spirals within spirals of an around-the-Sun-by-Earth orbiting and an around-the-Earth-by-Moon orbiting progression, wherein we progressively establish one feedback circuitry system overlapping another, and another, and so on as the year goes around.

1130.25 The reality is always systematically spiro-orbital. Orbit = circuit. For instance, all terrestrial critical-path developments inherently orbit the Sun. No path can develop as curvature-free linearity. All paths are precessionally modulated by remotely operative forces that produce curvi-wavi-spiralinear paths. Increasingly complex curvi- wavi-spiralinear, system-embracing circuits are diffusive__ergo, spinoff prone; ergo, system-mass reducing; ergo, ultimately bit-by-bit self-annihilative. Spun-off simplexes may come into critical interattractiveness with other diffusely detached simplexes to form other young complex systems, to syntropically initiate new, mass-increasing, cosmically-local- traveler, complex system-defining, new intercelestial orbiting circuits.