535.00 Halo Concept

535.01 The phenomenon "infinity" of the calculus is inherently finite (see Sec. 224.11). Universe is nonsimultaneous but finite, because all experiences begin and end, and being terminal, are finite; ergo, Universe as the sum of finites is finite.

535.02 Nonsimultaneous Universe is finite but conceptually undefinable; local systems are definable. We discover that Universe is finite and a local system is definite; every definite local system has inherent, always and only co-occurring twoness of polar axis spinnability and twoness of concave-convex complementary disparity of energy interaction behavior,4 plus two invisible tetrahedra (or two unities), altogether adding together as equal finitely fourfold symmetry Universe. The difference between Universe and any local system is always two invisible tetrahedra. Every local system may be subdivided into whole tetrahedra.

(Footnote 4: Concave concentrates radiation; convex diffuses radiation.)

535.03 Finite minus de-finite means four tetrahedra minus two tetrahedra. Finite Universe equals eight cyclic unities. Every tetrahedron equals two, having inside- outingness oscillatory transformability unavailable to any structural system other than the tetrahedron.

535.04 Halo conceptioning discloses the minute yet finitely discrete inaccuracy of the fundamental assumption upon which calculus was built; to wit, that for an infinitesimal moment a line is congruent with the circle to which it is tangent and that a plane is congruent with the sphere to which it is tangent. Calculus had assumed 360 degrees around every point on a sphere. The sum of a sphere's angles was said to be infinite. The halo concept and its angularly generated topology proves that there are always 720 degrees, or two times unity of 360 degrees, less than the calculus' assumption of 360 degrees times every point in every "spherical" system. This 720 degrees equals the sum of the angles of a tetrahedron. We can state that the number of vertexes of any system (including a "sphere," which must, geodesically, in universal-energy conservation, be a polyhedron of n vertexes) minus two times 360 degrees equals the sum of the angles around all the vertexes of the system. Two times 360 degrees, which was the amount subtracted, equals 720 degrees, which is the angular description of the tetrahedron. We have to take angular "tucks" in the nonconceptual finity (the calculus infinity). The "tucks" add up to 720 degrees, i.e., one tetrahedron. The difference between conceptual de-finity and nonconceptual finity is one nonconceptual, finite tetrahedron.

535.05 In the general theory of variables, it has been recognized that the set of all the variables may be divided into two classes: (1) the class of all the inclusive variables within a given system, the interior relevants, and (2) the class of all those operative exclusive of the system, the exterior relevants. It has been further recognized that the variables outside the system may affect the system from outside. In varying degrees, specific levels of subclasses of these "background" or outside variables are identified as parameters. But the "background" concept is fallaciously inadequate; dealing with insideness and outsideness for "background" is limited to the two-dimensional or flat- projection concept, which inherently lacks insideness__ergo, cannot also have outsideness, which always and only coexists with insideness. Ergo, all two-dimensional copings with systems are inherently inadequate and prophetically vitiated.

535.06 Our omnioriented halo concept converts the parameter consideration to symmetrically conceptual four-dimensionality and discloses a set of parameters inside as well as outside the zone of lucidly considered system stars. And the parameters are, at minimum, fourfold: the concave twilight zone of inward relevancy; the convex twilight zone of outward relevancy; the stark, nonconceptual irrelevancy inward; and the stark, nonconceptual irrelevancy outward. Parameter 1 is a visible tetrahedron. Parameter 2 is a visible tetrahedron. Parameter 3 is an invisible tetrahedron. Parameter 4 is an invisible tetrahedron.

535.07 The considered relevancy within the zone of lucidity consists of one tetrahedron or more. For each "considered tetrahedron," there are three complementary always and only co-occurring parametric tetrahedra. We discover that our omnihalo epistemological accounting consists entirely of rational tetrahedral quantation.

535.08 By the omnidirection, star-studded halo reasoning, the development of a conceptual tetrahedron automatically changes a negative yet invisible tetrahedron into the nonsimultaneous, nonconceptual, finite Universe, comprehensive to the local de-finite conceptual system.

535.09 The halo concept is that of an omnidirectional, complex, highfrequency, Doppler-effected, hypothetical zone experience in an omnidirectional, universal maelstrom of nonsimultaneous near and far explosions and their interaccelerating and refractive wave-frequency patternings and complex, precessionally-induced, local orbitings. The omni-interactions impinge on your nervous system in all manner of frequencies, some so "high" as to appear as "solid" things, some so slow as seeming to be "absolute voids."

535.10 Spherical Structures

535.11 Because spherical sensations are produced by polyhedral arrays of interferences identified as points approximately equidistant from a point at the approximate center, and because the mass-attractive or -repulsive relationships of all points with all others are most economically shown by chords and not arcs, the spherical array of points is all interconnected triangularly by the family of generalized principles being operative as Universe, which produces very-high-frequency, omnitriangulated geodesic structures, which are an aggregate of chords triangularly interconnecting all the nearestly-surrounding points whose vertexly-converging angles always add up to less than 360°.

535.20 Building

535.21 A building can be thought of as a clock, i.e., as a feedback circuitry wherein local pushings and pullings are structurally regenerative and ever-self-restabilizing. The spirally overlapping critical path of progressive accomplishments that led to humans reaching the Moon and returning safely to Earth involved not a linear months-and-years progression but an around-the-Sun-by-Earth orbiting and an around-the-Earth-by-Moon orbiting progression of accomplished events wherein humans progressively established one feedback circuitry system overlapping another, and another, more than a million times, as the year of Earth-Moon orbiting of 365 axially-rotated-in-orbit days drew to orbital close at a galactic merry-go-round repositioning in the cosmic theater that finds the planet Earth and its 92-million-miles-away Sun six billion miles away from where their Earth-Sun year began. And all of these celestially complex "goings-on" had to be competently comprehended and attended in order for humans to ferry both outward and returning between the complexedly moving Earth and the ever-more-complexedly orbiting, spinning, and galaxying Sun-Earth-Moon team.

535.22 Thus with each year the spiraled critical-path "rope" of omniinterrelated, locally overlapping, circuitry-feedback closures integrated synergetically to produce the finally realized Earth-Moon inter-round-tripping of humans as the whole show co-orbited the Sun. The entire complex operation resulted in an ever-expanding spontaneous involvement of Earthians in an ever-increasing range of local Universe affairs. (See Sec. 1130.20.)

536.00 Interference Domains of Structural Systems

536.01 As distinct from other mathematics, synergetics provides domains of interferences and domains of crossings. In the isotropic vector matrix, the domains of vertexes are spheres, and the domains of spheres are rhombic dodecahedra. These are all the symmetries around points. Where every vertex is the domain of a sphere we have closest-rhombic-dodecahedral-packing.

536.02 The coordinate system employed by nature uses 60 degrees instead of 90 degrees, and no lines go through points. There are 60-degree convergences even though the lines do not go through a point. The lines get into critical proximities, then twist-pass one another and there are domains of the convergences.

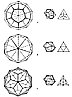Fig. 536.03

536.03 In a polyhedral system, critical-proximity-interference domains are defined by interconnecting the adjacent centers of area of all the separate superficial faces, i.e., "external areas" or "openings," surrounding the vertex, or "crossing." The surface domain of a surface vertex is a complex of its surrounding triangles: a hexagon, pentagon, or other triangulated polygon. (See Sec. 1006.20.)

536.10 Domains of Volumes

536.11 There are domains of the tetrahedron interfaced (triple-bonded) with domains of the octahedron. The domains of both are rationally subdivided into either A or B Modules. There is the center of volume (or gravity) of the tetrahedron and the center of volume (or gravity) of the octahedron, and the volumetric relationship around those centers of gravity is subdivisible rationally by A and B Quanta Modules5 in neat integer whole numbers. I can then speak of these domains quantitatively without consideration of now obsolete (superficial) face surfaces, i.e., polyhedra. Even though the cork is not in the bottle, I can speak quantitatively about the contents of the bottle. This is because it is a domain even though the edge-surrounded opening is uncorked. So we have no trouble topologically considering tensegrity mensuration. It is all open work, but its topological domains are clearly defined in terms of the centers of the systems involved having unique, centrally angled insideness and surface-angle-defined outsideness.

(Footnote 5: See Sec. 920.)

536.20 Domain of an Area

536.21 Areas do not have omnidirectional domains. The domain of an area is the area itself: it is the superficial one that man has looked at all these centuries. The domain of a face is a triangle in the simplest possible statement. Thus the domain of each face of the icosahedron is the triangular face itself.

536.30 Domain of a Line

536.31 The domains of the vector edges are defined by interconnecting the two centers of area of the two surface areas divided by the line with the ends of the line. The edge dominates an area on either side of it up to the centers of area of the areas it divides. Therefore, they become diamonds, or, omnidirectionally, octahedra. The domains of lines are two tetrahedra, not one octahedron.

536.32 The domains of lines must be two triple-bonded (face-bonded) tetrahedra or one octahedron. There could be two tetrahedra base-to-base, but they would no longer be omnisymmetrical. You can get two large spheres like Earth and Moon tangent to one another and they would seem superficially to yield to their mass attractiveness dimpling inward of themselves locally to have two cones base to base. But since spheres are really geodesics, and the simplest sphere is a tetrahedron, we would have two triangles base to base__ergo, two tetrahedra face-bonded and defined by their respective central angles around their two gravity centers.

536.33 The domain of each edge of the icosahedron is a diamond formed by connecting the vertexes of two adjacent icosahedron-face triangles with their centers of area.

536.40 Domain of a Point

536.41 Looking at a vector equilibrium as unity, it is all the domain of a point with a volume of 480.

536.42 The domains of points as vertexes of systems are tetrahedra, octahedra, or triangulated cubes. Or they could be the A and B Modules formed around the respective polyhedra.

536.43 The most complete description of the domain of a point is not a vector equilibrium but a rhombic dodecahedron, because it would have to be allspace filling and because it has the most omnidirectional symmetry. The nearest thing you could get to a sphere in relation to a point, and which would fill all space, is the rhombic dodecahedron.

536.44 A bubble is only a spherical bubble by itself. The minute you get two bubbles together, they develop a plane between them.

536.50 Domains of Actions

536.51 There are critical proximities tensionally and critical proximities compressionally__that is, there are attractive fields and repelling fields, as we learn from gravity and electromagnetics. There are domains or fields of actions. In gases under pressure, the individual molecules have unique atomic component behaviors that, when compressed, do not allow enough room for the accelerated speeds of their behavior; the crowded and accelerating force impinges upon the containing membrane to stretch that membrane into maximum volume commensurate with the restraints of its patterned dimensions.