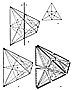
Fig. 987.230 		987.230 Symmetries #1 & 3; Cleavages #1 & 2
987.231 Of the seven equatorial symmetries first employed in the progression of self- fractionations or cleavages, we use the tetrahedron's six mid-edge poles to serve as the three axes of spinnability. These three great-circle spinnings delineate the succession of cleavages of the 12 edges of the tetra-contained octahedron whose six vertexes are congruent with the regular tetrahedron's six midedge polar spin points. The octahedron resulting from the first cleavage has 12 edges; they produce the additional external surface lines necessary to describe the two-frequency, non-time-size subdividing of the primitive one-frequency tetrahedron. (See Sec. 526.23, which describes how four happenings' loci are required to produce and confirm a system discovery.)
987.232 The midpoints of the 12 edges of the octahedron formed by the first cleavage provide the 12 poles for the further great-circle spinning and Cleavage #2 of both the tetra and its contained octa by the six great circles of Symmetry #3. Cleavage #2 also locates the center-of-volume nucleus of the tetra and separates out the center-of-volume- surrounding 24 A Quanta Modules of the tetra and the 48 B Quanta Modules of the two- frequency, tetra-contained octa. (See Sec. 942 for orientations of the A and B Quanta Modules.)

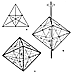Fig. 987.240 		987.240 Symmetry #3 and Cleavage #3

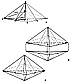Fig. 987.241 		987.241 Symmetry #3 and Cleavage #3 mutually employ the six-polar-paired, 12 midedge points of the tetra-contained octa to produce the six sets of great-circle spinnabilities that in turn combine to define the two (one positive, one negative) tetrahedra that are intersymmetrically arrayed with the common-nuclear-vertexed location of their eight equi-interdistanced, outwardly and symmetrically interarrayed vertexes of the "cube"__the otherwise nonexistent, symmetric, square-windowed hexahedron whose overall most economical intervertexial relationship lines are by themselves unstructurally (nontriangularly) stabilized. The positive and negative tetrahedra are internally trussed to form a stable eight-cornered structure superficially delineating a "cube" by the most economical and intersymmetrical interrelationships of the eight vertexes involved. (See Fig. 987.240.)

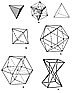Fig. 987.242 		987.242 In this positive-negative superficial cube of tetravolume-3 there is combined an eight-faceted, asymmetric hourglass polyhedron of tetravolume-l½, which occurs interiorly of the interacting tetrahedra's edge lines, and a complex asymmetric doughnut cored hexahedron of tetravolume 1½, which surrounds the interior tetra's edge lines but occurs entirely inside and completely fills the space between the superficially described "cube" defined by the most economical interconnecting of the eight vertexes and the interior 1½-tetravolume hourglass core. (See Fig. 987.242E987.242E.)
987.243 An illustration of Symmetry #3 appears at Fig. 455.11A.
987.250 Other Symmetries
987.251 An example of Symmetry #4 appears at Fig. 450.10. An example of Symmetry #5 appears at Fig. 458.12B. An example of Symmetry #6 appears at Fig. 458.12A. An example of Symmetry #7 appears at Fig. 455.20.
987.300 Interactions of Symmetries: Spheric Domains
987.310 Irrationality of Nucleated and Nonnucleated Systems
987.311 The six great circles of Symmetry #3 interact with the three great circles of Symmetry # 1 to produce the 48 similar-surface triangles ADH and AIH at Fig. 987.21ON. The 48 similar triangles (24 plus, 24 minus) are the surface-system set of the 48 similar asymmetric tetrahedra whose 48 central vertexes are congruent in the one__VE's__nuclear vertex's center of volume.

Fig. 987.312 		987.312 These 48 asymmetric tetrahedra combine themselves into 12 sets of four asymmetric tetra each. These 12 sets of four similar (two positive, two negative) asymmetric tetrahedra combine to define the 12 diamond facets of the rhombic dodecahedron of tetravolume-6. This rhombic dodecahedron's hierarchical significance is elsewhere identified as the allspace-filling domain of each closest-packed, unit-radius sphere in all isotropic, closest-packed, unit-radius sphere aggregates, as the rhombic dodecahedron's domain embraces both the unit-radius sphere and that sphere's rationally and exactly equal share of the intervening intersphere space.
987.313 The four great circles of Symmetry #2 produce a minimum nucleated system of 12 unit-radius spheres closest packed tangentially around each nuclear unit-radius sphere; they also produce a polyhedral system of six square windows and eight triangular windows; they also produce four hexagonal planes of symmetry that all pass through the same nuclear vertex sphere's exact center.
987.314 These four interhexagonalling planes may also be seen as the tetrahedron of zero-time-size-volume because all of the latter's equi-edge lengths, its face areas, and system volumes are concurrently at zero.
987.315 This four-great-circle interaction in turn defines the 24 equilengthed vectorial radii and 24 equi-lengthed vector chords of the VE. The 24 radii are grouped, by construction, in two congruent sets, thereby to appear as only 12 radii. Because the 24 radial vectors exactly equal energetically the circumferentially closed system of 24 vectorial chords, we give this system the name vector equilibrium. Its most unstable, only transitional, equilibrious state serves nature's cosmic, ceaseless, 100-percent-energy- efficient, self-regenerative integrity by providing the most expansive state of intertransformation accommodation of the original hierarchy of primitive, pre-time-size, "click-stop" rational states of energy-involvement accountabilities. Here we have in the VE the eight possible phases of the initial positive-negative tetrahedron occurring as an inter-double-bonded (edge-bonded), vertex-paired, self-inter-coupling nuclear system.
987.316 With the nucleated set of 12 equi-radius vertexial spheres all closest packed around one nuclear unit-radius sphere, we found we had eight tetrahedra and six Half- octahedra defined by this VE assembly, the total volume of which is 20. But all of the six Half-octahedra are completely unstable as the 12 spheres cornering their six square windows try to contract to produce six diamonds or 12 equiangular triangles to ensure their interpatterning stability. (See Fig. 987.240.)
987.317 If we eliminate the nuclear sphere, the mass interattraction of the 12 surrounding spheres immediately transforms their superficial interpatterning into 20 equiangular triangles, and this altogether produces the self-structuring pattern stability of the 12 symmetrically interarrayed, but non-spherically-nucleated icosahedron.
987.318 When this denucleation happens, the long diagonals of the six squares contract to unit-vector-radius length. The squares that were enclosed on all four sides by unit vectors were squares whose edges__being exactly unity__had a diagonal hypotenuse whose length was the second root of two__ergo, when VE is transformed to the icosahedron by the removal of the nuclear sphere, six of its sqrt(2)-lengthed, interattractive-relationship lines transform into a length of 1, while the other 24 lines of circumferential interattraction remain constant at unit-vector-radius length. The difference between the second root of two (which is 1.414214 - 1, i.e., the difference is 0.414214) occurs six times, which amounts to a total system contraction of 2.485284. This in turn means that the original
24 + 8.485284 = 32.485284
overall unit-vector-lengths of containing bonds of the VE are each reduced by a length of 2.485284 to an overall of exactly 30 unit-vector-radius lengths.
987.319 This 2.485284 a excess of gravitational tensional-embracement capability constitutes the excess of intertransformative stretchability between the VE's two alternatively unstable, omnisystem's stable states and its first two similarly stable, omnitriangulated states.
987.320 Because the increment of instability tolerance of most comprehensive intertransformative events of the primitive hierarchy is an irrational increment, the nucleus- void icosahedron as a structural system is inherently incommensurable with the nucleated VE and its family of interrational values of the octahedral, tetrahedral, and rhombic dodecahedral states.
987.321 The irrational differences existing between nucleated and nonnucleated systems are probably the difference between proton-nucleated and proton-neutron systems and nonnucleated-nonneutroned electron systems, both having identical numbers of external closest-packed spheres, but having also different overall, system-domain, volumetric, and system-population involvements.
987.322 There is another important systemic difference between VE's proton-neutron system and the nonnucleated icosahedron's electron system: the icosahedron is arrived at by removing the nucleus, wherefore its contraction will not permit the multilayering of spheres as is permitted in the multilayerability of the VE__ergo, it cannot have neutron populating as in the VE; ergo, it permits only single-layer, circumferential closest packings; ergo, it permits only single spherical orbiting domains of equal number to the outer layers of VE-nucleated, closest-packed systems; ergo, it permits only the behavioral patterns of the electrons.
987.323 When all the foregoing is comprehended, it is realized that the whole concept of multiplication of information by division also embraces the concept of removing or separating out the nucleus sphere (vertex) from the VE's structurally unstable state and, as the jitterbug model shows, arriving omnisymmetrically throughout the transition at the structural stability of the icosahedron. The icosahedron experimentally evidences its further self-fractionation by its three different polar great-circle hemispherical cleavages that consistently follow the process of progressive self-fractionations as spin- halved successively around respective #5, #6, and #7 axes of symmetry. These successive halvings develop various fractions corresponding in arithmetical differentiation degrees, as is shown in this exploratory accounting of the hierarchy of unit-vector delineating multiplication of information only by progressive subdividing of parts.
987.324 When the tetrahedron is unity of tetravolume-1 (see Table 223.64), then (in contradistinction to the vector-radiused VE of tetravolume-20)
__ the vector-diametered VE = + 2½ or = - 2½
__ a rational, relative primitive prime number S tetravolume is also only realizable with half of its behavioral potentials in the presently-tune-in-able macrocosm and the other half of its total 5 behavioral potential existent in the presently-tune-out-able microcosm; thus,
__ an overall +5 tetravolume potential -2½__ergo, +5 - 2½ = +2½
or
__ an overall -5 tetravolume potential +2½ __ergo, - 5+2½ = - 2½
987.325 The positive and negative tetrahedra, when composited as symmetrically concentric and structurally stable, have eight symmetrically interarranged vertexes defining the corners of what in the past has been mistakenly identified as a primitive polyhedron, popularly and academically called the "cube" or hexahedron. Cubes do not exist primitively because they are structurally unstable, having no triangularly-self-stabilizing system pattern. They occur frequently in nature's crystals but only as the superficial aspect of a conglomerate complex of omnitriangulated polyhedra.

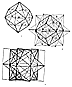Fig. 987.326 		987.326 This positive-negative tetrahedron complex defines a hexahedron of overall volume-3__1½ inside and 1½ outside its intertrussed system's inside-and-outside-vertex-defined domain.
__ The three-great-circle symmetrical cleavaging (#I) of the primitive tetrahedron produces the vector-edged octahedron of tetravolume-4.
__ The vector-radiused rhombic triacontahedron, with its .9994833324 unit-vector- radius perpendicular to its midface center produces a symmetrical polyhedron of tetravolume-5.
__ With its 12 diamond-face-centers occurring at unit-vector-radius, the rhombic dodecahedron has a tetravolume-6.
The rhombic dodecahedron exactly occupies the geometric domain of each unit-vector- radius sphere and that sphere's external share of the symmetrically identical spaces intervening between closest-packed unit-radius spheres of any and all aggregates of unit- radius, closest-interpacked spheres. In this closest-packed condition each sphere within the aggregate always has 12 spheres symmetrically closest packed tangentially around it. The midpoints of the 12 diamond faces of the rhombic dodecahedron's 12 faces are congruent with the points of tangency of the 12 surrounding spheres. All the foregoing explains why unit-radius rhombic dodecahedra fill allspace when joined together.
987.327 Repeating the foregoing more economically we may say that in this hierarchy of omnisymmetric primitive polyhedra ranging from I through 2, 2 , 3, 4, 5, and 6 tetravolumes, the rhombic dodecahedron's 12 diamond-face-midpoints occur at the points of intertangency of the 12 surrounding spheres. It is thus disclosed that the rhombic dodecahedron is not only the symmetric domain of both the sphere itself and the sphere's symmetric share of the space intervening between all closest-packed spheres and therefore also of the nuclear domains of all isotropic vector matrixes (Sec. 420), but the rhombic dodecahedron is also the maximum-limit-volumed primitive polyhedron of frequency-l.
Next Section: 987.400
Copyright © 1997 Estate of R. Buckminster Fuller