
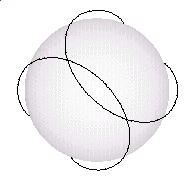
We show in the pattern on a torus movies that the pattern can pass through itself. This is also mentioned in the section showing the pattern "breathing".
The important point here is that when the pattern passes through itself, it changes its orientaion by 90 degrees. This is shown in the following two "snap shots" from the pattern breathing movies.

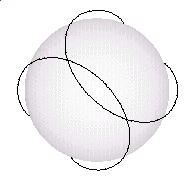
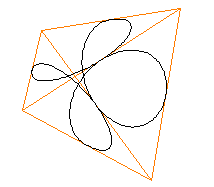
In the section on the construction of the pattern on a tetrahedron I showed that the pattern, when fully opened, fits exactly onto the 4 faces of a tetrahedron.
Now we will put two tetrahedron together with one tetrahedron rotated by 90 degrees.
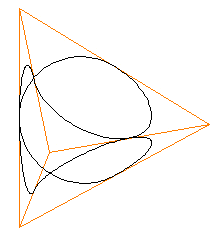
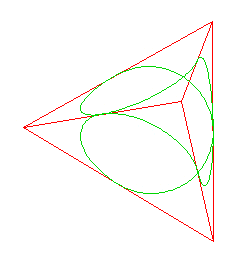
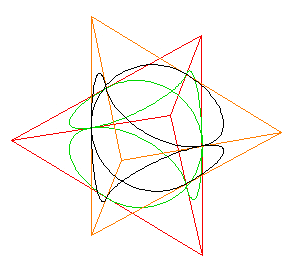
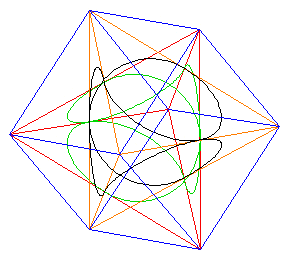
You can see that by its "breathing" motion (and limits), Lynnclaire's knot pattern,
One starts to wonder what dosen't this knot define!
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.