
We know that the symmetry axis of a Tetrahelix passing through a Tetrahedron's triangular face must pass through a triangle face coordinate (7, 3). (See this web page for details.)
We highlight the 3 (7,3) traingle face coordinates by drawing a red triangle.

We divide all 4 faces of the Tetrahedron into a 10-frequency grid and draw the (7,3) tirangles in red.

We next connect all the vertices of the red triangles to all other red triangle vertices.
Since we know that the Tetrahelix symmetry axis passes into a Tetrahedron and out of a Tetrahedron through only these (7,3) positions, some of these lines must be the symmetry axes for all possible Tetrahelix passing through this Tetrahedron.

We also know that this symmetry axis passes by the center of volume of the Tetrahedron at a distance of (sqrt(2)/10)EL. (See this web page for details.)
So we place a sphere with this radius value at the center of volume of the Tetrahedron.

The lines which pass the sphere at a tangent point on the sphere will be a symmetry axis for a Tetrahelix. These lines will be shown in green.



There are 12 green lines, so there are 12 Tetrahelix passing through a single Tetrahedron. Six of these will have a Clockwise screw sense and 6 will have a Counter Clockwise screw sense.
It would be very interesting to know what breaks the symmetry of screw sense. How is it that one green line gets assigned to a Clockwise screw sense Tetrahelix and another gets assigned to a Counter Clockwise? At this point, one line seems the same as any other line.
Note that the green lines come in crossing pairs. There are 6 intersetion points which define an Octahedron.
The angle of the interseting green lines gives the angle at which the Tetrahelix intersect ech other.

However, it should be noted that the symmetry axis of two Tetrahelix which share the same Tetrahedron do not have to intersect inside the shared Tetrahedron.
As the following figure shows, a Tetrahelix's symmetry axis will intersect 5 other Tetrahelix axis of symmetry and 2 of the intersection points are outside the Tetrahedron.
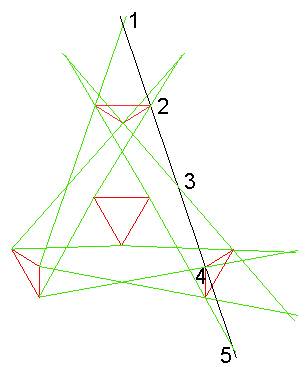
Intersection points 1 and 5 in the above figure are outside the Tetrahedron. Points 2 and 4 are on the face of the Tetrahedron and intersection point 3 is inside the Tetrahedron.
It has been suggested to me by Joe Matto that 2 Tetrahelix can "intersect" each other at 90 degrees. This is not possible if by "intersect" one means that the axis of symmetry of the Tetrahelix intersect at 90 degrees.
However, recall that the opposite edge of a Tetrahedron pass by each other at 90 degrees. That is, the two opposit edges share the same mid-edge point axis and one edge is rotated by 90 degrees about this shared axis with respect to the other edge.
In a similar way, the axis of symmetry of 2 Tetrahelix can pass by each other at 90 degrees. Note that the 2 Tetrahelix are also passing through the same Tetrahedron. So, one could say that the Tetrahelix are intersecting each other at 90 degrees.
Here is a figure showing the symmetry axis lines from another point of view showing that one passes under another and are rotated about a common axis by 90 degrees, just like the Tetrahedron case shown above.


Here is another perspective of this in which I draw in a Tetrhaheron (in black) and a mid-edge to mid-edge axis of the Tetrahedron (in blue).

More details and calculations are given on the next page.
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.