
 Closest Packing of Rods
Closest Packing of Rods

|
412.00  Closest Packing of Rods
Closest Packing of Rods
|
 Fig. 412.01 |
412.01
 Just as six balls may be closest packed around a nuclear
ball in a plane, six
rods or wires may be closest packed around a nuclear
rod or wire in a cluster. When the
seven wires are thus compacted in a parallel bunch,
they may be twisted to form a cable of
hexagonal cross section, with the nuclear wire surrounded
by the other six. The hexagonal
pattern of cross section persists as complete additional
layers are symmetrically added to
the cluster. These progressive symmetrical surroundments
constitute circumferentially
finite integrities in universal geometry.
Just as six balls may be closest packed around a nuclear
ball in a plane, six
rods or wires may be closest packed around a nuclear
rod or wire in a cluster. When the
seven wires are thus compacted in a parallel bunch,
they may be twisted to form a cable of
hexagonal cross section, with the nuclear wire surrounded
by the other six. The hexagonal
pattern of cross section persists as complete additional
layers are symmetrically added to
the cluster. These progressive symmetrical surroundments
constitute circumferentially
finite integrities in universal geometry.
|

|
412.02
 Surface Tension Capability: We know by conclusive
experiments and
measuring that the progressive subdivision of a given
metal fiber into a plurality of
approximately parallel fibers provides tensile behavior
capabilities of the smaller fibers at
increased magnitudes up to hundreds- and thousandsfold
that of the unit solid metal
section. This is because of the increased surface-to-mass
ratios and because all high tensile
capability is provided by the work hardening of the
surfaces. This is because the surface
atoms are pressed into closer proximity to one another
by the drawing tool through which
the rod and wire are processed.
Surface Tension Capability: We know by conclusive
experiments and
measuring that the progressive subdivision of a given
metal fiber into a plurality of
approximately parallel fibers provides tensile behavior
capabilities of the smaller fibers at
increased magnitudes up to hundreds- and thousandsfold
that of the unit solid metal
section. This is because of the increased surface-to-mass
ratios and because all high tensile
capability is provided by the work hardening of the
surfaces. This is because the surface
atoms are pressed into closer proximity to one another
by the drawing tool through which
the rod and wire are processed.
|

|
413.00
 Omnidirectional Closest Packing
Omnidirectional Closest Packing
|
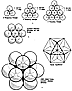 Fig. 413.01 |
413.01
 In omnidirectional closest packing of equiradius spheres
around a nuclear
sphere, 12 spheres will always symmetrically and intertangentially
surround one sphere
with each sphere tangent to its immediate neighbors.
We may then close-pack another
symmetrical layer of identical spheres surrounding the
original 13. The spheres of this
outer layer are also tangent to all of their immediate
neighbors. This second layer totals 42
spheres. If we apply a third layer of equiradius spheres,
we find that they, too, compact
symmetrically and tangentially. The number of spheres
in the third layer is 92.
In omnidirectional closest packing of equiradius spheres
around a nuclear
sphere, 12 spheres will always symmetrically and intertangentially
surround one sphere
with each sphere tangent to its immediate neighbors.
We may then close-pack another
symmetrical layer of identical spheres surrounding the
original 13. The spheres of this
outer layer are also tangent to all of their immediate
neighbors. This second layer totals 42
spheres. If we apply a third layer of equiradius spheres,
we find that they, too, compact
symmetrically and tangentially. The number of spheres
in the third layer is 92.
|

|
413.02
 Equiradius spheres closest packed around a nuclear
sphere do not form a
supersphere, as might be expected. They form a symmetrical
polyhedron of 14 faces: the
vector equilibrium.
Equiradius spheres closest packed around a nuclear
sphere do not form a
supersphere, as might be expected. They form a symmetrical
polyhedron of 14 faces: the
vector equilibrium.
|

|
413.03
 If we add on more layers of equiradius spheres to
the symmetrical
polyhedron of 14 faces close-packed around one sphere,
we find that they always compact
symmetrically and tangentially, and that this process
of enclosure may seemingly be
repeated indefinitely. Each layer, however, is in itself
a finite or complete and symmetrical
embracement of spheres. Each of these embracing layers
of spheres constitutes a finite
system. Each layer always takes the 14-face conformation
and consists of eight triangular
and six square faces. Together with the layers they
enclose and the original sphere center,
or nucleus, these symmetrically encompassing layers
constitute a concentric finite system.
If we add on more layers of equiradius spheres to
the symmetrical
polyhedron of 14 faces close-packed around one sphere,
we find that they always compact
symmetrically and tangentially, and that this process
of enclosure may seemingly be
repeated indefinitely. Each layer, however, is in itself
a finite or complete and symmetrical
embracement of spheres. Each of these embracing layers
of spheres constitutes a finite
system. Each layer always takes the 14-face conformation
and consists of eight triangular
and six square faces. Together with the layers they
enclose and the original sphere center,
or nucleus, these symmetrically encompassing layers
constitute a concentric finite system.
|

|
413.04
 As additional layers are added, it is found that a
symmetrical pattern of
concentric systems repeats itself. That is, the system
of three layers around one sphere,
with 92 spheres in the outer layer, begins all over
again and repeats itself indefinitely with
successively enclosing layers in such a way that the
successive layers outside of the 92-
sphere layer begin to penetrate the adjacent new nuclear
systems. We find then that only
the concentric system of spheres within and including
the layer of 92 are unique and
individual systems. We will pursue this concept of a
finite system in universal geometry
still further
(see Sec. 418, et seq.)
in order to relate
it to the significance of the 92 self-
regenerative chemical elements.
As additional layers are added, it is found that a
symmetrical pattern of
concentric systems repeats itself. That is, the system
of three layers around one sphere,
with 92 spheres in the outer layer, begins all over
again and repeats itself indefinitely with
successively enclosing layers in such a way that the
successive layers outside of the 92-
sphere layer begin to penetrate the adjacent new nuclear
systems. We find then that only
the concentric system of spheres within and including
the layer of 92 are unique and
individual systems. We will pursue this concept of a
finite system in universal geometry
still further
(see Sec. 418, et seq.)
in order to relate
it to the significance of the 92 self-
regenerative chemical elements.
|

|
414.00
 Nucleus
Nucleus
|

|
414.01
 In closest packing of equiradius spheres, a nucleus
by definition must be
tangentially and symmetrically surrounded. This means
that there must be a ball in every
possible tangential and optically direct angular relationship
to the nucleus. This does not
happen with the first layer of 12 balls or with the
second layer of 42 balls. Not until the
third layer of 92 balls is added are all the tangential
spaces filled and all the optically direct
angles of nuclear visibility intercepted. We then realize
a nucleus.
In closest packing of equiradius spheres, a nucleus
by definition must be
tangentially and symmetrically surrounded. This means
that there must be a ball in every
possible tangential and optically direct angular relationship
to the nucleus. This does not
happen with the first layer of 12 balls or with the
second layer of 42 balls. Not until the
third layer of 92 balls is added are all the tangential
spaces filled and all the optically direct
angles of nuclear visibility intercepted. We then realize
a nucleus.
|

|
414.02
 It will also be discovered that the third layer of
92 spheres contains eight
new potential nuclei; however, these do not become realized
nuclei until each has two
more layers enveloping it__one layer with the nucleus
in it and two layers enclosing it.
Three layers are unique to each nucleus. This tells
us that the nuclear group with 92
spheres in its outer, or third, layer is the limit of
unique, closest-packed symmetrical
assemblages of unit wavelength and frequency. These
are nuclear symmetry systems.
It will also be discovered that the third layer of
92 spheres contains eight
new potential nuclei; however, these do not become realized
nuclei until each has two
more layers enveloping it__one layer with the nucleus
in it and two layers enclosing it.
Three layers are unique to each nucleus. This tells
us that the nuclear group with 92
spheres in its outer, or third, layer is the limit of
unique, closest-packed symmetrical
assemblages of unit wavelength and frequency. These
are nuclear symmetry systems.
|

|
414.03
 It is characteristic of a nucleus that it has at least
two surrounding layers in
which there is no nucleus showing, i.e., no potential.
In the third layer, however, eight
potential nuclei show up, but they do not have their
own three unique layers to realize
them. So the new nuclei are not yet realized, they are
only potential.
It is characteristic of a nucleus that it has at least
two surrounding layers in
which there is no nucleus showing, i.e., no potential.
In the third layer, however, eight
potential nuclei show up, but they do not have their
own three unique layers to realize
them. So the new nuclei are not yet realized, they are
only potential.
|

|
414.04
 The nucleus ball is always two balls, one concave
and one convex. The two
balls have a common center. Hydrogen's one convex proton
contains its own concave
nucleus.
The nucleus ball is always two balls, one concave
and one convex. The two
balls have a common center. Hydrogen's one convex proton
contains its own concave
nucleus.
|