460.00 Jitterbug: Symmetrical Contraction of Vector Equilibrium

460.01 Definition

460.011 The "jitterbug" is the finitely closed, external vector structuring of a vector- equilibrium model constructed with 24 struts, each representing the push-pull, action-and- reaction, local compression vectors, all of them cohered tensionally to one another's ends by flexible joints that carry only tension across themselves, so that the whole system of only-locally-effective compression vectors is comprehensively cohered by omniembracing continuous four closed hexagonal cycles' tension.

460.02 When the vector-equilibrium "jitterbug" assembly of eight triangles and six squares is opened, it may be hand-held in the omnisymmetry conformation of the vector equilibrium "idealized nothingness of absolute middleness." If one of the vector equilibrium's triangles is held by both hands in the following manner__with that triangle horizontal and parallel to and above a tabletop; with one of its apexes pointed away from the holder and the balance of the jitterbug system dangling symmetrically; with the opposite and lowest triangle, opposite to the one held, just parallel to and contacting the tabletop, with one of its apexes pointed toward the individual who is handholding the jitterbug__and then the top triangle is deliberately lowered toward the triangle resting on the table without allowing either the triangle on the table or the triangle in the operator's hands to rotate (keeping hands clear of the rest of the system), the whole vector equilibrium array will be seen to be both rotating equatorially, parallel to the table but not rotating its polar-axis triangles, the top one of which the operating individual is hand- lowering, while carefully avoiding any horizontal rotation of, the top triangle in respect to which its opposite triangle, resting frictionally on the table, is also neither rotating horizontally nor moving in any direction at all.

460.03 While the equatorial rotating results from the top triangle's rotationless lowering, it will also be seen that the whole vector-equilibrium array is contracting symmetrically, that is, all of its 12 symmetrically radiated vertexes move synchronously and symmetrically toward the common volumetric center of the spherically chorded vector equilibrium. As it contracts comprehensively and always symmetrically, it goes through a series of geometricaltransformation stages. It becomes first an icosahedron and then an octahedron, with all of its vertexes approaching one another symmetrically and without twisting its axis.

460.04 At the octahedron stage of omnisymmetrical contraction, all the vectors (strut edges) are doubled together in tight parallel, with the vector equilibrium's 24 struts now producing two 12-strut-edged octahedra congruent with one another. If the top triangle of the composite octahedron (which is the triangle hand-held from the start, which had never been rotated, but only lowered with each of its three vertexes approaching exactly perpendicularly toward the table) is now rotated 60 degrees and lowered further, the whole structural system will transform swiftly into a tetrahedron with its original 24 edges now quadrupled together in the six-edge pattern of the tetrahedron, with four tetrahedra now congruent with one another. Organic chemists would describe it as a quadrivalent tetrahedral structure.

460.05 Finally, the model of the tetrahedron turns itself inside out and oscillates between inside and outside phases. It does this as three of its four triangular faces hinge open around its base triangle like a flower bud's petals opening and hinging beyond the horizontal plane closing the tetrahedron bud below the base triangle.

460.06 As the tetrahedron is opened again to the horizontal four-triangle condition, the central top triangle may again be lifted, and the whole contractive sequence of events from vector equilibrium to tetrahedron is reversed; the system expands after attaining the octahedral stage. When lifting of the topheld, nonhorizontally rotated triangle has resulted in the whole system expanding to the vector equilibrium, the equatorial rotational momentum will be seen to carry the rotation beyond dead-center, and the system starts to contract itself again. If the operating individual accommodates this momentum trend and again lowers the top triangle without rotating it horizontally, the rotation will reverse its original direction and the system will contract through its previous stages but with a new mix of doubled-up struts. As the lowering and raising of the top triangle is continuously in synchronization with the rotatingcontracting-expanding, the rotation changes at the vector equilibrium's "zero"__this occasions the name jitterbug. The vector equilibrium has four axial pairs of its eight triangular faces, and at each pair, there are different mixes of the same struts.

460.07 The jitterbug employs only the external vectors of the vector equilibrium and not its 12 internal radii. They were removed as a consequence of observing the structural stability of 12 spheres closest packed around a nuclear sphere. When the nuclear sphere is removed or mildly contracted, the 12 balls rearrange themselves (always retaining their symmetry) in the form of the icosahedron. Removal of the radial vectors permitted contraction of the model__and its own omnisymmetrical pulsation when the lowering and raising patterns are swiftly repeated. It will be seen that the squares accommodate the jitterbug contractions by transforming first into two equiangular triangles and then disappearing altogether. The triangles do not change through the transformation in size or angularity. The original eight triangles of the vector equilibrium are those of the octahedron stage, and they double together to form the four faces of the tetrahedron.

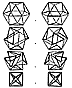Fig. 460.08

460.08 In the jitterbug, we have a sizeless, nuclear, omnidirectionally pulsing model. The vector-equilibrium jitterbug is a conceptual system independent of size, ergo cosmically generalizable. (See Secs.515.10 and 515.11.)

461.00 Recapitulation: Polyhedral Progression in Jitterbug

461.01 If the vector equilibrium is constructed with circumferential vectors only and joined with flexible connectors, it will contract symmetrically, due to the instability of the square faces. This contraction is identical to the contraction of the concentric sphere packing when the nuclear sphere is removed. The squares behave as any four balls will do in a plane. They would like to rest and become a diamond, to get into two triangles. They took up more room as a square, and closer packing calls for a diamond. The 12 vertexes of the vector equilibrium simply rotate and compact a little. The center ball was keeping them from closer packing, so there is a little more compactibility when the center ball goes out.

461.02 Icosahedron: The icosahedron occurs when the square faces are no longer squares but have become diamonds. The diagonal of the square is considerably longer than its edges. But as we rotate the ridge pole, the diamonds become the same length as the edge of the square (or, the same length as the edge of the tetrahedron or the edge of the octahedron). It becomes the octahedron when all 30 edges are the same length. There are no more squares. We have a condition of omnitriangulation.

461.03 We discover that an icosahedron is the first degree of contraction of the vector equilibrium. We never catch the vector equilibrium in its true existence in reality: it is always going one way or the other. When we go to the icosahedron, we get to great realities. In the icosahedron, we get to a very prominent fiveness: around every vertex you can always count five.

461.04 The icosahedron contracts to a radius less than the radii of the vector equilibrium from which it derived. There is a sphere that is tangent to the other 12 spheres at the center of an icosahedron, but that sphere is inherently smaller. Its radius is less than the spheres in tangency which generate the 12 vertexes of the vector equilibrium or icosahedron. Since it is no longer the same-size sphere, it is not in the same frequency or in the same energetic dimensioning. The two structures are so intimate, but they do not have the same amount of energy. For instance, in relation to the tetrahedron as unity, the volume of the icosahedron is 18.51 in respect to the vector equilibrium's volume of 20. The ratio is tantalizing because the mass of the electron in respect to the mass of the neutron is one over 18.51. That there should be such an important kind of seemingly irrational number provides a strong contrast to all the other rational data of the tetrahedron as unity, the octahedron as four, the vector equilibrium as 20, and the rhombic dodecahedron as six: beautiful whole rational numbers.

461.05 The icosahedron goes out of rational tunability due to its radius being too little to permit it having the same-size nuclear sphere, therefore putting it in a different frequency system. So when we get into atoms, we are dealing in each atom having its unique frequencies.

461.06 In the symmetrical jitterbug contraction, the top triangle does not rotate. Its vertex always points toward the mid-edge of the opposite triangle directly below it. As the sequence progresses, the top triangle approaches the lower as a result of the system's contraction. The equator of the system twists and transforms, while the opposite triangles always approach each other rotationlessly. They are the polar group.

461.07 Octahedron: When the jitterbug progresses to the point where the vector edges have doubled up, we arrive at the octahedron. At this stage, the top triangle can be pumped up and down with the equatorial vectors being rotated first one way and then the other. There is a momentum of spin that throws a twist into the system__positive and negative. The right-hand octahedron and the left-hand octahedron are not the same: if we were to color the vectors to identify them, you would see that there are really two different octahedra.

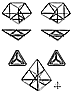Fig. 461.08

461.08 Tetrahedron: As the top triangle still plunges toward the opposite triangle, the two corners, by inertia, simply fold up. It has become the tetrahedron. In the octahedron stage, the vectors were doubled up, but now they have all become fourfold, or quadrivalent. The eight tetrahedra of the original vector equilibrium are now all composited as one. They could not escape from each other. We started off with one energy action in the system, but we have gone from a volume of 20 to a volume of one.7 The finite closure of the four-great-circle, six-hexagon-vector "necklaces" were never "opened" or unfastened.

(Footnote 7: In vectorial geometry, you have to watch for the times when things double up. The vectors represent a mass and a velocity. Sometimes they double up so they represent twice the value__when they become congruent.)

461.09 We have arrived at the tetrahedron as a straight precessional result. The quadrivalent tetrahedron is the limit case of contraction that unfolds and expands again symmetrically only to contract once more to become the other tetrahedron (like the pumping of the positive and negative octahedron). All of the jitterbug sequence was accomplished within the original domain of the vector equilibrium. The tensional integrity survives within the internal affairs domain of atoms.

461.10 Deceptiveness of Topology: Quanta Loss By Congruence: (See poster, color plate 4.) The vector equilibrium jitterbug provides the articulative model for demonstrating the always omnisymmetrical, divergently expanding or convergently contracting intertransformability of the entire primitive polyhedral hierarchy, structuring- as-you-go, in an omnitriangularly oriented evolution.

461.11 As we explore the interbonding (valencing) of the evolving structural components, we soon discover that the universal interjoining of systems__and their foldabilitypermit their angularly hinged convergence into congruence of vertexes(single- bonding), or congruence of vectors (doublebonding), or congruence of faces (triple- bonding), or volumetric congruence (quadrivalent), but each of the multicongruences appears as only one vertex or one edge or one face aspect. The Eulerean topological accounting as presently practiced__ innocent of the inherent synergetical hierarchy of intertransformability__ accounts each of these multicongruent topological aspects as consisting of only one such aspect. This misaccounting has prevented the physicists and chemists from conceptual identification of their data with synergetics' disclosure of nature's comprehensively rational intercoordinate mathematical system.

461.12 Only the topological analysis of synergetics can account for all the multicongruent__ two-, three-, fourfold__ topological aspects by accounting for the initial tetravolume inventories of the comprehensive rhombic dodecahedron and the vector equilibrium. The rhombic dodecahedron has an initial tetravolume of 48, and the vector equilibrium has an inherent tetravolume of 20. Their respective initial or primitive inventories of vertexes, vectors, and faces are always present (though often imperceptibly so) at all stages in nature's comprehensive 481 convergence transformation.

461.13 Although superficially the tetrahedron seems to have only six vectors, we witness in the jitterbug transformation that it has in fact 24. (See poster 4 and Fig. 461.08) The sizeless, primitive tetrahedron__conceptual independent of size__is quadrivalent, inherently having eight potential alternate ways of turning itself inside out: four passive and four active, meaning that four positive and four negative tetrahedra are congruent.

461.14 Only by recognizing the deceptiveness of Eulerean topology can synergetics account for the primitive total inventories of all aspects and thus conceptually demonstrate and prove the validity of Boltzmann's concepts as well as those of all quantum phenomena. Synergetics mathematical accounting conceptually interlinks the operational data of physics and chemistry and their complex associabilities manifest in such disciplines as geology, biology, and others.