920.00 Functions of A and B Modules

920.01 The A and B Quanta Modules may possibly quantize our total experience. It is a phenomenal matter to discover asymmetrical polyhedral units of geometry that are reorientably compositable to occupy one asymmetrical polyhedral space; it is equally unique that, despite disparate asymmetric polyhedral form, both have the same volume; and both associate in different kinds of simplex and complex, symmetrical and asymmetrical, coherent systems. While they consist, in their positive and negative aspects, of four different asymmetrical shapes, their unit volume and energy quanta values provide a geometry elucidating both fundamental structuring and fundamental and complex intertransformings, both gravitational and radiational.
921.00 Energy Deployment in A and B Quanta Modules
921.01 By virtue of their properties as described in Secs. 920, 921.20 , and 921.30 , the centers of energy in the A and B Quanta Modules can be locally reoriented within the same space without disturbing contiguously surrounding configurations of closest-packed geometry; these local reorientations can either concentrate and hold or deploy and distribute the energies of the respective A and B Quanta Modules, in the first case concentrating the centers of energy inwardly, and in the second case deploying the centers of energy outwardly.
921.02 In X-ray diffraction, you can see just such alternate energy concentrations of omnideployed patterns in successive heat treatments of metals. You can hit a piece of metal and you will find by X-ray diffraction that a previously concentrated array of centers of energy have been elegantly deployed. When you take the temper out of the metal, the energy centers will again change their positions. The metal's coherence strength is lessened as the energy centers are outwardly deployed into diffused remoteness from one another. When the centers of energy are arranged closer to one another, they either attract or repulse one another at the exponentially increasing rates of gravitational and radiational law. When we heat-treat or anneal metals and alloys, they transform in correspondence with the reorientabilities of the A and B Quanta Modules.
921.03 The identical volumes and the uniquely different energy-transforming capabilities of the A and B Quanta Modules and their mathematically describable behaviors (10F2 + 2) hint at correspondence with the behaviors of neutrons and protons. They are not mirror images of one another, yet, like the proton and neutron, they are energetically intertransformable and, due to difference of interpatternability, they have difference in mass relationship. Whether they tend to conserve or dissipate energy might impose a behavioral difference in the processes of measuring their respective masses. A behavioral proclivity must impose effects upon the measuring process.
921.04 The exact energy-volume relationship of the A and B Quanta Modules and their probable volumetric equivalence with the only meager dimensional transformations of the 120 LCD tetrahedral voids of the icosahedron (see Sec. 905.60) may prove to have important physical behavior kinships.
921.10 Energy Behavior in Tetrahedra: A tetrahedron that can be folded out of a single foldable triangle has the strange property of holding energy in varying degrees. Energy will bounce around inside the tetrahedron's four internal triangles as we described its bouncing within one triangle (see Sec. 901). Many bounce patterns are cyclically accomplished without tendency to bounce out of tetrahedrons, whether regular or irregular, symmetrical or asymmetrical.
921.11 The equiangled, omni-sixty-degreed, regular tetrahedron can be opened along any three edges converging at any one of its vertexes with its edge-separated vertexial group of three triangles appearing as a three-petaled flower bud about to open. By deliberately opening the three triangular petals, by rotating them outward from one another around their three unsevered base-edge hinges, all three may be laid out flat around the central base triangle to appear as a two-frequency, edge-moduled, equiangular triangle consisting of four internal triangles. Energy tends by geodesical economy and angular law to be bounce-confined by the tetrahedron.
921.12 The irregular, asymmetrical, tetrahedral A Quanta Module's four triangular facets unfold spirally into one asymmetrical triangle.
921.13 But the triangular facets of the B Quanta Module unfold inherently into four mutually dissimilar but interhinged 90-degree triangles.
921.14 All the interior edges of the triangles, like the edges of a triangular billiard table, will provide unique internal, bouncing, comer-pocket-seeking patterns. An equilateral, equiangled triangle will hold the bouncing with the least tendency to exit at the pocketed comers. The more asymmetrical the triangular billiard table, the more swiftly the angular progression to exit it at a comer pocket. The various bounce patterns prior to exit induce time-differentiated lags in the rate of energy release from one tetrahedron into the other tetrahedron.
921.15 Energy bounces around in triangles working toward the narrowest vertex, where the impossibility of more than one line going through any one point at any one time imposes a twist vertex exit at the comers of all polyhedra. Therefore, all triangles and tetrahedra "leak" energy, but when doing so between two similar corresponding vertexes- interconnected tetrahedra, the leaks from one become the filling of the other.
921.20 Energy Characteristics of A Quanta Module: The A Quanta Modules can hold energy and tend to conserve it. They do so by combining with one another in three unique ways, each of which combine as one regular tetrahedron; the regular tetrahedron being a fundamental energy-holding form-the energy being held bounce-describing the internal octahedron of every tetrahedron.
921.21 The A Quanta Modules can also combine with the B Quanta Modules in seven ways, each of which result in single whole tetrahedra, which, as noted, hold their energy within their inherent octahedral centers.
921.30 Energy Characteristics of B Quanta Module: The B Quanta Modules can vertex-combinedly hold energy but tend to release it.
921.31 While all the single triangles will hold swift-motion energies only for relatively short periods of time, the four very asymmetrical and dissimilar triangles of the B Quanta Module will release energy four times faster than any one of their asymmetrical tetrahedral kin.
921.32 The B Quanta Modules do not retain energy, and they cannot combine with one another to form a single tetrahedron with energy-introverting and -conserving proclivities.
921.40 Summary: Though of equal energy potential or latent content, the As and the Bs are two different systems of unique energy-behavior containment. One is circumferentially embracing, energy-impounding, integratively finite, and nucleation- conserving. The other is definitively disintegrative and nuclearly exportive. A is outside- inwardly introvertive. B is outside-outwardly extrovertive. (See Illus. 924.20.)
922.00 Conceptual Description and Contrast
922.01 The A Quanta Module is all of the nonconsidered, nonconceptual, finite, equilibrious, not-now-tuned-in Universe.
922.02 The B Quanta Module is the only momentarily extant considered subdivision of disequilibrious Universe, i.e., the attention-preoccupying, special-case local system. The B Quanta Module is always the real live "baby"; it is most asymmetrical.
923.00 Constant Volume

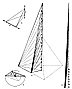Fig. 923.10 		923.10 Precession of Two Module Edges: There are six edges of a tetrahedron, and each edge precesses the opposite edge toward a 90-degrees-maximum of attitudinal difference of orientation. Any two discrete, opposite edges can be represented by two aluminum tubes, X and Y (see Illus. 923.10D), which can move longitudinally anywhere along their respective axes while the volume of the irregular tetrahedra remains constant. They may shuttle along on these lines and produce all kinds of asymmetrical tetrahedra, whose volumes will always remain unit by virtue of their developed tetrahedra's constant base areas and identical altitudes. The two tubes' four ends produce the other four interconnecting edges of the tetrahedron, which vary as required without altering the constantly uniform volume.
923.15 One Tetra Edge Constant: Using a constant-volume, vectorially edged tetrahedron ABCD with six edges AB, AC, AD, BC, BD, and CD, and with only one of those six edge lengths holding a constant length AB, all five of the tetrahedron's other edge lengths may covary as the tetrahedron rotates around the fixed edge length AB, which acts as an axis of rotation. While the axis AB is precessionally tilted within its celestial theater, it is experientially demonstrable that__without changing the tetrahedron's volume or its constant-length vector AB__its two other corners C and D may interconnect the AB-fixed-length-axis points with any other two points in Universe no matter how remote from one another. This is the reason why electromagnetic waves can interlink any points in Universe in response to a given constant wavelength AB. (Compare Secs. 426.40, 530.11 , 960.08 , and 961.10-40.)
923.20 Constant Volume: A comparison of the end views of the A and B Quanta Modules shows that they have equal volumes as a result of their equal base areas and identical altitudes. (See Sec. 621.)
923.21 A line can be projected from its origin at the center of area of the triangular base of a regular tetrahedron, outward through the opposite apex of the tetrahedron to any desired distance. When subdivided into increments equal to the distance between its triangular-base center and its apex, and when each of these equilinear increments outward beyond the apex is interconnected by three lines leading to each of the three comers of the base triangle, then each of the successive volumetric additions will be of identical volume to that of the original tetrahedra, and the overall form will be that of a tetrahedron which become progressively longer and sharp-pointed with each addition. (See Illus. 923.10 A, B, and C.) As the ever-sharpening and elongating tetrahedron approaches infinity, the three elongating edges tend to parallelism; i.e., toward what is known as parallax in astronomy. The modules will tend to congruence with the parallaxing lines. Each full-line- long length model of these congruent lines will have the same volume as the original module.
923.30 Energy Accommodation: The A and B Quanta Modules start with unit base and add unit altitude, C, D, E, F, and so forth, but as each additional altitude is superimposed, the volume remains the same: a volume of one. We find these linear incrementation assemblies getting longer, with their additional volumes always one. Suppose we think about this progression as forming an electric-wire conductor and divide its circular base into three 120-degree angles. Its progressive conic increments could grow and operate in the same manner as our constant-volume, tetrahedral modules.
923.31 We will inherently superimpose progressive base-to-apex attenuating sections. In the electric conductor wire, this means that whatever energy increment is fed into the first base module will tend to be conducted at various unit frequencies along the line. Each unique frequency introduced at the base will create its unique conic altitude incrementation. The outermost, line-long cone's energy quantum will always be the same as that of the initial base cone. Finally, the last and outermost cone is just as long as the wire itself-so there is an outside charge on the wire tending to fluoresce a precessional broadcasting of the initial inputs at 90 degrees; i.e., perpendicularly away from the wire. This may elucidate antenna behaviors as well as long-distance, high-voltage, electric energy conductions which tend to broadcast their conducted energy. (For further elaboration of the constant-volume, tetrahedral models, see Secs. 961.10, 961.20, 961.30 and 961.40.)
924.00 Congruence of Centers
924.10 Congruence of A and B Quanta Module Centers: Within either the A or B Quanta Modules the
centers of effort;
centers of energy;
centers of gravity;
centers of radiation;
centers of volume; and
centers of field
are congruent, i.e., identical. The same centers are involved. We will call their six congruent centers their synergetic centers.
924.11 But the A (+) and A (-), and B (+) and B (-) respective volumetric centers are never congruent. However, the positive or the negative AAB aggregates (these are the "Mites." See Sec. 953.10) have identical volumetric centers.

Table 924.20 		924.20 Table of Tetrahedral Functions of A and B Quanta Modules
Next Section: 930.00
Copyright © 1997 Estate of R. Buckminster Fuller