Table 943.00
Fig. 943.00A
Fig. 943.00B
Table: Synergetics Quanta Module Hierarchy
|
Table 943.00 Fig. 943.00A Fig. 943.00B |
943.00
Table: Synergetics Quanta Module Hierarchy
|
|
943.01
The orderly elegance of progressive numbers of concentric
shells, starting
with one as a discrete arithmetical progression, as
well as the pattern of energy quanta
modules growth rate, and their respective layer-transformation
pairings of positive and
negative arrangements of A and B Quanta Modules, of
which there are always an even
number of (+) or (-) As or Bs, is revealed in the synergetic
quanta module hierarchy of
topological characteristics.
|
950.00
Allspace Filling
|
|
950.01
The regular tetrahedron will not associate with other
regular tetrahedra to fill
allspace. (See Sec.
780.10
for a conceptual definition
of allspace.) If we try to fill allspace
with tetrahedra, we are frustrated because the tetrahedron
will not fill all the voids above
the triangular-based grid pattern. (See Illus.
950.31.)
If we take an equilateral triangle and
bisect its edges and interconnect the mid-points, we
will have a "chessboard" of four
equiangular triangles. If we then put three tetrahedra
chessmen on the three corner
triangles of the original triangle, and put a fourth
tetrahedron chessman in the center
triangle, we find that there is not enough room for
other regular tetrahedra to be inserted
in the too-steep valleys Lying between the peaks of
the tetrahedra.
|
|
|
950.02
If we remove the one tetrahedral chessman from the
center triangle of the
four-triangle chessboard and leave the three tetra-chessmen
standing on the three corner
triangles, we will find that one octahedral chessman
(of edges equal to the tetra) exactly
fits into the valley Lying between the first three tetrahedra;
but this is not allspace-filling
exclusively with tetrahedra.
|
|
|
950.10
Self-Packing Allspace-Filling Geometries
|
|
|
950.11
There are a variety of self-packing allspace-filling
geometries. Any one of
them can be amplified upon in unlimited degree by highfrequency
permitted aberrations.
For instance, the cube can reoccur in high frequency
multiples with fundamental rectilinear
aspects_with a cubical node on the positive face and
a corresponding cubical void dimple
on the negative face_which will fill allspace simply
because it is a complex of cubes.
|
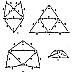 Fig. 950.12 |
950.12
There are eight familiar self-packing allspace-fillers:
|
|
|
950.20
Cubical Coordination
|
|
|
950.21
Because the cube is the basic, prime-number-three-elucidating
volume, and
because the cube's prime volume is three, if we assess
space volumetrically in terms of the
cube as volumetric unity, we will exploit three times
as much space as would be required
by the tetrahedron employed as volumetric unity. Employing
the extreme, minimum, limit
case, ergo the prime structural system of Universe,
the tetrahedron (see Sec.
610.20), as
prime measure of efficiency in allspace filling, the
arithmetical-geometrical volume
assessment of relative space occupancy of the whole
hierarchy of geometrical phenomena
evaluated in terms of cubes is threefold inefficient,
for we are always dealing with physical
experience and structural systems whose edges consist
of events whose actions, reactions,
and resultants comprise one basic energy vector. The
cube, therefore, requires threefold
the energy to structure it as compared with the tetrahedron.
We thus understand why
nature uses the tetrahedron as the prime unit of energy,
as its energy quantum, because it
is three times as efficient in every energetic aspect
as its nearest symmetrical, volumetric
competitor, the cube. All the physicists' experiments
show that nature always employs the
most energy-economical strategies.
|
|
|
950.30
Tetrahedron and Octahedron as Complementary Allspace
Fillers: A
and B Quanta Modules
|
|
|
950.31
We may ask: What can we do to negotiate allspace filling
with tetrahedra? In
an isotropic vector matrix, it will be discovered that
there are only two polyhedra
described internally by the configuration of the interacting
lines: the regular tetrahedron
and the regular octahedron. (See Illus.
950.31.)
|
|
|
950.32
All the other regular symmetric polyhedra known are
also describable
repetitiously by compounding rational fraction elements
of the tetrahedron and
octahedron: the A and B Quanta Modules, each having
the volume of 1/24th of a
tetrahedron.
|
|
|
950.33
It will be discovered also that all the polygons formed
by the interacting
vectors consist entirely of equilateral triangles and
squares, the latter occurring as the
cross sections of the octahedra, and the triangles occurring
as the external facets of both
the tetrahedra and octahedra.
|
|
|
950.34
The tetrahedra and octahedra complement one another
as space fillers. This
is not very satisfactory if you are looking for a monological
explanation: the "building
block" of the Universe, the "key," the ego's wished-for
monopolizer. But if you are
willing to go along with the physicists, recognizing
complementarity, then you will see that
tetrahedra plus octahedra_and their common constituents,
the unit-volume, A and B
Quanta Modules_provide a satisfactory way for both physical
and metaphysical,
generalized cosmic accounting of all human experience.
Everything comes out rationally.
|
| Next Section: 951.00 |