609.00 Instability of Polyhedra from Polygons of More Than Three Sides

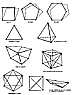Fig. 609.01 		609.01 Any polygon with more than three sides is unstable. Only the triangle is inherently stable. Any polyhedron bounded by polygonal faces with more than three sides is unstable. Only polyhedra bounded by triangular faces are inherently stable.

610.00 Triangulation

610.01 By structure, we mean a self-stabilizing pattern. The triangle is the only self- stabilizing polygon.
610.02 By structure, we mean omnitriangulated. The triangle is the only structure. Unless it is self-regeneratively stabilized, it is not a structure.
610.03 Everything that you have ever recognized in Universe as a pattern is re- cognited as the same pattern you have seen before. Because only the triangle persists as a constant pattern, any recognized patterns are inherently recognizable only by virtue of their triangularly structured pattern integrities. Recognition is as dependent on triangulation as is original cognition. Only triangularly structured patterns are regenerative patterns. Triangular structuring is a pattern integrity itself. This is what we mean by structure.
610.10 Structural Functions
610.11 Triangulation is fundamental to structure, but it takes a plurality of positive and negative behaviors to make a structure. For example:
__always and only coexisting push and pull (compression and tension);
__always and only coexisting concave and convex;
__always and only coexisting angles and edges;
__always and only coexisting torque and countertorque;
__always and only coexisting insideness and outsideness;
__always and only coexisting axial rotation poles;
__always and only coexisting conceptuality and nonconceptuality;
__always and only coexisting temporal experience and eternal conceptuality.
610.12 If we want to have a structure, we have to have triangles. To have a structural system requires a minimum of four triangles. The tetrahedron is the simplest structure.
610.13 Every triangle has two faces: obverse and reverse. Every structural system has omni-intertriangulated division of Universe into insideness and outsideness.

Fig. 610.20 		610.20 Omnitriangular Symmetry: Three Prime Structural Systems
610.21 There are three types of omnitriangular, symmetrical structural systems. We can have three triangles around each vertex; a tetrahedron. Or we can have four triangles around each vertex; the octahedron. Finally we can have five triangles around each vertex; the icosahedron. (See Secs. 532.40, 610.20, 724, 1010.20, 1011.30 and 1031.13.)
610.22 The tetrahedron, octahedron, and icosahedron are made up, respectively, of one, two, and five pairs of positively and negatively functioning open triangles.
610.23 We cannot have six symmetrical or equiangular triangles around each vertex because the angles add up to 360 degrees-thus forming an infinite edgeless plane. The system with six equiangular triangles "flat out" around each vertex never comes back upon itself. It can have no withinness or withoutness. It cannot be constructed with pairs of positively and negatively functioning open triangles. In order to have a system, it must return upon itself in all directions.
610.24 Limit Cases: Macro, Medio, and Micro: Considered geometrically, triangles are the only self-stabilizing polygonal patterns__ergo, only triangles are structurally stable. Since we cannot construct a polyhedral system of only two triangles around each corner (because a polyhedral system must by definition have an insideness and an outsideness in order definitively and closingly to separate the Universe into macrocosm and microcosm), and since we cannot have six equilateral triangles around each vertex of a polyhedral system (for each of the six would themselves separate out from the others to form flat planes and could not close back to join one another to separate Universe definitively into macrocosm and microcosm)__ergo, the tetrahedron, octahedron, and icosahedron constitute the minimum, middle, and maximum cases of omnitriangulated__ergo, stabilized__structural subdividings of Universe into macro, medio, and micro Universe divisions.
610.30 Structural Harmonics
610.31 The conceptual sequence in the left column of Fig. 610.20 illustrates the basic octave behavior of structural transformations. The first three figures__tetra, octa, icosa__represent the positive outside-out set of primitive structural systems. Three equiangular triangles around each corner add to tetra; four around each corner add to octa; five around each corner add to icosa; but six 60-degree angles around each corner add to 360 degrees; ergo, produce an infinitely extendible plane; ergo, fail to return upon themselves embracingly to produce a system's insideness and outsideness; ergo, thus act as the zerophase of maximum evolution changing to the involution phase of maximum nothingness. As the transformation sequence changes from divergent evolution to convergent involution, from five, then four, then three equiangular triangles around each corner, it thereby produces successively the inside-out icosa, octa, and tetra, until the convergent involutional contraction attains the phase of maximum nothingness. At the minimum zero bottom of the sequence the inside-out tetra revolves outside-out to minimum somethingness of tetravolume I as the transformation diverges expansively to the maximum vector-equilibrium somethingness of tetravolume 20, thereafter attaining maximum nothingness and evolution-to-involution conversion. (See Sec. 1033.)
610.32 At six-vector hexagonality we have the vector equilibrium at maximum zero evolution-to-involution conversion.
610.33 The minimum zero tetrahedron with which the series commences repeats itself beneath the bottom figure to permit the accomplishment of octave harmony at minimum zero conversion whose terminal nothingnesses accommodate the overlapping interlinkages of the octave terminals: thus do-remi-fa-solla-ti do.
611.00 Structural Quanta
611.01 If the system's openings are all triangulated, it is structured with minimum effort. There are only three possible omnisymmetrical, omnitriangulated, least-effort structural systems in nature. They are the tetrahedron, octahedron, and icosahedron. When their edges are all equal in length, the volumes of these three structures are, respectively, one, requiring one structural quantum; four, requiring two structural quanta; and 18.51, requiring five structural quanta. Six edge vectors equal one minimum-structural system: 6 edge vectors = 1 structural quantum.
611.02 Six edge vectors = one tetrahedron. One tetrahedron=one structural quantum.
1 Tetrahedron (volume 1) = 6 edge vectors = 1 structural quantum;
1 Octahedron (volume 4) = 12 edge vectors = 2 structural quanta;
1 Icosahedron (volume 18.51) =30 edge vectors =5 structural quanta.
Therefore:
with tetrahedron, 1 structural quantum provides 1 unit of volume;
with octahedron, 1 structural quantum provides 2 units of volume;
with icosahedron, 1 structural quantum provides 3.7 units of volume.
612.00 ubtriangulation: Icosahedron
612.01 Of the three fundamental structures, the tetrahedron contains the most surface and the most structural quanta per volume; it is therefore the strongest structure per unit of volume. On the other hand, the icosahedron provides the most volume with the least surface and least structural quanta per units of volume and, though least strong, it is structurally stable and gives therefore the most efficient volume per units of invested structural quanta.
612.10 Units of Environment Control: The tetrahedron gives one unit of environment control per structural quantum. The octahedron gives two units of environment control per structural quantum. The icosahedron gives 3.7 units of environment control per structural quantum.

Fig. 612.11 		612.11 That is the reason for the employment of the triangulated icosahedron as the most efficient fundamental volume-controlling device of nature. This is the way I developed the multifrequency-modulated icosahedron and geodesic structuring. This is probably the same reason that nature used the multifrequency-modulated icosahedron for the protein shells of the viruses to house most efficiently and safely all the DNA-RNA genetic code design control of all biological species development. I decided also to obtain high local strength on the icosahedron by subtriangulating its 20 basic Icosa LCD spherical triangles with locally superimposed tetrahedra, i.e., an octahedron-tetrahedron truss, which would take highly concentrated local loads or impacts with minimum effort while the surrounding rings of triangles would swiftly distribute and diminishingly inhibit the outward waves of stress from the point of concentrated loading. I had also discovered the foregoing structural mathematics of structural quanta topology and reduced it to demonstrated geodesic dome practice before the virologists discovered that the viruses were using geodesic spheres for their protein shell structuring. (See Sec. 901.)
Next Section: 613.00
Copyright © 1997 Estate of R. Buckminster Fuller