955.50 Rhombic Dodecahedron at Heart of Vector Equilibrium: Nature always starts every ever freshly with the equilibrious isotropic-vector-matrix field. Energy is not lost; it is just not yet realized. It can be realized only disequilibriously.
955.51 At the heart of the vector equilibrium is the ball in the center of the rhombic dodecahedron.

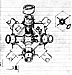Fig. 955.52 		955.52 Look at the picture which shows one-half of the rhombic dodecahedron. (See Illus. 955.52.) Of all the polyhedra, nothing falls so readily into a closest-packed group of its own kind as does the rhombic dodecahedron, the most common polyhedron found in nature.

960.00 Powers and Dimensions

960.01 The Coordination of Number Powers and Geometrical Dimensions
960.02 Powering means the multiplication of a number by itself.
960.03 Number powers refer to the numbers of times any given number is multiplied by itself. While empty set numbers may be theorized as multipliable by themselves, so long as there is time to do so, all experimental demonstrability of science is inherently time limited. Time is size and size is time. Time is the only dimension. In synergetics time-size is expressible as frequency.
960.04 Recalling our discovery that angles, tetrahedra, and topological characteristics are system constants independent of size, the limit of experimentally demonstrable powering involves a constant vector equilibrium and an isotropic vector matrix whose omnisymmetrically interparalleled planes and electable omniuniform frequency reoccurrences accommodate in time-sizing everywhere and anywhere regenerative (symmetrically indestruct, tetrahedral, four-dimensional, zerophase, i.e., the vector equilibrium) rebirths of a constant, unit-angle, structural system of convergent gravitation and divergent radiation resonatability, whose developed frequencies are the specific, special-case, time-size dimensionings.
960.05 Dimensional growth is not occasioned by an increase in exponential powers. It is brought about by increasing subdivision of the constant whole of Universe to isolate a locally considerable increment. For instance, E = Mc2 says that the amount of energy involved in the isolated "mass" as a local event complex of Universe under consideration in this particular instance is to be determined by reference to the constant amount of cosmic energy involved in the constant rate of growth of a spherical, electromagnetic, wave surface, which constant is c2. Because the potential energy is in vector equilibrium packages, the centers of energy rebirth are accommodated by the isotropic vector matrix. The constant power is the frequency 10F2 + 2, which accommodates all the exportive- importive, entropic-syntropic, regeneration patterning of Universe.
960.06 The only dimension is time, the time dimension being the radial dimension outward from or inward toward any regenerative center, which may always be anywhere, yet characterized by always being at the center of system regeneration.
960.07 The time dimension is frequency.
960.08 Any point can tune in any other point in Universe. All that is necessary is that they both employ the same frequency, the same resonance, the same system, center to center.
960.09 The total nothingness involved is accounted by 20F3. The third power accounts both the untuned nothingness and the finitely tuned somethingness. The 20 is both Einstein's empty set M and all the other untuned non-M of Universe. The 20F3 is the total Universe momentarily all at one time or timeless center. Eternity is 1 = No frequency 13 = 1 × 20. The 20 is eternally constant. The rate of wave growth corresponding to Einstein's c2 = 10F2 + 2.
960.10 Thus the isotropic vector matrix of synergetics' convergence and divergence accommodates elegantly and exactly both Einstein's and Newton's radiation and gravitation formulations, both of which are adequately accounted only in second-powered terms.
960.11 Distance is time. Distance is only frequency-accountable.
960.12 Newton's intermass attraction increases at the second power as the time- distance between is halved. Newton and Einstein deal only with mass and frequency to the second power. Their masses are relatively variable. In one, mass is acceleratingly expended; in the other, mass is acceleratingly collected. (See Sec. 1052.21.)
960.13 In synergetics, the total mass somethingness to be acceleratingly expended is 10F2, with always a bonus spin-aroundable-polar-axis 2: Me and the Otherness. In synergetics, the total nothingness and somethingness involved in both inbound and outbound field is 20F3. (Nothing = 10. Something = 10. Both = 20.) The multiplicative twoness of me and the otherness. The vector equilibrium and the icosahedron are the prime number five polyhedra; the multiplicative, concave-convex twoness: 2 × 5 = 10. F3 = Unexpected nothingness F1 × Expected somethingness F2 = F3.
961.00 Unitary Quantation of Tetrahedron
961.01 The area of a triangle is arrived at by multiplying the length of the baseline by one-half of the triangle's apex altitude.
961.02 The volume of a tetrahedron is the product of the area of the base and one- third of its altitude.
961.03 A minimum garland of "granteds" combines only synergetically to disclose the following:
961.10 Granted: A Slidable Model of Constant Volume: Granted any point A that is movable limitlessly anywhere within one of two planes parallel to one another at a given perpendicular distance X from one another, and, cogliding anywhere within the other parallel plane, two parallel lines lying at a given perpendicular distance Y from one another, and a point B that is slidable anywhere along one of the parallel lines, along the other line of which (two parallel lines) is a slidable pair of points, C and D, always slidable only at a constant and given distance Z from one another; it will be found that the vast variety of tetrahedra to be formed by interconnecting these four points (two independently variable and two only covariable) will always enclose the same volume. (See Sec. 923 and Illus. 923.10D.)
961.11 Provided the relationship between X, Y, and Z remain constant as described, and the distances X and Y in respect to the "constructed" distance are always such that
Y = sqrt(Z2 - (1/2 × Z)2)
and
X = sqrt(Z2 - (2/3 × Y)2)
then, by varying Z to correspond with the distance between two experiential event foci, all the other vertexial positions of all the tetrahedra of equal volume can be described by revolution of the constantly cohered tetrahedral system around the axial line running through the two points C and D. This axial line may itself be angularly reoriented to aim the tetrahedral system by combining and interconnecting circuitry closing in any direction, thereby to reach any other two points in Universe to be tetrahedrally interjoined in unitary quantation.
961.12 With the observer-articulator's experientially initiated and interpositioned two control points C and D, these uniformly quantated observer-articulator variable initial "tunings," accomplished exclusively by frequency and angle modulations, may "bring in" subjectively-objectively, receivingly-and-transmittingly, omnicosmic events occurring remotely in nonsimultaneously evolving and only otherness-generated self-awareness and deliberately thinkable self-conceptioning of progressively omnicomprehending embracements and penetrations. This in turn enables the conscious designing capabilities to be realized by these omnicosmic reaching tetrahedral coordinations (which are resolvable into generalized, quantum-regularized sets, consisting of only two human individual mentalities' predeterminable variables consisting exclusively of frequency and angle modulations identified only with the self-and-other, C- and D-defined, selectable wavelength Z and the Z axis' angular aiming and reorientation regulatability of the Z axis' ever-constant reorientations of its X- and Y-dependent coordinates in exclusively angle- and frequency-determined invariant relationship), all of whose synergetic integrities' intersignificance realizations are eternally interaccommodated by the tetrahedral structural system's prime conceptual initiations.
961.20 Granted: A Model of Comprehensive Covariability: Granted that a tetrahedron of given altitude X, with a base triangle of given altitude Y and given baseline edge length Z, is volumetrically constant independent of the omnivariable interangling of its four vertexes, and five variable-length edges, and four variable triangular faces, whose comprehensive covariability can altogether accommodate any symmetric or asymmetric aspect transformability to correspond exactly in all its interangular face relationships and relative edge lengths with any tetrahedron to be formed by interconnecting any four points in Universe, provided the relative values of X and Y in respect to Z (which is the only experientially known distance) are always such that:
Y = sqrt(Z2 - (1/2 × Z)2)
and,
X = sqrt(Z2 - (2/3 × Y)2)
As the values only of Z are altered, the respective value of the uniformly volumed tetrahedra will vary at a rate of the third power of Z's linear change.
961.30 Granted: A Model for Third-Power Rate of Variation: Granted that there is then in respect to any two points in Universe a tetrahedron that can be given any symmetrical or asymmetrical tetrahedral shape, any of whose volumes will remain uniform or will vary uniformly at a third-power rate in respect to any alteration of the distance between the two initial control points on the axial control line; then, any four points in Universe, provided one is not in the plane of the other three, can be interconnected by varying the angular orientation of the control-line axis and the distance between the two central control points.
961.31 Being generalized, these three relative distance-control coordinates X, Y, and Z are, of course, also present in the special-case, omnirectilinear XYZ-c.gt.s. coordinate system. That the most economical time distances between the two parallel planes and two parallel lines are coincident with perpendiculars to those parallel planes and lines does not impose any rectilinear profiling or structuring of the tetrahedron, which is a unique, four- planes-of-symmetry, self-structuring system, as the three-plane-defined cube of basic reference is not.
961.40 Granted: A Model for Six Degrees of Freedom: Granted the area of a triangle is base times one-half the altitude, with one given length of line AB marked on a flat plane and another infinitely extensible line number two lying in the same plane as short line AB, with line two parallel to AB; then connecting any point C on line two with both A and B will produce a constant-area triangle ABC. Holding AB fixed and moving only C in any direction on line two, the shape of triangle ABC will change, but its area will be constant. If we move C along line two in one direction the three edges will approach congruence with one another, appearing only as a line but being, in fact, a constant-area triangle.
961.41 Granted the volume of a tetrahedron is its base area times one-third of its altitude, we can now take the permitted, special condition discussed in Sec. 961.40 whereby C on line two is equidistant from both of line one's terminal-defining points A and B. We may next take a fourth point D, Lying in an infinitely extensible second plane which is parallel to the first infinitely extensible plane defined by points ABC. With D equidistant from A, B, and C, the volume of the regular tetrahedron ABCD will not be altered by letting D travel to any point in plane two while point C travels to any point on line two. Thus we learn that constant-volume tetrahedron ABCD might become so distended as to appear to be a line of no volume. Since there could be no volumeless line produced operationally, we may assume that all visible lines must be at minimum extended tetrahedra.
961.42 These variabilities of the constant-volume tetrahedron and its constant-area faces will permit congruence of the four vertexes of the tetrahedron with any four points of Universe by simply taking the initial distance AB to suit the task. This unit linear adjustment is a familiar wavelength tuning function. Here we have the six cosmic degrees of freedom (see Sec. 537.10); whereby we are free to choose the length of only one line to be held constant, while allowing the other five edge-lines of the tetrahedron to take any size. We can connect any four points in Universe and produce a tetrahedron that is matchable with whole, unit, rational-number, volume increments of the A and B Quanta Modules.
961.43 With large, clear plexiglass Models of the A and B Quanta Modules, we can easily see their clearly defined centers of volume. The centers of area of the triangular faces are arrived at by bisecting the edges and connecting the opposite angle. The center of volume of the tetrahedron is arrived at by interconnecting the four centers of triangular area with their opposite vertexes. These four lines constructed with fine, taut wires will converge to tangency at__and then diverge away from__the tetrahedron's center of volume.
961.44 The lines defining the center of four triangles and the center of volume inherently divide the modules into 24 equal parts. The same progressive subdivisions of the last 24 can be continued indefinitely, but each time we do so the rational bits become more and more asymmetrical. They get thinner and thinner and become more and more like glass splinters. By varying the frequency we can make any shape tetrahedron from the regular to the most asymmetric.
961.45 The modules make all the geometries__all the crystallography. Any probabilities can be dealt with. With the two of Euler: and Gibbs__the Me-and-Other- Awareness-the beginning of time, if there is time.... It starts testing the special cases that have time. They are absolutely quantized. The As are blue and the Bs are red. The blues and reds intertransform. Every sphere becomes a space, and every space becomes a sphere, palpitating in the wire model of electromagnetic wave action.
961.46 The A and B Quanta Modules become linear, as did the progression of concentric, common-base, uniform, linear, frequencied, electric-impulse conductors (see Sec. 923.21); and as also did the concentric, annually-frequencied, common-base-into- cone-rotated tetrahedra (see Sec. 541.30); the free energy put in at the base electronically, when you close the circuit at the beginning of the wire__you get the same package out at the other end, the same quanta. The longer the wire gets__or the tree grows__as it approaches parallelism, the more the energy packages begin to precess and to branch out at right angles.
961.47 Fluorescing occurs until all the juice is finally dissipated off the wire__or until all of this year's additional frequency's growth is realized in new branches, twigs, leaves and tetrahedrally-precessed buds. Birth: buds: A and B Modules; three-, four-, five-, and six-petallings: tetra, octa, icosa, rhombic-dodeca bud petals. The original input__the six A Quanta Modules of the original base tetrahedron__becomes distributive at 90 degrees. Coaxial cables tend to divert the precessional distributives inwardly to reduce the loss.
961.48 When great electrostatic charges built into clouds become dischargingly grounded (to Earth) by the excellently-conducting water of rain, and lightning occurs; we see the Earthward, precessionally-branching lightning. In grounding with Earth, lightning often closes its circuit through the tree's branches, whose liquid, water-filled, cell fibers are the most efficient conductors available in conducting the great electric charges inward to Earth through the trunk and the precessionally-distributive roots' branchings. Lines are tetrahedra. Lines can wave-bounce in ribbons and beams: tetra, octa, and icosa energy lock-up systems. E = Mc2. All tetra and only tetra are volumetric, i.e., quanta-immune to any and all transformation.
962.00 Powering in the Synergetics Coordinate System
962.01 In the operational conventions of the XYZ-c.gt.s. coordinate system of mathematics, physics, and chemistry, exponential powering meant the development of dimensions that require the introduction of successively new perpendiculars to planes not yet acquired by the system.
962.02 In synergetics, powering means only the frequency modulation of the system; i.e., subdivision of the system. In synergetics, we have only two directions: radial and circumferential.
962.03 In the XYZ system, three planes interact at 90 degrees (three dimensions). In synergetics, four planes interact at 60 degrees (four dimensions).
962.04 In synergetics there are four axial systems: ABCD. There is a maximum set of four planes nonparallel to one another but omnisymmetrically mutually intercepting. These are the four sets of the unique planes always comprising the isotropic vector matrix. The four planes of the tetrahedron can never be parallel to one another. The synergetics ABCD-four-dimensional and the conventional XYZ-three-dimensional systems are symmetrically intercoordinate. XYZ coordinate systems cannot rationally accommodate and directly articulate angular acceleration; and they can only awkwardly, rectilinearly articulate linear acceleration events.
962.05 Synergetic geometry discloses the rational fourth- and fifth-powering modelability of nature's coordinate transformings as referenced to the 60-degree equiangular isotropic-vector equilibrium.
962.06 XYZ volumetric coordination requires three times more volume to accommodate its dimensional results than does the 60-degree coordination calculating; therefore, XYZ 90-degree coordination cannot accommodate the fourth and fifth powers in its experimental demonstrability, i.e., modelability.
962.07 In the coordinate vectorial topology of synergetics, exponential powers and physical model dimensioning are identified with the number of vectors that may intercept the system at a constant angle, while avoiding parallelism or congruence with any other of the uniquely convergent vectors of the system.
962.10 Angular and Linear Accelerations: Synergetics accommodates the direct expression of both angular and linear accelerations of physical Universe. The frequency of the synergetics coordinate system, synchrosystem, simultaneously and directly expresses both the angular and linear accelerations of nature.
962.11 The Mass is the consequence of the angular accelerations. c2 or G2 of linear acceleration of the same unit inventory of forever regeneratively finite physical Universe, ever intertransforming and transacting in association (angular) or disassociation (linear) interaccelerations.
962.12 The "three-dimensional" XYZ-c.gt.s. system of coordination presently employed by world-around science can only express directly the linear accelerations and evolve therefrom its angular accelerations in awkward mathematics involving irrational, non-exactly-resolvable constants. c.gt.s. per second, M × F2 is cubistically awkwardized into calculatively tattering irrationality.
962.20 Convergence: In the topology of synergetics, powering is identifiable only with the uniangular vectorial convergences. The number of superficial, radiantly regenerated, vertex convergences of the system are identified with second powering, and not with anything we call "areas," that is, not with surfaces or with any experimentally demonstrable continuums.
962.30 Calculation of Local Events: All local events of Universe may be calculatively anticipated in synergetics by inaugurating calculation with a local vector- equilibrium frame and identifying the disturbance initiating point, direction, and energy of relative asymmetric pulsing of the introduced resonance and intertransformative event. (Synergetics Corollary, see Sec. 240.39.)
962.40 Time and Dimension: Synergetic geometry embraces all the qualities of experience, all aspects of being. Measurements of width, breadth, and height are awkward, inadequate descriptions that are only parts of the picture. Without weight, you do not exist physically; nor do you exist without a specific temperature. You can convert the velocity- times-mass into heat. Vectors are not abstractions, they are resolutions. Time and heat and length and weight are inherent in every dimension. Ergo, time is no more the fourth dimension than it is the first, second, or third dimension.
962.41 No time: No dimension. Time is dimension.
962.42 Time is in synergetic dimensioning because our geometry is vectorial. Every vector = mass × velocity, and time is a function of velocity. The velocity can be inward, outward, or around, and the arounding will always be chordal and exactly equated with the inwardness and outwardness time expendabilities. The Euclidian-derived XYZ coordinate geometry cannot express time equi-economically around, but only time in and time out. Synergetics inherently has time equanimity: it deals with anything that exists always in 1 × 1 time coordination.
962.50 Omnidirectional Regeneration: The coordinate systems of synergetics are omnidirectionally regenerative by both lines and planes parallel to the original converging set. The omnidirectional regeneration of synergetic coordination may always be expressed in always balanced equivalence terms either of radial or circumferential frequency increments.
Next Section: 963.00
Copyright © 1997 Estate of R. Buckminster Fuller