 Compound Curvature: Chords and Arcs
Compound Curvature: Chords and Arcs
1020.00  Compound Curvature: Chords and Arcs
Compound Curvature: Chords and Arcs

|
1021.10
 Convexity and Concavity of Tetrahedron
Convexity and Concavity of Tetrahedron
|

|
1021.11
 The outsides of systems are convex, and their insides
are concave. While
convexity diffuses radiation impinging upon it, concavity
concentrates radiation impinging
upon it; ergo, convexity and concavity are not the same.
The outsides of systems are convex, and their insides
are concave. While
convexity diffuses radiation impinging upon it, concavity
concentrates radiation impinging
upon it; ergo, convexity and concavity are not the same.
|

|
1021.12
 For every tetrahedron, there is one convex and one
concave. Because the
tetrahedron is inherently the minimum structural system
of Universe, it provides the
minimum omnicoexisting convexity and concavity condition
in Universe.
For every tetrahedron, there is one convex and one
concave. Because the
tetrahedron is inherently the minimum structural system
of Universe, it provides the
minimum omnicoexisting convexity and concavity condition
in Universe.
|

|
1021.13
 For every tetrahedron, there is an inside tetrahedron
and an outside
tetrahedron. For every convex spherical polyhedral geodesic
system, there is a concave
spherical polyhedral geodesic system. One cannot exist
without the other either in special
case or in sizeless eternal generalization. Spherical
arrays and compound curvature begin
with the tetrahedron.
For every tetrahedron, there is an inside tetrahedron
and an outside
tetrahedron. For every convex spherical polyhedral geodesic
system, there is a concave
spherical polyhedral geodesic system. One cannot exist
without the other either in special
case or in sizeless eternal generalization. Spherical
arrays and compound curvature begin
with the tetrahedron.
|

|
1022.10
 Minimum Sphere
Minimum Sphere
|

|
1022.11
 The transcendentally irrational constant pi (
The transcendentally irrational constant pi (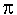 ) is
irrelevant to spherical
geodesic polyhedral array calculations because the minimum
sphere is a tetrahedron. We
have learned that a sphere as defined by the Greeks
is not experimentally demonstrable
because it would divide all Universe into outside and
inside and have no traffic between
the two. The Greek sphere as defined by them constituted
the first and nondemonstrable
perpetual-motion machine. Because there could be no
holes in it, the Greek sphere would
defy entropy. A sphere with no holes would be a continuum
or a solid, which are physical
conditions science has not found. We could dispense
with all Universe outside the Greek
sphere because Universe inside would be utterly conserved
and eternally adequate to itself,
independent of the rest of Universe outside. ) is
irrelevant to spherical
geodesic polyhedral array calculations because the minimum
sphere is a tetrahedron. We
have learned that a sphere as defined by the Greeks
is not experimentally demonstrable
because it would divide all Universe into outside and
inside and have no traffic between
the two. The Greek sphere as defined by them constituted
the first and nondemonstrable
perpetual-motion machine. Because there could be no
holes in it, the Greek sphere would
defy entropy. A sphere with no holes would be a continuum
or a solid, which are physical
conditions science has not found. We could dispense
with all Universe outside the Greek
sphere because Universe inside would be utterly conserved
and eternally adequate to itself,
independent of the rest of Universe outside.
|

|
1022.12
 What we do have experimentally as a sphere is an aggregate
of energy-event
foci approximately equidistant in approximately all
directions from one approximate
energy-event focus. This is a system in which the most
economical relationships between
embracingly adjacent foci are the greatcircle chords,
and not the arcs. This is why pi (
What we do have experimentally as a sphere is an aggregate
of energy-event
foci approximately equidistant in approximately all
directions from one approximate
energy-event focus. This is a system in which the most
economical relationships between
embracingly adjacent foci are the greatcircle chords,
and not the arcs. This is why pi (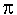 ) is
operationally irrelevant. Physics finds that nature
always employs the most economical
means. Being shorter, chordal distances are more economically
traversed than are
detouring arcs. All the chords between external points
of systems converge with one
another concavely and convexly, i.e., with the angles
around each external point always
adding to less than 360 degrees. They do not come together,
as do radii in a plane, with
360 degrees around each point. ) is
operationally irrelevant. Physics finds that nature
always employs the most economical
means. Being shorter, chordal distances are more economically
traversed than are
detouring arcs. All the chords between external points
of systems converge with one
another concavely and convexly, i.e., with the angles
around each external point always
adding to less than 360 degrees. They do not come together,
as do radii in a plane, with
360 degrees around each point.
|

|
1022.13
 The chords of an omnidirectional system always come
together with
concavity on one side and convexity on the other. The
angles never add up to 360
degrees, as do those formed on a plane by lines converging
radially upon a point. This is
why the long-held working assumption of mathematics__that
for an infinitesimal moment
a sphere is congruent with the plane to which it is
tangent__is invalid. Therefore, spherical
trigonometry, with its assumption of 360 degrees around
a point, is also invalid. Greek
spheres cannot be scientifically demonstrated. Almost-spherical
polyhedra are the nearest
approximation. It can only be treated with as polyhedral__as
an aggregate of points in
which the most economical relationships are chords;
ergo, geodesics .
The chords of an omnidirectional system always come
together with
concavity on one side and convexity on the other. The
angles never add up to 360
degrees, as do those formed on a plane by lines converging
radially upon a point. This is
why the long-held working assumption of mathematics__that
for an infinitesimal moment
a sphere is congruent with the plane to which it is
tangent__is invalid. Therefore, spherical
trigonometry, with its assumption of 360 degrees around
a point, is also invalid. Greek
spheres cannot be scientifically demonstrated. Almost-spherical
polyhedra are the nearest
approximation. It can only be treated with as polyhedral__as
an aggregate of points in
which the most economical relationships are chords;
ergo, geodesics .
|

|
1022.14
 If you find all the connections between all the points,
the system is
omnitriangulated. A spherical polyhedron is a high-frequency
geodesic polyhedron. Its
symmetric base may be tetrahedral, octahedral, or icosahedral;
but it may not be
hexagonal, i.e., with angles adding to 360 degrees around
each external point of the
system. The sum of all the angles around all the external
points of the superficially seeming
spherical systems will always add up to 720 degrees
less than the number of external
vertexes when each is multiplied by 360 degrees.
If you find all the connections between all the points,
the system is
omnitriangulated. A spherical polyhedron is a high-frequency
geodesic polyhedron. Its
symmetric base may be tetrahedral, octahedral, or icosahedral;
but it may not be
hexagonal, i.e., with angles adding to 360 degrees around
each external point of the
system. The sum of all the angles around all the external
points of the superficially seeming
spherical systems will always add up to 720 degrees
less than the number of external
vertexes when each is multiplied by 360 degrees.
|

|
1022.15
 In every geodesic sphere, you can always take out 12
pentagons. These 12
pentagons each drop out one triangle from the hexagonal
clusters around all other points.
Assuming the dropped-out triangles to be equiangular,
i.e., with 60-degree corners, this
means that 60 × 12 = 720°, which has been eliminated
from the total inventory of surface
angles. You can always find 12 pentagons on spherically
conformed systems such as
oranges, which are icosahedrally based; or four triangles
with 120-degree corners if the
system is tetrahedrally based; or six squares where
the system is octahedrally based.
In every geodesic sphere, you can always take out 12
pentagons. These 12
pentagons each drop out one triangle from the hexagonal
clusters around all other points.
Assuming the dropped-out triangles to be equiangular,
i.e., with 60-degree corners, this
means that 60 × 12 = 720°, which has been eliminated
from the total inventory of surface
angles. You can always find 12 pentagons on spherically
conformed systems such as
oranges, which are icosahedrally based; or four triangles
with 120-degree corners if the
system is tetrahedrally based; or six squares where
the system is octahedrally based.
|

|
1023.10
 Systematic Enclosure
Systematic Enclosure
|

|
1023.11
 If we get too semantically incisive, the reader may
lose all connection with
anything he has ever thought before. That might not
be a great loss. But we assume that
the reader can cope with his reflexes and make connections
between the old words and
new concepts with the new and more apt words. For example,
since physics has found no
continuums, we have had to clear up what we mean by
a sphere. It is not a surface; it is an
aggregate of events in close proximity. It isn't just
full of holes: it doesn't have any
continuum in which to have holes.
If we get too semantically incisive, the reader may
lose all connection with
anything he has ever thought before. That might not
be a great loss. But we assume that
the reader can cope with his reflexes and make connections
between the old words and
new concepts with the new and more apt words. For example,
since physics has found no
continuums, we have had to clear up what we mean by
a sphere. It is not a surface; it is an
aggregate of events in close proximity. It isn't just
full of holes: it doesn't have any
continuum in which to have holes.
|

|
1023.12
 The word polyhedron has to go because it says "many-sided,"
which implies
a continuum. We don't even have the faces. Faces become
spaces. They become intervals.
They become nothing. The Einsteinian finite Universe__an
aggregate nonsimultaneous
Universe__is predicated only on the absolute finiteness
of each local energy-event package
and the logic that an aggregate of finites is itself
finite.
The word polyhedron has to go because it says "many-sided,"
which implies
a continuum. We don't even have the faces. Faces become
spaces. They become intervals.
They become nothing. The Einsteinian finite Universe__an
aggregate nonsimultaneous
Universe__is predicated only on the absolute finiteness
of each local energy-event package
and the logic that an aggregate of finites is itself
finite.
|

|
1023.13
 The spheric experience is simply an ultrahigh frequency
of finite event
occurrences in respect to the magnitude of the tuning
perceptivity of the observer. (High
frequency to the human may be low frequency to the mosquito.)
The spheric experience is simply an ultrahigh frequency
of finite event
occurrences in respect to the magnitude of the tuning
perceptivity of the observer. (High
frequency to the human may be low frequency to the mosquito.)
|

|
1023.14
 If we get rid of the word polyhedra, then what word
do we have in its place?
A high-frequency, omnidirectional, spheric event system.
Polyhedra are finite system
enclosures. They are topologically describable, finite
system enclosures. They are Universe
dividers. They are not linear dividers, but omnidirectional
Universe dividers dividing
outside from inside, out from in. A mosquito has macro-micro
cosmos system perceptivity
at a different level from that of the whale's. Probably
each observer organism's stature
constitutes its spontaneous observational level of macro-micro
subdividing: bigger than
me; littler than me; within me; without me.
If we get rid of the word polyhedra, then what word
do we have in its place?
A high-frequency, omnidirectional, spheric event system.
Polyhedra are finite system
enclosures. They are topologically describable, finite
system enclosures. They are Universe
dividers. They are not linear dividers, but omnidirectional
Universe dividers dividing
outside from inside, out from in. A mosquito has macro-micro
cosmos system perceptivity
at a different level from that of the whale's. Probably
each observer organism's stature
constitutes its spontaneous observational level of macro-micro
subdividing: bigger than
me; littler than me; within me; without me.
|

|
1023.15
 We relinquish the word polyhedra to reemploy our new
term systematic
enclosure, which can be generalized to serve creatures
of any size__ i.e., a tetrahedron big
enough for a mosquito or big enough for a whale. Faces
are spaces, openings. The four
vertexes plus four faces plus six lines of the tetrahedron
must become four somethings
plus four nothings plus six relations. We add convergence
to something and divergence to
nothing__completely independent of size. Since there
are no "things," there is no
"something." We are talking of an event in pure principle.
We have events and no-events.
Events: novents: and relationships. Nature employs only
one or another of the most
equieconomical relationships. The most economical relationships
are geodesic, which
means most economical relationships. Ergo we have events
and novents: geodesics and
irrelevance. These are the epistemological stepping-stones.
We relinquish the word polyhedra to reemploy our new
term systematic
enclosure, which can be generalized to serve creatures
of any size__ i.e., a tetrahedron big
enough for a mosquito or big enough for a whale. Faces
are spaces, openings. The four
vertexes plus four faces plus six lines of the tetrahedron
must become four somethings
plus four nothings plus six relations. We add convergence
to something and divergence to
nothing__completely independent of size. Since there
are no "things," there is no
"something." We are talking of an event in pure principle.
We have events and no-events.
Events: novents: and relationships. Nature employs only
one or another of the most
equieconomical relationships. The most economical relationships
are geodesic, which
means most economical relationships. Ergo we have events
and novents: geodesics and
irrelevance. These are the epistemological stepping-stones.
|

|
1023.16
 The spheric experience is a high-frequency, omnidirectional
complex of
events and their relatedness. Since it is concerned
with the most economical relatedness,
we can also speak of it as a geodesic spherical experience.
This is where the importance of
chords comes in. A chord is abstract, yet tensive. A
chord has pull: we would probably not
think about the connections unless there was some pull
between them. The function of the
chords is to relate. The event is the vertex. The reaction
is the chord, the pulling away.
And the resultant is the inadvertent definition of the
nothingness of the areal and
volumetric spaces. The sequence is: Events; chords;
no-events. No-events = novents.
Areas do not create themselves; as with celestial constellations,
they are incidental to the
lines between the events. The faces are the bounding
of nothingness. Areas and volumes
are incidental resultants to finding the connections
between events of experience.
The spheric experience is a high-frequency, omnidirectional
complex of
events and their relatedness. Since it is concerned
with the most economical relatedness,
we can also speak of it as a geodesic spherical experience.
This is where the importance of
chords comes in. A chord is abstract, yet tensive. A
chord has pull: we would probably not
think about the connections unless there was some pull
between them. The function of the
chords is to relate. The event is the vertex. The reaction
is the chord, the pulling away.
And the resultant is the inadvertent definition of the
nothingness of the areal and
volumetric spaces. The sequence is: Events; chords;
no-events. No-events = novents.
Areas do not create themselves; as with celestial constellations,
they are incidental to the
lines between the events. The faces are the bounding
of nothingness. Areas and volumes
are incidental resultants to finding the connections
between events of experience.
|

|
1023.17
 Not only can there be no awareness until there is otherness
to be aware of,
but there can be no magnitude awareness with only one
otherness. You need two
otherness experiences with an interval between them
in order to have a sense of distance.
(Otherwise, you might just be looking at yourself in
a mirror.)
Not only can there be no awareness until there is otherness
to be aware of,
but there can be no magnitude awareness with only one
otherness. You need two
otherness experiences with an interval between them
in order to have a sense of distance.
(Otherwise, you might just be looking at yourself in
a mirror.)
|

|
1023.18
 You can have no sense awareness of shape with just
one otherness or two
othernesses. Shape awareness commences only with three
othernesses where the
relationship of three as a triangle has finite closure.
Shape is what you see areally, and until
there is closure, there is no area of otherness .
You can have no sense awareness of shape with just
one otherness or two
othernesses. Shape awareness commences only with three
othernesses where the
relationship of three as a triangle has finite closure.
Shape is what you see areally, and until
there is closure, there is no area of otherness .
|

|
1023.19
 Not until we have four othernesses do we have macrocosmic
volumetric
awareness. Four is required for substantive awareness.
Not until we have four othernesses do we have macrocosmic
volumetric
awareness. Four is required for substantive awareness.
|

|
1023.20
 System awareness begins when we find the otherness
surrounding us, when
we are omnidirectionally enclosed. The volume sense
is only from inside. From outside,
four points can look like one point or they can look
flat. Not until we turn a tetrahedron
inside out do we have microcosmic awareness. Not until
we swallow the otherness do we
have microcosmic volumetric awareness. We become the
outside. At first, we were just
the inside. In the womb. In the womb, we had tactile,
sensorial awareness of volumetric
surroundment by the otherness, but no visual, aural,
or olfactoral awareness of the
otherness surroundment. The child develops otherness
awareness only as outside
volumetric surroundment within which he finally discovers
me the observer, and me's
hand.
System awareness begins when we find the otherness
surrounding us, when
we are omnidirectionally enclosed. The volume sense
is only from inside. From outside,
four points can look like one point or they can look
flat. Not until we turn a tetrahedron
inside out do we have microcosmic awareness. Not until
we swallow the otherness do we
have microcosmic volumetric awareness. We become the
outside. At first, we were just
the inside. In the womb. In the womb, we had tactile,
sensorial awareness of volumetric
surroundment by the otherness, but no visual, aural,
or olfactoral awareness of the
otherness surroundment. The child develops otherness
awareness only as outside
volumetric surroundment within which he finally discovers
me the observer, and me's
hand.
|

|
1024.10
 What Is a Bubble?
What Is a Bubble?
|

|
1024.11
 What is a bubble? When oil is spilled on water__unfortunately,
an increasing
phenomenon__it spreads and spreads as a result of gravity
pulling and thinning it out. It
thins out because the molecules were piled on top of
one another. Gravity is pulling it into
single-molecule-thickness array. The individual molecules
are mass-interattracted, but the
attraction can be focused on the nearest molecules.
Molecules can therefore be tensed and
will yield in such a manner as to thin out their mass,
which can be stretched as a sheet or
stretched linearly__for each molecule holds on to only
those other molecules within
critical proximity.
What is a bubble? When oil is spilled on water__unfortunately,
an increasing
phenomenon__it spreads and spreads as a result of gravity
pulling and thinning it out. It
thins out because the molecules were piled on top of
one another. Gravity is pulling it into
single-molecule-thickness array. The individual molecules
are mass-interattracted, but the
attraction can be focused on the nearest molecules.
Molecules can therefore be tensed and
will yield in such a manner as to thin out their mass,
which can be stretched as a sheet or
stretched linearly__for each molecule holds on to only
those other molecules within
critical proximity.
|

|
1024.12
 As one floating molecule is surrounded by six other
floaters and the six are
surrounded by 12, or the next perimeter of 18, pulling
on one molecule distributes the pull
to six, and the six distribute the pull to 12, and the
12 distribute the pull to 18, and
therefore the original pull becomes proportionally reducible
and the relative distance
between the molecules varies from one surrounding hexagon
to the next. This relative
proximity brings about varying tension, which brings
about varying density. Varying
density, we learn in optics, brings about varying refraction
of light frequency, ergo, of light
as color, which accounts for the rainbow spectrum differentiating
witnessed as sunlight
strikes oil-covered waters. By passing light through
clear plexiglass structural models, the
structural strains as distributed throughout the plastic
mass are visually witnessable by the
red, orange, yellow, green, blue, violet rainbow spectrum.
As one floating molecule is surrounded by six other
floaters and the six are
surrounded by 12, or the next perimeter of 18, pulling
on one molecule distributes the pull
to six, and the six distribute the pull to 12, and the
12 distribute the pull to 18, and
therefore the original pull becomes proportionally reducible
and the relative distance
between the molecules varies from one surrounding hexagon
to the next. This relative
proximity brings about varying tension, which brings
about varying density. Varying
density, we learn in optics, brings about varying refraction
of light frequency, ergo, of light
as color, which accounts for the rainbow spectrum differentiating
witnessed as sunlight
strikes oil-covered waters. By passing light through
clear plexiglass structural models, the
structural strains as distributed throughout the plastic
mass are visually witnessable by the
red, orange, yellow, green, blue, violet rainbow spectrum.
|

|
1024.13
 Comprehending the mass-attracted, intertensed integrity
of molecules and
atoms, witness how the blacksmith can heat his metals
in the red-hot condition and
hammer the metal into varying shapes, all permitted
by the mass-interattraction of the
atoms themselves and their geometrical, methodical yielding
to rearrangement by forces
greater than their local surroundment interattractions.
The heating is done to accelerate
the atoms' electrons to decrease the relative-proximity
interattractiveness and
accommodate the geometrical rearranging of the atoms.
The cold metals, too, can be
hammered, but the energy-as-heat facilitates the rearranging.
When metals are reshaped,
they do so only as the absolute orderly intertransformative
geometry of closest packed
atoms permits.
Comprehending the mass-attracted, intertensed integrity
of molecules and
atoms, witness how the blacksmith can heat his metals
in the red-hot condition and
hammer the metal into varying shapes, all permitted
by the mass-interattraction of the
atoms themselves and their geometrical, methodical yielding
to rearrangement by forces
greater than their local surroundment interattractions.
The heating is done to accelerate
the atoms' electrons to decrease the relative-proximity
interattractiveness and
accommodate the geometrical rearranging of the atoms.
The cold metals, too, can be
hammered, but the energy-as-heat facilitates the rearranging.
When metals are reshaped,
they do so only as the absolute orderly intertransformative
geometry of closest packed
atoms permits.
|

|
1024.14
 Because the atoms and the molecules are subvisible
in magnitude to man, he
fails to detect the exquisite geometrical orderliness
with which they yield to rearrangement
while retaining the total interattractiveness occasioned
by their initial aggregation within
the critical limits of mass-attraction where the attractive
force overcomes the individual
orbiting integrity. The relative interattraction increases
as the second power of the rate at
which the interdistances diminish.
Because the atoms and the molecules are subvisible
in magnitude to man, he
fails to detect the exquisite geometrical orderliness
with which they yield to rearrangement
while retaining the total interattractiveness occasioned
by their initial aggregation within
the critical limits of mass-attraction where the attractive
force overcomes the individual
orbiting integrity. The relative interattraction increases
as the second power of the rate at
which the interdistances diminish.
|

|
1024.15
 The atomic proximity within the metals is of such a
high order as to give
high tensile strength, which is resistance to being
pulled or put asunder. Exquisite
magnitudes of interattractive proximities have nothing
to do with pressure. The
phenomenon is coherent density. Density is a pulling
together. (The error of reflexing is
here comparable to humans' misapprehending the wind's
"blowing" when we know that it
cannot blow; it can only be sucked.) Man is always thinking
he can push things when they
can only be pulled. Men are pushers. Women are attracters.
The atomic proximity within the metals is of such a
high order as to give
high tensile strength, which is resistance to being
pulled or put asunder. Exquisite
magnitudes of interattractive proximities have nothing
to do with pressure. The
phenomenon is coherent density. Density is a pulling
together. (The error of reflexing is
here comparable to humans' misapprehending the wind's
"blowing" when we know that it
cannot blow; it can only be sucked.) Man is always thinking
he can push things when they
can only be pulled. Men are pushers. Women are attracters.
|

|
1024.16
 These principles of interattractive strengths and orderly
geometrical yielding
to stresses are employed to a high degree in the manufacturing
of thin transparent plastic
sheets, such as all society is becoming familiar with
as a use product.
These principles of interattractive strengths and orderly
geometrical yielding
to stresses are employed to a high degree in the manufacturing
of thin transparent plastic
sheets, such as all society is becoming familiar with
as a use product.
|

|
1024.17
 Children are familiar with bubble gum. They are accustomed
to seeing the
bubble blown until suddenly it becomes transparent.
The membrane is yielding
circumferentially and tensilely to the pressure differential
between the outside atmosphere
and the multiplying molecules of gas inside literally
hitting the skin, trying to escape. When
the molecules of the bubble gum have rearranged themselves
in a geometrically orderly
manner so as to get the isotropic-vector matrix trussing
thinned down finally to a single
layer, then it has become transparent. Between the finite
Milky Way array, the atoms are
in sufficient proximity to hold their single-layer triangulation
array of hexagons within
hexagons. In this condition, bubbles show the same color
differentiation that reflects the
tensile variations: what humans have learned to call
surface-tension integrity.
Children are familiar with bubble gum. They are accustomed
to seeing the
bubble blown until suddenly it becomes transparent.
The membrane is yielding
circumferentially and tensilely to the pressure differential
between the outside atmosphere
and the multiplying molecules of gas inside literally
hitting the skin, trying to escape. When
the molecules of the bubble gum have rearranged themselves
in a geometrically orderly
manner so as to get the isotropic-vector matrix trussing
thinned down finally to a single
layer, then it has become transparent. Between the finite
Milky Way array, the atoms are
in sufficient proximity to hold their single-layer triangulation
array of hexagons within
hexagons. In this condition, bubbles show the same color
differentiation that reflects the
tensile variations: what humans have learned to call
surface-tension integrity.
|

|
1024.18
 In the way children blow up small rubber balloons,
you can almost see the
layers of molecules yielding as if unfolding like an
accordion, opening up angle after angle
as the balloon yields to stretch. The child witnesses
nature yielding to his own internal
pressures as nature thins out the atomic and molecular
arrangement with the most
exquisite delicacy of uniform thickness throughout the
stretching. The atoms and
molecules distribute the load superbly and open up the
many layers to one single layer
with a dimensional accuracy inherent in the unique prime
geometrical magnitudes of the
nucleus-electron orbit frequencies differentiating one
chemical element from the other in
absolute spectroscopic detectability throughout the
so-far-observed Universe. The
dimensional integrities are topological and vectorial
relative to all the characteristics with
which synergetics is concerned.
In the way children blow up small rubber balloons,
you can almost see the
layers of molecules yielding as if unfolding like an
accordion, opening up angle after angle
as the balloon yields to stretch. The child witnesses
nature yielding to his own internal
pressures as nature thins out the atomic and molecular
arrangement with the most
exquisite delicacy of uniform thickness throughout the
stretching. The atoms and
molecules distribute the load superbly and open up the
many layers to one single layer
with a dimensional accuracy inherent in the unique prime
geometrical magnitudes of the
nucleus-electron orbit frequencies differentiating one
chemical element from the other in
absolute spectroscopic detectability throughout the
so-far-observed Universe. The
dimensional integrities are topological and vectorial
relative to all the characteristics with
which synergetics is concerned.
|

|
1024.19
 Even as a child blows his bubble gum, the manufacturer
of plastic film first
extrudes plastic wire; in its most plastic state, its
end is conically pierced centrally while a
machine blows air into the pierced core (cone) of the
wire, which then yields in its
absolute geometrical orderliness of intermolecular and
interatomic integrities so that the
intruded gas stretches the progressively pulled-around
and conically intruded wire into a
thin, monometrically single-molecule thickness__or a
plurality of molecular thicknesses
directly and geometrically proportional to the pressure.
As the gas is introduced through
the apex of the piercer of the wire (like a micro-cratered
cone with a compressed air
"volcano" erupting from within it), it stretches the
wire into a bubble expanding at 180
degrees from the gas-introducing point; the now transparently
thin-skinned bubble is led
into and flatteningly gathered between metal rolls,
which progressively close to flatten the
bubble into a cylinder form until the whole cylinder
of thin film is cut, split, and finally
opened up to a single film: the evenness of the bubble
stretching has turned the skin of the
cylinder into a single sheet. The consistency of the
chemical aggregates that nature allows
chemists to produce in various chemical situations provides
varieties of thicknesses. Mylar
polyester, for instance, is inelastic and permits no
further yielding; it is not subject to
secondary deformation __stretching__such as occurs with
rubber. There eventually comes
a limit of the orderly rearrangeability of the atomic
and molecular structuring beyond
which it will no longer flex and at which point it breaks,
i.e., disconnects because
exceeding its critical-proximity interattraction limits.
The relative proximity of the atoms is
far more exquisite than that of molecules.
Even as a child blows his bubble gum, the manufacturer
of plastic film first
extrudes plastic wire; in its most plastic state, its
end is conically pierced centrally while a
machine blows air into the pierced core (cone) of the
wire, which then yields in its
absolute geometrical orderliness of intermolecular and
interatomic integrities so that the
intruded gas stretches the progressively pulled-around
and conically intruded wire into a
thin, monometrically single-molecule thickness__or a
plurality of molecular thicknesses
directly and geometrically proportional to the pressure.
As the gas is introduced through
the apex of the piercer of the wire (like a micro-cratered
cone with a compressed air
"volcano" erupting from within it), it stretches the
wire into a bubble expanding at 180
degrees from the gas-introducing point; the now transparently
thin-skinned bubble is led
into and flatteningly gathered between metal rolls,
which progressively close to flatten the
bubble into a cylinder form until the whole cylinder
of thin film is cut, split, and finally
opened up to a single film: the evenness of the bubble
stretching has turned the skin of the
cylinder into a single sheet. The consistency of the
chemical aggregates that nature allows
chemists to produce in various chemical situations provides
varieties of thicknesses. Mylar
polyester, for instance, is inelastic and permits no
further yielding; it is not subject to
secondary deformation __stretching__such as occurs with
rubber. There eventually comes
a limit of the orderly rearrangeability of the atomic
and molecular structuring beyond
which it will no longer flex and at which point it breaks,
i.e., disconnects because
exceeding its critical-proximity interattraction limits.
The relative proximity of the atoms is
far more exquisite than that of molecules.
|

|
1024.20
 Children experience magnets geometrically as metal
blocks with thickness,
length, and breadth. The magnet blocks can hold together
end to end, side to side, or even
point to point. You can stand them on their sides as
relatively structurally stable, like face-
bonding. But they regain flexibility when edge-bonded,
or even more so when point-
bonded.
Children experience magnets geometrically as metal
blocks with thickness,
length, and breadth. The magnet blocks can hold together
end to end, side to side, or even
point to point. You can stand them on their sides as
relatively structurally stable, like face-
bonding. But they regain flexibility when edge-bonded,
or even more so when point-
bonded.
|

|
1024.21
 The bubble gum, the wire film, or the balloon all display
invisible pneumatics
evenly distributing the tensive energy loads to produce
films of uniform thickness. No man
could hammer or roll a substance into such exquisite
dimensional stability. The popular
image has the blacksmith working his will on the semimolten
metal, but it is not so. The
great armorers and swordmakers found just the opposite;
they discovered the way in
which nature permits the metals to yield and still retain
their integrity. Humans cannot see
the rearrangements of mountain-reflecting lake waters
in atomical and molecular
"Between-the-Halves" marching maneuvers to halve at
the state of ice; this was arrived at,
however, in ever-orderly intertransforming, geometrical
integrity, invisible-to-humans
magnitude of perception and analysis.
The bubble gum, the wire film, or the balloon all display
invisible pneumatics
evenly distributing the tensive energy loads to produce
films of uniform thickness. No man
could hammer or roll a substance into such exquisite
dimensional stability. The popular
image has the blacksmith working his will on the semimolten
metal, but it is not so. The
great armorers and swordmakers found just the opposite;
they discovered the way in
which nature permits the metals to yield and still retain
their integrity. Humans cannot see
the rearrangements of mountain-reflecting lake waters
in atomical and molecular
"Between-the-Halves" marching maneuvers to halve at
the state of ice; this was arrived at,
however, in ever-orderly intertransforming, geometrical
integrity, invisible-to-humans
magnitude of perception and analysis.
|

|
1024.22
 Man talks carelessly and ignorantly of such words as
chaos ... turbulence ... turmoil ... and (the popular, modern) pollution
... where nothing but absolute order is
subvisibly maintained by nature and her transformation
arrangements unfamiliar to man.
Universe does not have any pollution. All the chemistries
of Universe are always essential
to the integrity of eternal intertransformation and
eternal self-regeneration.
Man talks carelessly and ignorantly of such words as
chaos ... turbulence ... turmoil ... and (the popular, modern) pollution
... where nothing but absolute order is
subvisibly maintained by nature and her transformation
arrangements unfamiliar to man.
Universe does not have any pollution. All the chemistries
of Universe are always essential
to the integrity of eternal intertransformation and
eternal self-regeneration.Physicists invent nothing. Chemists invent nothing. ... They find out what nature does from time to time and learn something of what her laws of rearrangement may be, and fortunate humans employ those rules to cooperate consciously with nature's evolution. |

|
1024.23
 All humans, endowed at birth with a billion capabilities
beyond the
knowledge of the parents, evolve in ways that are an
utter mystery to them. The exquisite,
myriadly endowed child employs that mysterious endowment
and intuitionally apprehends
itself as inventor of ways of using the orderly laws
of Universe to produce tools,
substances, and service integrities, to communicate
and allow humans to participate in
Universe's ever-transforming evolutionary events in
an as yet preposterously meager
degree, which has given rise to a nature-permitted variety
of little humans on tiny planet
Earth each becoming Mr. Big, with a suddenly mistaken
sense of power over
environmental transformations__participation in which
permitted him to feel himself as a
manager of inventories of logistical multiplicity which,
at the most ignorant level,
manifests itself as politically assured mandates and
political-world gambling = gamboling =
ideological warfare = national sovereignties = morally
rationalizing public = body politic =
individual nations as United Nations.
All humans, endowed at birth with a billion capabilities
beyond the
knowledge of the parents, evolve in ways that are an
utter mystery to them. The exquisite,
myriadly endowed child employs that mysterious endowment
and intuitionally apprehends
itself as inventor of ways of using the orderly laws
of Universe to produce tools,
substances, and service integrities, to communicate
and allow humans to participate in
Universe's ever-transforming evolutionary events in
an as yet preposterously meager
degree, which has given rise to a nature-permitted variety
of little humans on tiny planet
Earth each becoming Mr. Big, with a suddenly mistaken
sense of power over
environmental transformations__participation in which
permitted him to feel himself as a
manager of inventories of logistical multiplicity which,
at the most ignorant level,
manifests itself as politically assured mandates and
political-world gambling = gamboling =
ideological warfare = national sovereignties = morally
rationalizing public = body politic =
individual nations as United Nations.
|

|
1024.24
 Stress-producing metaphysical gas stretches and strains
nature to yield into
social-evolution conformations such as the gas-filled
plastic tube of Universe. There is an
a priori universal law in the controlled complexity
that tolerates man's pressurized
nonsense, as nature permits each day's seemingly new
Universe of semifamiliarities,
semiwonders, and semimystery, what humans might think
of as history unfolding on this
little planet. There is the Game of Cosmic History,
in which Universe goes on
approximately unaware of human nonsense while accommodating
its omnilocal game-
playing. Flies have their game. Mosquitoes have their
game. Microbes have their game.
Lion cubs have their game. Whatever games they may be
playing, positive or negative,
realistic or make-believe, all the games are fail-safe,
alternate circuits, omniconsequential
to eternally regenerative Universe integrity. It's all
permitted. It all belongs.
Stress-producing metaphysical gas stretches and strains
nature to yield into
social-evolution conformations such as the gas-filled
plastic tube of Universe. There is an
a priori universal law in the controlled complexity
that tolerates man's pressurized
nonsense, as nature permits each day's seemingly new
Universe of semifamiliarities,
semiwonders, and semimystery, what humans might think
of as history unfolding on this
little planet. There is the Game of Cosmic History,
in which Universe goes on
approximately unaware of human nonsense while accommodating
its omnilocal game-
playing. Flies have their game. Mosquitoes have their
game. Microbes have their game.
Lion cubs have their game. Whatever games they may be
playing, positive or negative,
realistic or make-believe, all the games are fail-safe,
alternate circuits, omniconsequential
to eternally regenerative Universe integrity. It's all
permitted. It all belongs.
|

|
1024.25
 Only humans play "Deceive yourself and you can fool
the world"; or "I
know what it's all about"; or "Life is just chemistry";
and "We humans invented and are
running the world." Dogs play "Fetch it" to please their
masters, not to deceive
themselves. The most affectionate of dogs do not play
"Burial of our dead"__"Chemistry
is for real." Only humans play the game of game of masks
and monuments. Fictional
history. Historical architecture. Crabs walk sideways;
but only human society keeps its
eyes on the past as it backs into its future. Madison
Avenue aesthetics and ethics. Comic
strips and cartoons ... truth emergent, laughing at
self-deception ... momentary, fleeting
glimpses of the glory, inadvertently revealed through
faithful accuracy of observation__
lucid conceptioning__spoken of as the music of the stars,
inadequate to the mystery of
integrity ...
Only humans play "Deceive yourself and you can fool
the world"; or "I
know what it's all about"; or "Life is just chemistry";
and "We humans invented and are
running the world." Dogs play "Fetch it" to please their
masters, not to deceive
themselves. The most affectionate of dogs do not play
"Burial of our dead"__"Chemistry
is for real." Only humans play the game of game of masks
and monuments. Fictional
history. Historical architecture. Crabs walk sideways;
but only human society keeps its
eyes on the past as it backs into its future. Madison
Avenue aesthetics and ethics. Comic
strips and cartoons ... truth emergent, laughing at
self-deception ... momentary, fleeting
glimpses of the glory, inadvertently revealed through
faithful accuracy of observation__
lucid conceptioning__spoken of as the music of the stars,
inadequate to the mystery of
integrity ...
 All the poetry,. All the poetry,.
 all the chemistry, all the chemistry,
 all the stars, all the stars,
... are permitted transformations of all the eternal integrity.  All the constants, All the constants,
 gravitational constant, gravitational constant,
 radiational constant, radiational constant,
 Planck's constant, Planck's constant,
... above all, mathematics, geometry, physics, are only manifests of the eternal mysteries, love, harmonic integrity beyond further words.  The isotropic vector
matrix yields to palm trees and
jellyfish as a complex of
mathematical integrities. As one will always be to one
other. But no other: no one. Other
is four. No four__but whereas one has no relations; two
have only one interrelationship;
three have three interrelationships; but four have a
minimum of six relationships
synergetics. No insideness without four. Without four,
no womb: no birth: no life ... the
dawning awareness of the integrity of Universe. For
humanity the only permitted infallibly
predictable is the eternal cosmic integrity. The isotropic vector
matrix yields to palm trees and
jellyfish as a complex of
mathematical integrities. As one will always be to one
other. But no other: no one. Other
is four. No four__but whereas one has no relations; two
have only one interrelationship;
three have three interrelationships; but four have a
minimum of six relationships
synergetics. No insideness without four. Without four,
no womb: no birth: no life ... the
dawning awareness of the integrity of Universe. For
humanity the only permitted infallibly
predictable is the eternal cosmic integrity.
|

|
1025.10
 Closest Packing of Bubbles
Closest Packing of Bubbles
|

|
1025.11
 Isolated bubbles are systematic spheric enclosures.
Bubbles are convex and
spheric because spheres accommodate the most volume
with the least surface, and the
pressure differential between inside and outside atmosphere
makes them belly out. The
enclosing "surfaces" of bubbles are in fact critical-proximity
events that produce so-called
"surface tension," which is, more accurately, single-molecule-thickness,
omnitriangular,
mass-interattracted atoms surrounding a gas whose would-be
kinetically escaping
molecules are larger than the intervals between the
spherical membrane's atomic event
proximities.
Isolated bubbles are systematic spheric enclosures.
Bubbles are convex and
spheric because spheres accommodate the most volume
with the least surface, and the
pressure differential between inside and outside atmosphere
makes them belly out. The
enclosing "surfaces" of bubbles are in fact critical-proximity
events that produce so-called
"surface tension," which is, more accurately, single-molecule-thickness,
omnitriangular,
mass-interattracted atoms surrounding a gas whose would-be
kinetically escaping
molecules are larger than the intervals between the
spherical membrane's atomic event
proximities.
|

|
1025.12
 Bubbles aggregate in the manner of closest-packed uniradius
spheres but
behave differently as they aggregate. Only the outer
surfaces of the outermost bubbles in
the aggregate retain their convex surfaces. Within the
aggregate, all the bubbles' pressures
become approximately uniform; therefore, relieved of
the pneumatic pressure differential
between insideness and outsideness, they contract from
convex to approximately planar
membranes. Here, what would have been spaces between
the spheres become planar-
bound system enclosures (polyhedra), as do also the
corresponding concave octahedra and
vector equilibria of hard-shell uniradius spheres in
closest packing.
Bubbles aggregate in the manner of closest-packed uniradius
spheres but
behave differently as they aggregate. Only the outer
surfaces of the outermost bubbles in
the aggregate retain their convex surfaces. Within the
aggregate, all the bubbles' pressures
become approximately uniform; therefore, relieved of
the pneumatic pressure differential
between insideness and outsideness, they contract from
convex to approximately planar
membranes. Here, what would have been spaces between
the spheres become planar-
bound system enclosures (polyhedra), as do also the
corresponding concave octahedra and
vector equilibria of hard-shell uniradius spheres in
closest packing.
|

|
1025.13
 Because the bubbles are rarely of unit radius, the
closest-packed bubble
"polyhedra," corresponding to the closest-packed spheres,
disclose only multifrequency-
permitted varieties of tensional membrane interfaceting.
Yet the fundamental
interrelatedness of the seemingly disorderly subdividing
of bubble aggregates is elegantly
identified with the absolute order of the isotropic
vector matrix, in that all the internal
polyhedra manifest 14 facets each, though a variety
of polygonal shapes and sizes. This
ness is also manifest in the closest interpacking of
biological cells.
Because the bubbles are rarely of unit radius, the
closest-packed bubble
"polyhedra," corresponding to the closest-packed spheres,
disclose only multifrequency-
permitted varieties of tensional membrane interfaceting.
Yet the fundamental
interrelatedness of the seemingly disorderly subdividing
of bubble aggregates is elegantly
identified with the absolute order of the isotropic
vector matrix, in that all the internal
polyhedra manifest 14 facets each, though a variety
of polygonal shapes and sizes. This
ness is also manifest in the closest interpacking of
biological cells.
|

|
1025.14
 The 14 internal facets correspond exactly with the
vector equilibrium's 14
faces__eight triangular and six square__which 14-ness,
in turn, is directly identifiable with
the tetrahedron's sum total of topological aspects:
4 vertexes + 4 faces + 6 edges = 14; as
may be experimentally demonstrated with high-frequency
tetrahedra, each of whose four
vertexes may be truncated, providing four additional
triangular facets; and each of whose
six edges may be truncated (most crystals have truncated
edges), providing six additional
rectilinear facets whose terminal ends will now convert
the four previous triangular
truncated corners into four hexagons. With high-frequency
tetrahedra, each of the
truncations can be accommodated at different lengths.
The truncated tetrahedron's total of
facets consisting of eight hexagons and six rectangles
may be of a great variety of edge
lengths, which variety tends to mislead the observer
into thinking of the aggregate as being
disorderly.
The 14 internal facets correspond exactly with the
vector equilibrium's 14
faces__eight triangular and six square__which 14-ness,
in turn, is directly identifiable with
the tetrahedron's sum total of topological aspects:
4 vertexes + 4 faces + 6 edges = 14; as
may be experimentally demonstrated with high-frequency
tetrahedra, each of whose four
vertexes may be truncated, providing four additional
triangular facets; and each of whose
six edges may be truncated (most crystals have truncated
edges), providing six additional
rectilinear facets whose terminal ends will now convert
the four previous triangular
truncated corners into four hexagons. With high-frequency
tetrahedra, each of the
truncations can be accommodated at different lengths.
The truncated tetrahedron's total of
facets consisting of eight hexagons and six rectangles
may be of a great variety of edge
lengths, which variety tends to mislead the observer
into thinking of the aggregate as being
disorderly.
|
1030.00
 Omniequilibrium
Omniequilibrium

|
1030.10
 Omniequilibrium of Vector Equilibrium: I seek a word
to express most
succinctly the complexedly pulsative, inside-outing,
integrative-disintegrative,
countervailing behaviors of the vector equilibrium.
"Librium" represents the degrees of
freedom. Universe is omnilibrious because it accommodates
all the every-time-recurrent,
alternatively-optional degrees of equieconomical freedoms.
Omniequilibrious means all
the foregoing.
Omniequilibrium of Vector Equilibrium: I seek a word
to express most
succinctly the complexedly pulsative, inside-outing,
integrative-disintegrative,
countervailing behaviors of the vector equilibrium.
"Librium" represents the degrees of
freedom. Universe is omnilibrious because it accommodates
all the every-time-recurrent,
alternatively-optional degrees of equieconomical freedoms.
Omniequilibrious means all
the foregoing.
|

|
1030.11
 The sphere is a convex vector equilibrium, and the
spaces between closest-
packed uniradius spheres are the concave vector equilibria
or, in their contractive form,
the concave octahedra. In going contractively from vector
equilibrium to equi-vector-
edged tetrahedron (see Sec.
460), we go from a volumetric
20-ness to a volumetric
oneness, a twentyfold contraction. In the vector-equilibrium
jitterbug, the axis does not
rotate, but the equator does. On the other hand, if
you hold the equator and rotate the
axis, the system contracts. Twisting one end of the
axis to rotate it terminates the
jitterbug's 20-volume to 4-volume octahedral state contraction,
whereafter the contraction
momentum throws a torque in the system with a leverage
force of 20 to 1. It contracts
until it becomes a volume of one as a quadrivalent tetrahedron,
that is, with the four edges
of the tetrahedron congruent. Precessionally aided by
other galaxies' mass-attractive
tensional forces acting upon them to accelerate their
axial, twist-and-torque-imposed
contractions, this torque momentum may account for the
way stars contract into dwarfs
and pulsars, or for the way that galaxies pulsate or
contract into the incredibly vast and
dense, paradoxically named "black holes."
The sphere is a convex vector equilibrium, and the
spaces between closest-
packed uniradius spheres are the concave vector equilibria
or, in their contractive form,
the concave octahedra. In going contractively from vector
equilibrium to equi-vector-
edged tetrahedron (see Sec.
460), we go from a volumetric
20-ness to a volumetric
oneness, a twentyfold contraction. In the vector-equilibrium
jitterbug, the axis does not
rotate, but the equator does. On the other hand, if
you hold the equator and rotate the
axis, the system contracts. Twisting one end of the
axis to rotate it terminates the
jitterbug's 20-volume to 4-volume octahedral state contraction,
whereafter the contraction
momentum throws a torque in the system with a leverage
force of 20 to 1. It contracts
until it becomes a volume of one as a quadrivalent tetrahedron,
that is, with the four edges
of the tetrahedron congruent. Precessionally aided by
other galaxies' mass-attractive
tensional forces acting upon them to accelerate their
axial, twist-and-torque-imposed
contractions, this torque momentum may account for the
way stars contract into dwarfs
and pulsars, or for the way that galaxies pulsate or
contract into the incredibly vast and
dense, paradoxically named "black holes."
|

|
1030.20
 Gravitational Zone System: There is no pointal center
of gravity. There is
a gravitational-zone-system, a zone of concentration
with minimum-maximum zone
system limits. Vertex is in convergence, and face is
in divergence. Synergetics geometry
precession explains radial-circumferential accelerational
transformations.
Gravitational Zone System: There is no pointal center
of gravity. There is
a gravitational-zone-system, a zone of concentration
with minimum-maximum zone
system limits. Vertex is in convergence, and face is
in divergence. Synergetics geometry
precession explains radial-circumferential accelerational
transformations.
|

|
1031.10
 Dynamic Symmetry
Dynamic Symmetry
|

|
1031.11
 When we make the geodesic subdivisions of symmetrically
omnitriangulated
systems, the three corner angles increase to add up
to more than 180 degrees because they
are on a sphere. If we deproject them back to the icosahedron,
they become symmetrical
again, adding to exactly 180 degrees. They are asymmetrical
only because they are
projected out onto the sphere. We know that each corner
of a two-frequency spherical
icosahedron has an isosceles triangle with an equilateral
triangle in the center. In a four-
frequency spherical icosahedron there are also six scalenes:
three positive and three
negative sets of scalenes, so they balance each other.
That is, they are dynamically
symmetrical. By themselves, the scalenes are asymmetrical.
This is synergy. This is the
very essence of our Universe. Everything that you and
I can observe or sense is an
asymmetrical aspect of only sum-totally and nonunitarily-conceptual,
omnisymmetrical
Universe.
When we make the geodesic subdivisions of symmetrically
omnitriangulated
systems, the three corner angles increase to add up
to more than 180 degrees because they
are on a sphere. If we deproject them back to the icosahedron,
they become symmetrical
again, adding to exactly 180 degrees. They are asymmetrical
only because they are
projected out onto the sphere. We know that each corner
of a two-frequency spherical
icosahedron has an isosceles triangle with an equilateral
triangle in the center. In a four-
frequency spherical icosahedron there are also six scalenes:
three positive and three
negative sets of scalenes, so they balance each other.
That is, they are dynamically
symmetrical. By themselves, the scalenes are asymmetrical.
This is synergy. This is the
very essence of our Universe. Everything that you and
I can observe or sense is an
asymmetrical aspect of only sum-totally and nonunitarily-conceptual,
omnisymmetrical
Universe.
|

|
1031.12
 Geodesic sphere triangulation is the high-frequency
subdivision of the
surface of a sphere beyond the icosahedron. You cannot
have omnisymmetrical, equiangle
and equiedged, triangular, system subdivisioning in
greater degree than that of the
icosahedron's 20 similar triangles.
Geodesic sphere triangulation is the high-frequency
subdivision of the
surface of a sphere beyond the icosahedron. You cannot
have omnisymmetrical, equiangle
and equiedged, triangular, system subdivisioning in
greater degree than that of the
icosahedron's 20 similar triangles.
|

|
1031.13
 As we have learned, there are only three prime structural
systems of
Universe: tetrahedron, octahedron, and icosahedron.
When these are projected on to a
sphere, they produce the spherical tetrahedron, the
spherical octahedron, and the spherical
icosahedron, all of whose corner angles are much larger
than their chordal, flat-faceted,
polyhedral counterpart corners. In all cases, the corners
are isosceles triangles, and, in the
even frequencies, the central triangles are equilateral,
and are surrounded by further
symmetrically balanced sets of positive and negative
scalenes. The higher the frequency,
the more the scalenes. But since the positive and negative
scalenes always appear in equal
abundance, they always cancel one another out as dynamically
complementarily
equilateral. This is all due to the fact that they are
projections outwardly onto a sphere of
the original tetrahedron, octahedron, or icosahedron,
which as planar surfaces could be
subdivided into high-frequency triangles without losing
any of their fundamental similarity
and symmetry.
As we have learned, there are only three prime structural
systems of
Universe: tetrahedron, octahedron, and icosahedron.
When these are projected on to a
sphere, they produce the spherical tetrahedron, the
spherical octahedron, and the spherical
icosahedron, all of whose corner angles are much larger
than their chordal, flat-faceted,
polyhedral counterpart corners. In all cases, the corners
are isosceles triangles, and, in the
even frequencies, the central triangles are equilateral,
and are surrounded by further
symmetrically balanced sets of positive and negative
scalenes. The higher the frequency,
the more the scalenes. But since the positive and negative
scalenes always appear in equal
abundance, they always cancel one another out as dynamically
complementarily
equilateral. This is all due to the fact that they are
projections outwardly onto a sphere of
the original tetrahedron, octahedron, or icosahedron,
which as planar surfaces could be
subdivided into high-frequency triangles without losing
any of their fundamental similarity
and symmetry.
|

|
1031.14
 In other words, the planar symmetrical is projected
outwardly on the sphere.
The sphere is simply a palpitation of what was the symmetrical
vector equilibrium, an
oscillatory pulsation, inwardly and outwardly__an extension
onto an asymmetrical surface
of what is inherently symmetrical, with the symmetricals
going into higher frequency. (See
Illus.
1032.12,
1032.30, and
1032.31.)
In other words, the planar symmetrical is projected
outwardly on the sphere.
The sphere is simply a palpitation of what was the symmetrical
vector equilibrium, an
oscillatory pulsation, inwardly and outwardly__an extension
onto an asymmetrical surface
of what is inherently symmetrical, with the symmetricals
going into higher frequency. (See
Illus.
1032.12,
1032.30, and
1032.31.)
|

|
1031.15
 What we are talking about as apparent asymmetry is
typical of all life. Nature
refuses to stop at the vector-equilibrium phase and
always is caught in one of its
asymmetric aspects: the positive and negative, inward
and outward, or circumferentially
askew alterations.
What we are talking about as apparent asymmetry is
typical of all life. Nature
refuses to stop at the vector-equilibrium phase and
always is caught in one of its
asymmetric aspects: the positive and negative, inward
and outward, or circumferentially
askew alterations.
|

|
1031.16
 Asymmetry is a consequence of the phenomenon time and
time a
consequence of the phenomenon we call afterimage, or
"double-take," or reconsideration,
with inherent lags of recallability rates in respect
to various types of special-case
experiences. Infrequently used names take longer to
recall than do familiar actions. So the
very consequence of only "dawning" and evolving (never
instantaneous) awareness is to
impose the phenomenon time upon an otherwise timeless,
ergo eternal Universe.
Awareness itself is in all these asymmetries, and the
pulsations are all the consequences of
just thought itself: the ability of Universe to consider
itself, and to reconsider itself. (See
Sec.
529.09.)
Asymmetry is a consequence of the phenomenon time and
time a
consequence of the phenomenon we call afterimage, or
"double-take," or reconsideration,
with inherent lags of recallability rates in respect
to various types of special-case
experiences. Infrequently used names take longer to
recall than do familiar actions. So the
very consequence of only "dawning" and evolving (never
instantaneous) awareness is to
impose the phenomenon time upon an otherwise timeless,
ergo eternal Universe.
Awareness itself is in all these asymmetries, and the
pulsations are all the consequences of
just thought itself: the ability of Universe to consider
itself, and to reconsider itself. (See
Sec.
529.09.)
|

|
1032.00
 Convex and Concave Sphere-Packing Intertransformings
Convex and Concave Sphere-Packing Intertransformings
|

|
1032.10
 Convex and Concave Sphere-Packing Intertransformings
as the Energy
Patterning Between Spheres and Spaces of Omni-Closest-Packed
Spheres and Their
Isotropic-Vector-Matrix Field: When closest-packed uniradius
spheres are interspersed
with spaces, there are only two kinds of spaces interspersing
the closest-packed spheres:
the concave octahedron and the concave vector equilibrium.
The spheres themselves are
convex vector equilibria complementing the concave octahedra
and the concave vector
equilibria. (See Secs.
970.10
and
970.20.)
Convex and Concave Sphere-Packing Intertransformings
as the Energy
Patterning Between Spheres and Spaces of Omni-Closest-Packed
Spheres and Their
Isotropic-Vector-Matrix Field: When closest-packed uniradius
spheres are interspersed
with spaces, there are only two kinds of spaces interspersing
the closest-packed spheres:
the concave octahedron and the concave vector equilibrium.
The spheres themselves are
convex vector equilibria complementing the concave octahedra
and the concave vector
equilibria. (See Secs.
970.10
and
970.20.)
|

|
1032.11
 The spheres and spaces are rationally one-quantum-jump,
volumetrically
coordinate, as shown by the rhombic dodecahedron's sphere-and-space,
and share sixness
of volume in respect to the same nuclear sphere's own
exact fiveness of volume (see Secs.
985.07 and
985.08),
the morphological dissimilarity
of which render them one-quantumly
disequilibrious, i.e., asymmetrical phases of the vector
equilibrium's complex of both
alternate and coincident transformabilities. They are
involutionally-evolutionally, inward-
outward, twist-around, fold-up and unfold, multifrequencied
pulsations of the vector
equilibria. By virtue of these transformations and their
accommodating volumetric
involvement, the spheres and spaces are interchangeably
intertransformative. For instance,
each one can be either a convex or a concave asymmetry
of the vector equilibrium, as the
"jitterbug" has demonstrated (Sec.
460). The vector
equilibrium contracts from its
maximum isotropic-vector-matrix radius in order to become
a sphere. That is how it can
be accommodated within the total isotropic-vector-matrix
field of reference.
The spheres and spaces are rationally one-quantum-jump,
volumetrically
coordinate, as shown by the rhombic dodecahedron's sphere-and-space,
and share sixness
of volume in respect to the same nuclear sphere's own
exact fiveness of volume (see Secs.
985.07 and
985.08),
the morphological dissimilarity
of which render them one-quantumly
disequilibrious, i.e., asymmetrical phases of the vector
equilibrium's complex of both
alternate and coincident transformabilities. They are
involutionally-evolutionally, inward-
outward, twist-around, fold-up and unfold, multifrequencied
pulsations of the vector
equilibria. By virtue of these transformations and their
accommodating volumetric
involvement, the spheres and spaces are interchangeably
intertransformative. For instance,
each one can be either a convex or a concave asymmetry
of the vector equilibrium, as the
"jitterbug" has demonstrated (Sec.
460). The vector
equilibrium contracts from its
maximum isotropic-vector-matrix radius in order to become
a sphere. That is how it can
be accommodated within the total isotropic-vector-matrix
field of reference.
|
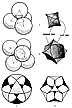 Fig. 1032.12 |
1032.12
 As the vector equilibrium's radii contract linearly,
in the exact manner of a
coil spring contracting, the 24 edges of one-half of
all the vector equilibria bend
outwardly, becoming arcs of spheres. At the same time,
the chords of the other half of all
the vector equilibria curve inwardly to produce either
concave-faced vector-equilibria
spaces between the spheres or to form concave octahedra
spaces between the spheres, as
in the isotropic-vector-matrix field model (see Illus.
1032.12). Both the spheric aspect of
the vector equilibrium and the "space" aspect are consequences
of the coil-spring-like
contraction and consequent chordal "outward" and "inward"
arcing complementation of
alternately, omnidirectionally adjacent vector equilibria
of the isotropic-vector-matrix
field.
As the vector equilibrium's radii contract linearly,
in the exact manner of a
coil spring contracting, the 24 edges of one-half of
all the vector equilibria bend
outwardly, becoming arcs of spheres. At the same time,
the chords of the other half of all
the vector equilibria curve inwardly to produce either
concave-faced vector-equilibria
spaces between the spheres or to form concave octahedra
spaces between the spheres, as
in the isotropic-vector-matrix field model (see Illus.
1032.12). Both the spheric aspect of
the vector equilibrium and the "space" aspect are consequences
of the coil-spring-like
contraction and consequent chordal "outward" and "inward"
arcing complementation of
alternately, omnidirectionally adjacent vector equilibria
of the isotropic-vector-matrix
field.
|

|
1032.13
 In a tetrahedron composed of four spheres, the central
void is an octahedron
with four concave spherical triangular faces and four
planar triangular faces with concave
edges. This can be described as a concave octahedron.
In an octahedron composed of six
closest-packed spheres, the central void is a vector
equilibrium with six concave spherical
square faces and eight triangular faces with concave
edges: a concave vector equilibrium.
The vector equilibrium, with edges arced to form a sphere,
may be considered as a convex
vector equilibrium. Illus.
1032.12D
shows the vector
equilibrium with arcs on the
triangular faces defined by spheres tangent at vertexes:
a concave vector equilibrium.
In a tetrahedron composed of four spheres, the central
void is an octahedron
with four concave spherical triangular faces and four
planar triangular faces with concave
edges. This can be described as a concave octahedron.
In an octahedron composed of six
closest-packed spheres, the central void is a vector
equilibrium with six concave spherical
square faces and eight triangular faces with concave
edges: a concave vector equilibrium.
The vector equilibrium, with edges arced to form a sphere,
may be considered as a convex
vector equilibrium. Illus.
1032.12D
shows the vector
equilibrium with arcs on the
triangular faces defined by spheres tangent at vertexes:
a concave vector equilibrium.
|

|
1032.20
 Energy Wave Propagation: The shift between spheres
and spaces is
accomplished precessionally. You introduce just one
energy action__push or pull__into
the field, and its inertia provides the reaction to
your push or pull; the resultant propagates
the everywhere locally sphere-to-space, space-to-sphere
omni-intertransformations whose
comprehensive synergetic effect in turn propagates an
omnidirectional wave. Dropping a
stone in the water discloses a planar pattern of precessional
wave regeneration. The local
unit-energy force articulates an omnidirectional, spherically
expanding, four-dimensional
counterpart of the planar water waves' circular expansion.
The successive waves' curves
are seen generating and regenerating and are neither
simultaneous nor instantaneous.
Energy Wave Propagation: The shift between spheres
and spaces is
accomplished precessionally. You introduce just one
energy action__push or pull__into
the field, and its inertia provides the reaction to
your push or pull; the resultant propagates
the everywhere locally sphere-to-space, space-to-sphere
omni-intertransformations whose
comprehensive synergetic effect in turn propagates an
omnidirectional wave. Dropping a
stone in the water discloses a planar pattern of precessional
wave regeneration. The local
unit-energy force articulates an omnidirectional, spherically
expanding, four-dimensional
counterpart of the planar water waves' circular expansion.
The successive waves' curves
are seen generating and regenerating and are neither
simultaneous nor instantaneous.
|

|
1032.21
 The only instantaneity is eternity. All temporal (temporary)
equilibrium life-
time-space phenomena are sequential, complementary,
and orderly disequilibrious
intertransformations of space-nothingness to time-somethingness,
and vice versa. Both
space realizations and time realizations are always
of orderly asymmetric degrees of
discrete magnitudes. The hexagon is an instantaneous,
eternal, simultaneous, planar
section of equilibrium, wherein all the chords are vectors
exactly equal to all the vector
radii: six explosively disintegrative, compressively
coiled, wavilinear vectors exactly and
finitely contained by six chordal, tensively-coil-extended,
wavilinear vectors of equal
magnitude.
The only instantaneity is eternity. All temporal (temporary)
equilibrium life-
time-space phenomena are sequential, complementary,
and orderly disequilibrious
intertransformations of space-nothingness to time-somethingness,
and vice versa. Both
space realizations and time realizations are always
of orderly asymmetric degrees of
discrete magnitudes. The hexagon is an instantaneous,
eternal, simultaneous, planar
section of equilibrium, wherein all the chords are vectors
exactly equal to all the vector
radii: six explosively disintegrative, compressively
coiled, wavilinear vectors exactly and
finitely contained by six chordal, tensively-coil-extended,
wavilinear vectors of equal
magnitude.
|

|
1032.22
 Physics thought it had found only two kinds of acceleration:
linear and
angular. Accelerations are all angular, however, as
we have already discovered (Sec.
1009.50).
But physics has not been able to coordinate its mathematical
models with the
omnidirectional complexity of the angular acceleration,
so it has used only the linear,
three-dimensional, XYZ, tic-tac-toe grid in measuring
and analyzing its experiments.
Trying to analyze the angular accelerations exclusively
with straight lines, 90-degree
central angles, and no chords involves pi (
Physics thought it had found only two kinds of acceleration:
linear and
angular. Accelerations are all angular, however, as
we have already discovered (Sec.
1009.50).
But physics has not been able to coordinate its mathematical
models with the
omnidirectional complexity of the angular acceleration,
so it has used only the linear,
three-dimensional, XYZ, tic-tac-toe grid in measuring
and analyzing its experiments.
Trying to analyze the angular accelerations exclusively
with straight lines, 90-degree
central angles, and no chords involves pi ( )
and other
irrational constants to correct its
computations, deprived as they are of conceptual models. )
and other
irrational constants to correct its
computations, deprived as they are of conceptual models.
|

|
1032.23
 Critical-proximity crimping-in of local wave coil-spring
contractions of the
Little System by the Big System reveals the local radius
as always a wavilinear short
section of a greater system arc in pure, eternal, generalized
principle.
Critical-proximity crimping-in of local wave coil-spring
contractions of the
Little System by the Big System reveals the local radius
as always a wavilinear short
section of a greater system arc in pure, eternal, generalized
principle.
|
| Next Section: 1032.30 |