1106.00 Inside-Outing of Tetrahedron in Transformational Projection Model
1106.10 Complementary Negative Tetrahedron: The rod ends can be increased beyond the phase that induced the 180-degree triangle, and the vertexes of the steel-spring surface triangle can go on to be increased beyond 180 degrees each, and thus form a negative triangle. This is to say that the original tetrahedron formed between the three vertexes of the spherical triangle on the sphere's surface__with the center of the sphere as the fourth point__will have flattened to one plane when the vertexes are at 180 degrees; at that moment the tetrahedron is a hemisphere. By lengthening the radii again and increasing the triangle's original "interior" angles, the tetrahedron will turn itself inside out. In effect, what seems to be a "small," i.e., an only apparently ``plane" equilateral triangle must always be a small equilateral spherical triangle of a very big sphere, and it is always complemented by the negative triangle completing the balance of the surface of the inherent sphere respective to the three lines and three vertexes of the triangle.
1106.11 No triangular surface is conceivable occurring independently of its inherent sphere, as there is no experimentally demonstrable flat surface plane in Universe reaching outward laterally in all directions to infinity; although this has been illusionarily accepted as "obvious" by historical humanity, it is contradictory to experience. The surface of any system must return to itself in all directions and is most economically successful in doing so as an approximate true sphere that contains the most volume with the least surface. Nature always seeks the most economical solutions__ergo, the sphere is normal to all systems experience and to all experiential, i.e., operational consideration and formulation. The construction of a triangle involves a surface, and a curved surface is most economical and experimentally satisfactory. A sphere is a closed surface, a unitary finite surface. Planes are never finite. Once a triangle is constructed on the surface of a sphere__because a triangle is a boundary line closed upon itself__the finitely closed boundary lines of the triangle automatically divide the unit surface of the sphere into two separate surface areas. Both are bounded by the same three great-circle arcs and their three vertexial links: this is the description of a triangle. Therefore, both areas are true triangles, yet with common edge boundaries. It is impossible to construct one triangle alone. In fact, four triangles are inherent to the oversimplified concept of the construction of "one" triangle. In addition to the two complementary convex surface triangles already noted, there must of necessity be two complementary concave triangles appropriate to them and occupying the reverse, or inside, of the spherical surface. Inasmuch as convex and concave are opposites, one reflectively concentrating radiant energy and the other reflectively diffusing such incident radiation; therefore they cannot be the same. Therefore, a minimum of four triangles is always induced when any one triangle is constructed, and which one is the initiator or inducer of the others is irrelevant. The triangle initiator is an inadvertent but inherent tetrahedron producer; it might be on the inside constructing its triangle on some cosmic sphere, or vice versa.
1106.12 It might be argued that inside and outside are the same, but this is not so. While there is an interminable progression of insides within insides in Experience Universe, there is only one outside comprehensive to all insides. So they are not the same, and the mathematical fact remains that four is the minimum of realizable triangles that may be constructed if any are constructed. But that is not all, for it is also experimentally disclosed that not only does the construction of one triangle on the surface of the sphere divide the total surface into two finite areas each of which is bound by three edges and three angles__ergo, by two triangles__but these triangles are on the surface of a system whose unity of volume was thereby divided into two centrally angled tetrahedra, because the shortest lines on sphere surfaces are great circles, and great circles are always formed on the surface of a sphere by planes going through the center of the sphere, which planes of the three-greatcircle-arc-edged triangle drawn on the surface automatically divide the whole sphere internally into two spherical tetrahedra, each of which has its four triangles__ergo, inscribing one triangle "gets you eight," like it or not. And each of those eight triangles has its inside and outside, wherefore inscribing one triangle, which is the minimum polygon, like "Open Sesame," inadvertently gets you 16 triangles. And that is not all: the sphere on which you scribed is a system and not the whole Universe, and your scribing a triangle on it to stake out your ``little area on Earth" not only became 16 terrestrial triangles but also induced the remainder of Universe outside the system and inside the system to manifest their invisible or nonunitarily conceptual ``minimum inventorying'' of ``the rest of Universe other than Earth,'' each of which micro and macro otherness system integrity has induced an external tetrahedron and an internal tetrahedron, each with 16 triangles for a cosmic total of 64 (see Sec. 401.01).
1106.20 Inside-Outing: Inside-outing means that any one of the four vertexes of the originally considered tetrahedron formed on the transformational projection model's triangle, with its spherical center, has passed through its opposite face. The minima and the maxima of the spherical equiside and -angle triangle formed by the steel springs is seen to be in negative triangular complement to the smallest 60-degree+ triangle. The vertexes of even the maxima or minima are something greater than 60 degrees each__ because no sphere is large enough to be flat__or something less than 300 degrees each.
1106.21 The sphere is at its smallest when the two angles of complement are each degrees on either side of the three-arc boundary, and the minima-maxima of the triangles are halfway out of phase with the occurrence of the minima and maxima of the sphere phases.
1106.22 No sphere large enough for a flat surface to occur is imaginable. This is verified by modern physics' experimentally induced abandonment of the Greeks' definition of a sphere, which absolutely divided Universe into all Universe outside and all Universe inside the sphere, with an absolute surface closure permitting no traffic between the two and making inside self-perpetuating to infinity complex__ergo, the first locally perpetual- motion machine, completely contradicting entropy. Since physics has found no solids or impervious continuums or surfaces, and has found only finitely separate energy quanta, we are compelled operationally to redefine the spheric experience as an aggregate of events approximately equidistant in a high-frequency aggregate in almost all directions from one only approximate event (see Sec. 224.07). Since nature always interrelates in the most economical manner, and since great circles are the shortest distances between points on spheres, and since chords are shorter distances than arcs, then nature must interrelate the spheric aggregated events by the chords, and chords always emerge to converge; ergo, converge convexly around each spheric system vertex; ergo, the sums of the angles around the vertexes of spheric systems never add to 360 degrees. Spheres are high-frequency, geodesic polyhedra (see Sec. 1022.10).
1106.23 Because (a) all radiation has a terminal speed, ergo an inherent limit reach; because (b) the minimum structural system is a tetrahedron; because (c) the unit of energy is the tetrahedron with its six-degrees-of-minimum-freedoms vector edges; because (d) the minimum radiant energy package is one photon; because (e) the minimum polar triangle__ and its tetrahedron's contraction__is limited by the maximum reach of its three interior radii edges of its spherical tetrahedron; and because (f) physics discovered experimentally that the photon is the minimum radiation package; therefore we identify the minimum tetrahedron photon as that with radius = c, which is the speed of light: the tetrahedron edge of the photon becomes unit radius = frequency limit. (See Sec. 541.30.)
1106.24 The transformational projection model coupled with the spheric experience data prove that a finite minima and a finite maxima do exist, because a flat is exclusively unique to the area confined within a triangle's three points. The almost flat occurs at the inflection points between spheric systems' inside-outings and vice versa, as has already been seen at the sphere's minima size; and that at its maxima, the moment of flatness goes beyond approximate flatness as the minima phase satisfies the four-triangle minima momentum of transformation, thus inherently eliminating the paradox of static equilibrium concept of all Universe subdivided into two parts: that inside of a sphere and that outside of it, the first being finite and the latter infinite. The continual transforming from inside out to outside in, finitely, is consistent with dynamic experience.
1106.25 Every great circle plane is inherently two spherical segment tetrahedra of zero altitude, base-to-base.
1106.30 Inside-Outing of Spheres: When our model is in its original condition of having its springs all flat (a dynamic approximation) and in one plane, in which condition all the rods are perpendicular to that plane, the rods may be gathered to a point on the opposite side of the spring-steel strap to that of the first gathering, and thus we see the original sphere turned inside out. This occurs as a sphere of second center, which, if time were involved, could be the progressive point of the observer and therefore no "different" point.
1106.31 Considering Universe at minimum unity of two, two spheres could then seem to be inherent in our model. The half-out-of-phaseness of the sphere maxima and minima, with the maxima-minima of the surface triangles, find the second sphere's phase of maxima in coincidence with the first's minima. As the two overlap, the flat phase of the degree triangles of the one sphere's minima phase is the flat phase of the other sphere's maxima. The maxima sphere and the minima sphere, both inside-outing, tend to shuttle on the same polar axis, one of whose smaller polar triangles may become involutional while the other becomes evolutional as the common radii of the two polar tetrahedra refuse convergence at the central sphere. We have learned elsewhere (see Sec. 517) that two or more lines cannot go through the same point at the same time; thus the common radii of the two polar tetrahedra must twistingly avert central convergence, thus accomplishing central core involutional-evolutional, outside-inside-outside, cyclically transformative travel such as is manifest in electromagnetic fields. All of this is implicit in the projection model's transformational phases. There is also disclosed here the possible intertransformative mechanism of the interpulsating binary stars.
1107.00 Transformational Projection Model with Rubber-Band Grid
1107.10 Construction: Again returning the model to the condition of approximate dynamic inflection at maxima-minima of the triangle__i.e., to their approximately flat phase of "one" most-obvious triangle of flat spring-steel strips__in which condition the rods are all perpendicular to the surface plane of the triangle and are parallel to one another in three vertical planes of rod rows in respect to the triangle's plane. At this phase, we apply a rubber-band grid of three-way crossings. We may consider the rubber bands of ideal uniformity of cross section and chemical composition, in such a manner as to stretch them mildly in leading them across the triangle surface between the points uniformly spaced in rows, along the spring-steel strap's midsurface line through each of which the rods were perpendicularly inserted. The rubber bands are stretched in such a manner that each rubber band leads from a point distant from its respective primary vertex of the triangle to a point on the nearest adjacent edge, that is, the edge diverging from the same nearest vertex, this second point being double the distance along its edge from the vertex that the first taken point is along its first considered edge. Assuming no catenary sag or drift, the "ideal" rubber bands of no weight then become the shortest distances between the edge points so described. Every such possible connection is established, and all the tensed, straight rubber bands will lie in one plane because, at the time, the springs are flat__and that one plane is the surface of the main spring-steel triangle of the model.
1107.11 The rubber bands will be strung in such a way that every point along the steel triangle mid-edge line penetrated by the rods shall act as an origin, and every second point shall become also the recipient for such a linking as was described above, because each side feeds to the other sides. The "feeds" must be shared at a rate of one goes into two. Each recipient point receives two lines and also originates one; therefore, along each edge, every point is originating or feeding one vertical connector, while every other, or every second point receives two obliquely impinging connector lines in addition to originating one approximately vertically fed line of connection.

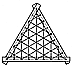Fig. 1107.12 		1107.12 The edge pattern, then, is one of uniform module divisions separated by points established by alternating convergences with it: first, the convergence of one connector line; then, the convergence of three connector lines; and repeat.
1107.13 This linking of the three sides will provide a rubber-band grid of three-way crossings of equi-side and -angle triangular interstices, except along the edges of the main equiangle triangle formed by the spring-steel pieces, where half-equilateral triangles will occur, as the outer steel triangle edges run concurrently through vertexes to and through midpoints of opposite sides, and thence through the next opposite vertexes again of each of the triangular interstices of the rubber-band grid interacting with the steel edges of the main triangle.
1107.14 The rubber-band, three-way, triangular subgridding of the equimodule spring-steel straps can also be accomplished by bands stretched approximately parallel to the steel-strap triangle's edges, connecting the respective modular subdivisions of the main steel triangle. In this case, the rubber-band crossings internal to the steel-band triangle may be treated as is described in respect to the main triangle subtriangular gridding by rubber bands perpendicular to the sides.
1107.20 Transformation: Aggregation of Additional Rods: More steel rods (in addition to those inserted perpendicularly through the steel-band edges of the basic triangle model) may now be inserted__also perpendicularly__through a set of steel grommets attached at (and centrally piercing through) each of the points of the three-way crossings of the rubber bands (internal to the big triangle of steel) in such a manner that the additional rods thus inserted through the points of three-way crossings are each perpendicular to the now flat-plane phase of the big basic articulatable steel triangle, and therefore perpendicular to, and coincident with, each of the lines crossing within the big steel triangle face. The whole aggregate of rods, both at edges and at internal intersections, will now be parallel to one another in the three unique sets of parallel planes that intersect each other at 60 degrees of convergence. The lines of the intersecting planes coincide with the axes of the rods; i.e., the planes are perpendicular to the plane of the basic steel triangle and the lines of their mutual intersections are all perpendicular to the basic plane and each corresponds to the axis of one of the rods. The whole forms a pattern of triangularly bundled, equiangular, equilateral-sectioned, parallel-prism-shaped tube spaces.

Fig. 1107.21 		1107.21 Let us now gather together all the equally down-extending lengths of rod ends to one point. The Greeks defined a sphere as a surface equidistant in all directions from one point. All the points where the rods penetrate the steel triangle edges or the three-way-intersecting elastic rubber-band grid will be equidistant from one common central point to which the rod ends are gathered__and thus they all occur in a spherical, triangular portion of the surface of a common sphere__specifically, within the lesser surfaced of the two spherical triangles upon that sphere described by the steel arcs. Throughout the transformation, all the rods continue their respective perpendicularities to their respective interactions of the three-way crossings of the flexible grid lines of the basic steel triangle's inherently completable surface.
1107.22 If the frequency of uniform spacing of the perpendicularly__and equidistantly__penetrating and extending rods is exquisitely multiplied, and the uniform intervals are thus exquisitely shortened, then when the rod ends are gathered to a common point opposite either end of the basic articulatable steel-band triangle, the gathered ends will be closer together than their previous supposedly infinitely close parallel positioning had permitted, and the opposite ends will be reciprocally thinned out beyond their previous supposedly infinite disposition. Both ends of the rods are in finite condition__ beyond infinite__and the parallel phase (often thought of as infinite) is seen to be an inflection phase between two phases of the gathering of the ends, alternately, to one or the other of the two spherical centers. The two spherical centers are opposite either the inflection or flat phase of the articulating triangle faces of the basic articulatable triangle of our geodesics transformational projection model.
Next Section: 1107.30
Copyright © 1997 Estate of R. Buckminster Fuller