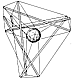
Fig. 401.00 		401.00 Twelve Vectors of Restraint, Six Positive and Six Negative, Define Minimum System

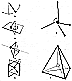Fig. 401.01 		401.01 At the top of Illus. 401.01 (see also Illus. 401.00 in drawings section), we see something like a ping-pong ball attached to a string. The pingpong ball represents me, and the string is gravity (or mass attraction), with its other end tethered to a point that represents all the rest of Universe that isn't me. Because of mass attraction, the one thing that I cannot do is escape absolutely from Universe. I may try to exert terrific acceleration and shoot out through a hole in the Galaxies, beyond the Pleiades, where the stars seemingly are so scarce that as I look back from fantastically far out, all the stars of Universe seem to be collected in approximately one bright spot. The single string of the model, long though it may be, represents the combined mass attraction exerted upon me by all the stars of Universe.
401.02 Tetherball: There is an old game called tetherball, played by tennis players lacking a tennis court. There is a tennis ball fastened powerfully to a strong, slender cord 19 feet long suspended from the top of a pole 22 feet in height above the ground level. There is a circular marker on the pole at the 11' 4" height. The server bats the ball in a clockwise circumferential direction around the pole, attempting to wind its cord completely around the pole above the 11' 4" mark. The opponent can intercept and attempt to wind the ball counterclockwise. Obviously, a tethered ball on a long string is free to describe any omnigeometric forms of circles, spheres, or giraffes, but it cannot get away from the Universe. This is called one restraint: the fundamental "otherness" essential to initial "awareness" of the observer. (Nothing to observe: no awareness: only nothingness.) Otherness always imposes a minimum of one restraint, weak though it may be, on all awareness, which is the beginning of "Life."
401.03 But the imagined experience of cosmically long journeys teaches me that the possibility of finding such a hole in the celestial myriadicity to attain such a unified paralactic bunching of all island nebulae is a futile search. Therefore, I resign myself to acknowledgment of at least two a priori restraints that inescapably affect my relative cosmic freedom. Hoping to save myself vast cosmic time, and accepting my present position in Universe, I try to process the known data on the mass dimensions of all the known stars and try to divide them all into two opposite hemispherical teams__those to my right and those to my left. Then assuming all the right-hand hemisphere group's mass attraction to be accumulatively resolved into one mass-attractive restraint tied to my right arm's wrist, and all the other cosmic hemisphere's equal tensions tied to my left arm's wrist, I find myself used like a middleman in a ropeless tug of war, liable to have my arms pulled out of my armpits. So I tie both the tension lines around my waist. Now I am in the same dynamic situation as a ping-pong ball suspended in the middle of a one-string fiddle. Because all strings, no matter how tautly strung, can still vibrate, I can still move. But I find that with two restraints I can move about in circles, cloverleafs, or figures-of-eight, but always and only in a plane that is perpendicular to the string of which I am in the middle.
401.04 Now I conclude that the various motions of the stars make it illogical to assume any persistence of the two hemispherical star sphere groupings. The star accelerations produce the inertial advantage of awayness to which my mass-attraction tethers were attached. I therefore conclude that it is more probable that such dynamic inertia will persist in three groups. Now I have three restraints, and the ping-pong ball "me" acts as if it were in the middle of a drumhead, or as tensilely suspended at the center of area of a triangle by three strings fastened at the triangle's corners. The ping-pong ball "me" can still move, but only in a line perpendicular to the plane of the drumhead or web triangle. I am constrained by three converging lines as I oscillate to and fro between the opposite apexes of two dynamically described, base-to-base, positive or negative tetrahedra formed by the resonating drumhead's terminal oscillations.

Fig. 401.05 		401.05 With only one restraint, the ball was moving omnidirectionally or multidimensionally. With two restraints, it was moving in a plane; with three restraints, it moves only in a line. I now conclude that it is more probable that I can concentrate all the restraints operating upon me from all the stars because of the multidirectional pull of all the stars actually pulling me. I conclude that there is much redundancy but that four restraints is closer to a matter of reality than three restraints. When we attach a fourth restraint perpendicular to the center of the drumhead and pull it only in the "fro" direction, the ping-pong ball "me" seems at last to be immobilized. With four restraints the ping- pong ball "me" can no longer move either toward or away from any other parts of the Universe. But the ball can twist locally, that is, it can rotate in place around an axis, and that axis itself can incline at many angles, as does the gyroscope top, without alteration of its volumetric center position in respect to the four vertexial star groups. Because the vectors are coming together in nonequilateral quadrangles, i.e., in trapeoids, the restraints are not intertriangulated, and we have learned experimentally that only triangles are stable. (See Sec. 610, Triangulation.) Therefore, it is possible for the ball to "turbine," rotate, and precess locally in place without altering the geometrical position at volume center of the celestial tetrahedron from whose four corners the four vectors of restraint were imposed. The six edges of the celestial spherical tetrahedron represent the three mass-attraction restraints imposed on each of the tetrahedron's four corner mass centers as each being in normal acceleration is precessionally restrained from exiting from Universe. Each of the four corners' group massiveness is restrained by all three of the other tetrahedral corner mass centers. Any one of the massmoment acceleration tendencies to part company with the others is overpowered three-to-one by the three others. Thus the cohering integrity of Universe is manifest to us by consideration of the celestial advantage points from which our four central restraints were mounted. Though the ping-pong "me" ball can be twisted and torqued in place, it cannot be moved from its tetrahedral center position. To prevent local in-position twist and torque, each of the four corner tensional restraints will have to be multiplyingly replaced by three restraints, all springing from three external points at each of the four tetrahedral corners; and each of the three tensions from any one of the four corners must cross the others triangularly and be attached tangentially to the ball at the center. These 12 now completely restrain any motion of the central ball in relation to the other four.
401.06 The purpose of our investigation was to find the requirements of a minimum system. Our experimental model demonstrates that it takes four vectors to define a point with the ping-pong ball at the center of gravity and center of volume of the regular tetrahedron. It takes 12 such vectors to both position and locally immobilize. It takes six external push vectors and six external pull vectors to define the minimum nuclear structural system: a primary subdivision of Universe. To summarize, the celestial tetrahedron has six positive and six negative internal vectors and six positive and six negative external vectors.
401.07 Four external "star" foci effecting complete immobilization of the "me" ball are the same four event foci that we learned earlier (Sec. 405.05) always constitute the minimum number of events necessary to define the insideness and outsideness of a system.
401.08 Tetherball: In the "me" ball in Universe 12 structural restraints are necessary to eliminate all the degrees of freedom because all the initial four restraints are connected to the surface of the "me" sphere and not to its center. The four points of tangency describe a square, and they permit local twist and torque because a square is unstable. So each tension has to be replaced by three tension restraints to produce a tensegrity structure within which the "me" ball may be omninonredundantly immobilized.
402.00 Tetrahedron as System
402.01 The tetrahedron as a real system consists of one concave tetrahedron and a second convex tetrahedron, plus a third tetrahedron for all the Universe outside the system-as-tetrahedron, and a fourth tetrahedron complementarily accounting for all Universe inside the system-as-tetrahedron. All the angles are the same on the inside as on the outside.
402.02 A tetrahedron is a triangularly faceted polyhedron of four faces. It is unique as a system, for it is the minimum possible system.
403.00 Stable and Unstable Systems
403.01 There are stable systems and unstable systems. (For a discussion of stable and unstable structures, see Sec. 608, Stability: Necklace.)
403.02 Conceptuality: Unstable systems are conceptual as momentary positional relationships of unstructured-component event aggregates; for example, amongst the stars comprising the Big Dipper__in Ursa Major__the second and third stars in the dipper's handle are, respectively, 100- and 200-light-years away from Earth and, though seemingly to us in the same plane, are not all so; and they are both moving in opposite directions and so in due course they will no longer seem to be in the same constellation. In the same way, four airplanes flying in different directions may be within visible range of one another, but are far too remote for mass inter-attraction to become critical and pull them into one another. Stable systems are conceptual as structured, which means componently omni- mtertriangulated critical-proximity, interrelevant, coordinate, constellar event aggregates.
403.03 Generalized Principles: If the only momentary and optically illusory system consideration proves to be unstable, it does not manifest generalized principle. If systems are stable, they are inherent in and accommodate all generalized principles.
Next Section: 410.00
Copyright © 1997 Estate of R. Buckminster Fuller