Organics: It could be that organic chemistries do
not require nuclei.
|
|
415.20
Organics: It could be that organic chemistries do
not require nuclei.
|
|
|
415.21
The first closest-packed, omnitriangulated, ergo structurally
stabilized, but
non-nuclear, equiradius-sphered, cubical agglomeration
has 14 spheres. This may be
Carbon 14, which is the initially closest-packed, omnisymmetrical,
polyhedral
fourteenness, providing further closest-packability
surface nests suitable for structurally
mounting hydrogen atoms to produce all organic matter.
|
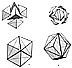 Fig. 415.22 |
415.22
The cube is the prime minimum omnisymmetrical allspace
filler. But the cube
is nonstructural until its six square faces are triangularly
diagonaled. When thus
triangularly diagonaled, it consists of one tetrahedron
with four one-eighth octahedra, of
three isosceles and one equilateral-faced tetrahedron,
outwardly applied to the nuclear
equilateral tetrahedron's four triangular faces. Thus
structurally constituted, the
superficially faced cube is prone to closest-packing
self-associability. In order to serve as
the carbon ring (with its six-sidedness), the cube of
14 spheres (with its six faces) could be
joined with six other cubes by single atoms nestable
in its six square face centers, which
singleness of sphericity linkage potential is providable
by Hydrogen 1.
|
|
|
415.23
In the atoms, we are always dealing in equiradius
spheres. Chemical
compounds may, and often do, consist of atomic spheres
with a variety of radial
dimensions. Since each chemical element's atoms are
characterized by unique frequencies,
and unique frequencies impose unique radial symmetries,
this variety of radial
dimensionality constitutes one prime difference between
nuclear physics and chemistry.
|
|
|
415.30
Eight New Nuclei at Fifth Frequency of Vector Equilibrium:
Frequency
five embraces nine nuclei: the original central nucleus
plus eight new nuclei occurring at
the centers of volume of the eight tetrahedra symmetrically
surrounding the nucleus, with
each of the nine enclosed with a minimum of two layers
of spheres.
|
|
|
415.31
The vector equilibrium at f 0 = 12;
at f 2 = 42; f 3
= 92; f 4 = 162 spheres in the
outer shell; and at f 5 = 252 we get eight new nuclei.
Therefore, their eightness of
"begetness" relates to the eight triangles of the vector
equilibrium.
|
|
|
415.32
Six nucleated octahedra with two layer omni-enclosure
of their nuclei does
not occur until f 6 = 362 in the outer shell of the vector
equilibrium. At this stage we have
six new nuclei, with 14 nuclei surrounding the 15th,
or original, nucleus.
|
|
|
415.40
Begetted Eightness: The "begetted" eightness as the
system-limit number of
nuclear uniqueness of self-regenerative symmetrical
growth may well account for the
fundamental octave of unique interpermutative integer
effects identified as plus one, plus
two, plus three, plus four, as the interpermutated effects
of the integers one, two, three,
and four, respectively; and as minus four, minus three,
minus two, minus one,
characterizing the integers five, six, seven, and eight,
respectively. The integer nine always
has a neutral, or zero, intermutative effect on the
other integers. This permutative,
synergetic or interamplifying or dimensioning effect
of integers upon integers, together
with the octave interinsulative accommodation produced
by the zero effect of the
nineness, is discussed experientially in our section
on Indigs in Chapter 12, Numerology.
|
|
|
415.41
The regenerative initial eightness of first-occurring
potential nuclei at the
frequency-four layer and its frequency-five confirmation
of those eight as constituting true
nuclei, suggest identity with the third and fourth periods
of the Periodic Table of Chemical
Elements, which occur as
|
|
|
415.42
Starting with the center of the nucleus: plus one,
plus two, plus three, plus
four, outwardly into the last layer of nuclear uniqueness,
whereafter the next pulsation
becomes the minus fourness of the outer layer (fifth
action); the sixth event is the minus
threeness of canceling out the third layer; the seventh
event is the minus twoness canceling
out the second layer; thc eighth event is the minus
oneness returning to the center of the
nucleus__ all of which may be identified with the frequency
pulsations of nuclear systems.
|
|
|
415.43
The None or Nineness/Noneness permits wave frequency
propagation
cessation. The Nineness/Zeroness becomes a shutoff valve.
The Zero/Nineness provides
the number logic to account for the differential between
potential and kinetic energy. The
Nineness/Zeroness becomes the number identity of vector
equilibrium, that is, energy
differentiation at zero. (See Secs.
1230 et seq. and
the Scheherazade Number.)
|
|
|
415.44
The eightness being nucleic may also relate to the
relative abundance of
isotopal magic numbers, which read 2, 8, 20, 50, 82,
126....
|
|
|
415.45
The inherent zero-disconnectedness accounts for the
finite energy packaging
and discontinuity of Universe. The vector equilibria
are the empty set tetrahedra of
Universe, i.e., the tetrahedron, being the minimum structural
system of Universe
independent of size, its four facet planes are at maximum
remoteness from their opposite
vertexes and may have volume content of the third power
of the linear frequency. Whereas
in the vector equilibrium all four planes of the tetrahedra
pass through the same opposite
vertex__which is the nuclear vertex__and have no volume,
frequency being zero: F0.
|
|
|
415.50
Vector-Equilibrium Closest-Packing Configurations:
The vector
equilibrium has four unique sets of axes of symmetry:
|
|
|
415.51
Consequently, the (no-nucleus-accommodating) icosahedron
formed of
equiradius, triangularly closest-packed spheres occurs
only as a one-sphere-thick shell of
any frequency only. While the icosahedron cannot accommodate
omnidirectionally closest-
packed multishell growth, it can be extended from any
one of its triangular faces by
closest-packed sphere agglomerations. Two icosahedra
can be face-bonded.
|
|
|
415.52
The icosahedron has three unique sets of axes of symmetry:
|
|
|
415.53
While the 15-axes set and the 6-axes set of the icosahedron
are always
angularly askew from the vector equilibrium's four out
of its 10 axes of symmetry are
parallel to the set of four axes of symmetry of the
vector equilibrium. Therefore, the
icosahedron may be face-extended to produce chain patterns
conforming to the
tetrahedron, octahedron, vector equilibrium, and rhombic
dodecahedron in
omnidirectional, closest-packing coordination__ but only
as chains; for instance, as open
linear models of the octahedron's edges, etc.
|
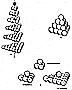 Fig. 415.55 |
415.55
Nucleus and Nestable Configurations in Tetrahedra:
In any number of
successive planar layers of tetrahedrally organized
sphere packings, every third triangular
layer has a sphere at its centroid (nucleus). The dark
ball rests in the valley between three
balls, where it naturally falls most compactly and comfortably.
The next layer is three balls
to the edge, which means two-frequency. There are six
balls in the third layer, and there
very clearly is a nest right in the middle. There are
ten balls in the fourth layer: but we
cannot nest a ball in the middle because it is already
occupied by a dark centroid ball.
Suddenly the pattern changes, and it is no longer nestable.
|
|
|
415.56
At first, we have a dark ball at the top; then a second
layer of three balls with
a nest but no nucleus. The third layer with six balls
has a nest but no nucleus. The fourth
layer with ten balls has a dark centroid ball at the
nucleus but no nestable position in the
middle. The fifth layer (five balls to the edge; four
frequency) has 15 balls with a nest
again, but no nucleus. This 35 sphere tetrahedron with
five spheres on each edge is the
lowest frequency tetrahedron system that has a central
sphere or nucleus. (See Fig. A,
illustration 415.55.)
|
|
|
415.57
The three-frequency tetrahedron is the highest frequency
singlelayer, closest-
packed sphere shell without a nuclear sphere. This three-frequency,
20-sphere, empty, or
nonsphere nucleated, tetrahedron may be enclosed by
an additional shell of 100 balls; and
a next layer of 244 balls totaling 364, and so on. (See
Fig. B, illustration 415.55.)
|
|
|
415.58
Basic Nestable Configurations: There are three basic
nestable possibilities
shown in Fig. C. They are (1) the regular tetrahedron
of four spheres; (2) the one-eighth
octahedron of seven spheres; and (3) the quarter tetrahedron,
with a 16th sphere nesting
on a planar layer of 15 spheres. Note that this "nesting"
is only possible on triangular
arrays that have no sphere at their respective centroids.
This series is a prime hierarchy.
One sphere on three is the first possibility with a
central nest available. One sphere on six
is the next possibility with an empty central nest available.
One sphere on 10 is impossible
as a ball is already occupying the geometrical center.
The next possibility is one on 15 with
a central empty nest available.
|
|
|
415.59
Note that the 20-ball empty set (see Fig. B, illustration
415.55) consists of
five sets of four-ball simplest tetrahedra and can be
assembled from five separate
tetrahedra. The illustration shows four four-ball tetrahedra
at the vertexes colored
"white." The fifth four-ball tetrahedron is dark colored
and occupies the central octahedral
space in an inverted position. In this arrangement,
the four dark balls of the inverted
central tetrahedron appear as center balls in each of
the four 10-ball tetrahedral faces.
|
| Next Section: 416.00 |