Absolute Four and Octave Wave
|
|
1222.00
Absolute Four and Octave Wave
|
|
|
1222.10
Prime Dichotomy: It is found that all decimally expressed
whole numbers
integrate into only nine digits. Looking at the charts
(Indig Table B), we see the nine
indigs resultant to the decimal system, or congruence
in modulo ten, have integrated
further to disclose only nine unique operational effects
upon all other integers. These nine
interoperational effects in turn reduce into only eight
other integer-magnitude-altering
effects and one no-magnitude-altering effect. The "octave"
of eight magnitude-altering sets
of indigs in turn disclose primary dichotomy into four
positively altering and four
negatively altering magnitude operators, with each set
arranged in absolute arithmetical
sequence of from one to four only.
|
|
|
1222.11
Indig congruences demonstrate that nine is zero and
that number system is
inherently octave and corresponds to the four positive
and four negative octants of the
two polar domains (obverse and reverse) of the octahedron__and
of all systems__which
systematic polyhedral octantation limits also govern
the eight 45-degree-angle constituent
limits of 360-degree unity in the trigonometric function
calculations.
|
|
|
1222.12
The inherent + 4, - 4, 0, + 4,__4,
0  of number also
corresponds (a) to the
four varisized spheres integrating tritangentially to
form the tetrahedron (see Sec.
1222.20
and (b) to the octantation of the Coupler (see Sec.
954.20 954.20) by its eight allspace-
filling Mites (AAB Modules) which, being inherently
plus-or-minus biased, though
superficially invariant (i.e., are conformationally
identical); altogether provide lucidly
synergetic integration (at a kindergarten-comprehendible
level) of cosmically basic number
behavior, quantum mechanics, synergetics, nuclear physics,
wave phenomena in general,
and topologically rational accountability of experience
in general.
|
|
|
1222.20
Cosmically Absolute Numbers: There are apparently no
cosmically
absolute numbers other than 1, 2, 3, and 4. This primitive
foumess identifies exactly with
one quantum of energy and with the foumess of the tetrahedron's
primitive structuring as
constituting the "prime structural system of Universe,"
i.e., as the minimum
omnitriangulated differentiator of Universe into insideness
and outsideness, which alone,
of all macro-micro Universe differentiators, pulsates
inside-outingly and vice verse as
instigated by only one force vector impinging upon it.
(See Sec.
624.)
|
|
|
1222.30
Casting Out Nines: We can use any congruence we like,
and the pattern
will be the same. The wave phenomenon, increasing by
four and decreasing by four, is an
octave beginning and ending at zero. From this I saw
that nine is zero.
|
|
|
1222.31
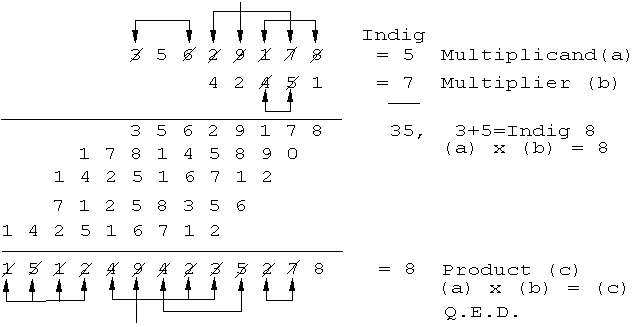
When I worked for Armour and Company before World War
I, I had to add
and multiply enormous columns of figures every day.
As yet, neither commercially
available adding machines nor electric calculators existed.
The auditors showed us how to
check our multiplications by "casting out nines." This
is done by inspecting all the input
integers of multiplication, first crossing out any nines
and then crossing out any
combinations of integers that add to nine, exclusively
within either the (a) multiplicands,
(b) multipliers, or (c) products of multiplication,
taken separately. This means we do not
take combinations of integers occurring in other than
their own respective (a), (b), or (c)
sets of integers that add up to nine.
|
|
|
1222.32
|
|
|
1223.00
Wave Pulsation of Indigs
|
|
|
1223.10
Pulsative Octave: The interaction of all numbers other
than nine creates the
wave phenomenon described, i.e., the self-invertible,
self-inside-outable octave increasing
and decreasing pulsatively, fourfoldedly, and tetrahedrally.
No matter how complex a
number-aggregating sequence of events and conditions
may be, this same number behavior
phenomenon is all that ever happens. There is thus a
primitively comprehensive,
isotropically distributive, carrier-wave order omniaccommodatively
permeating and
embracing all phenomena. (See Sec.
1012.10)
|
|
|
1223.11
As the nine columns of Indig Table 2 show, I have integrated
the digits of all
the different multiplication systems and have always
found the positively-negatively
pulsative, octave, zero-nine-intervaled, ergo interference-free,
carrier-wave pattern to be
permeating all of them in four alternative interger-mix
sequences; with again, four
positively ordered and four negatively ordered sequence
sets, all octavely ventilated by
zero nines cyclically, ergo inherently, ergo eternally
synchronized to non-inter-
interferences.
|
 Fig. 1223.12 |
1223.12
As will also be seen in Indig Table 2, the integer
carrier waves can pulse in
single sets, as in Columns 1 and 8; in double pairs,
as in Columns 4 and 5; in triple triplets,
as in Columns 3 and 6; and in double quadruplets, as
in Columns 2 and 7__always
octavely interspersed with zeros and, in the case of
Columns 3 and 6, interspersed with
zeros triangularly as well as octavely. This also means
that the omnidirectional wave
interpermutatings are accommodated as points or as lines;
or as triangular areas; or as
tetrahedral volumes__both positive and negative.
|
|
|
1223.13
Thus we are informed that the carrier waves and their
internal-external zero
intervalling are congruent with the omnitriangulated,
tetraplaned, four-dimensional vector
equilibria and the omniregenerative isotropic matrix
whose univectorings accommodate
any wavelength or frequency multiplying in respect to
any convergently-divergently
nuclear system loci of Universe.
|
|
|
1223.14
Not only is there an external zero intervalling between
all the unique octave-
patterning sets in every one of the four positive, four
negative systems manifest, but we
find also the wave-intermodulating indigs within each
octave always integrating sum-
totally internally to the octaves themselves as nines,
which is again an internal zero
content__this produces in effect a positive zero function
vs. a negative zero function, i.e.,
an inside-out and outside-out zero as the ultracosmic
zero-wave pulsativeness.2
(Footnote 2: See Sec. 1012, which describes a closest-sphere-packing model of the same phenomenon. If we make an X configuration with one ball in the center common to both triangles of the X, the ball at the intersection common to both represents the zero__or the place where the waves can pass through each other. The zero always accomodates when two waves come together. We know that atoms close-pack in this manner, and we know how wave phenomena such as radio waves behave. And now we have a model to explain how they do not interfere.) |
|
|
1223.15
Thus we discover the modus operandi by which radio
waves and other
waves pass uninterferingly through seeming solids, which
are themselves only wave
complexes. The lack of interference is explained by
the crossing of the high-frequency
waves through the much lower-frequency waves at the
noninterfering zero points, or
indeed by the varifrequencied waves through both one
another's internal and external zero
intervals. (See Illus.
1012.13A and B.)
|
|
|
1223.16
If the readers would like to do some of their own indig
exploration they may
be instructively intrigued by taking a book of mathematical
tables and turning to the table
of second powers of integers. If they undertake to indig
each of those successively listed
second-power numbers they will discover that, for the
first 100 numbers listed, a unique
sequence of 24 integers will appear that peaks at 25,
reverses itself, and bottoms at one,
only to turn again and peak at 50, bottom at 75, and
peak again at the 100th number
which, when analyzed, manifests a 2 × 2 × 2 = 8 = 23
× 3 = 24 four-dimensional wave.
This four-dimensional wave is only comprehendible when
we discover (see Sec.
982.62)
the three-frequency reality of F3 × 2 l/2, 3, 4, 5,
6, the a priori, initially-volumed, ergo
three-dimensional reality multiplied by the third power
of omnidirectional growth rate.
|
|
|
1224.00
Wave Pulsation of Number 24
|
|
|
1224.10
Vector Equilibrium and Octave Wave
|
|
|
1224.11
The second powering of numbers apparently involves
a 24-positive and 24-
negative resonance phasing. The potential variables
of the indigs of the second-powering
of the 24 successive integers running between 0 and
25, and indigs of the 24 integers
descending successively between 25 and 50, and repeating
the 24 integers between 50 and
75, and the 24 integers between 75 and 100 ad infinitum,
apparently account for all the
equilibrious-disequilibrious, radiational-gravitational,
convergent-divergent,
curviwavilinear behaviors in respect to the vector equilibrium
as well as for the unique
rates of growth or contraction of closest-packed-spherical
agglomerating.
|
|
|
1224.12
In respect to the progressive series of n2 product
numbers as expressed in
congruence-in-modulo- 10, a unique 24-integer series
of terminal, submodulus-10, excess
integers completes its series direction with 24 and
makes its verse-and-reverse series at the
common hinges of 252, 752, 1002 in increments of +24,
-24, +24, -24, or in a positively
occurring, three-octave-wave increment sequence followed
each time by a reversely
occurring, three-octave-wave, unique harmonic theme.
|
|
|
1224.13
The three-octave, 24-integer series is manifest in
the convergent-divergent,
tetrahedral wave propagations of the vector equilibrium
wherein the eight tetrahedra share
their nuclear sphere and then share their common apex
spheres as they embrace that
nuclear sphere by expanding in successive triangular
closest-packed sphere layers.
(Compare Secs.
1012.11
and
1033.030.)
|
|
|
1224.14
The lines omniinterconnecting the sphere centers of
those successively
embracing layers produce equiangular triangles, or electromagnetic
fields, the sum of
whose areas in each successive layer is always n2 of
the number in each series in that layer.
In contradistinction to the triangular field, in the
series of triangularly closest-packed
sphere layers, every two adjacent layers' series produces
the next greater n2 number of
spheres, with the number of closest-packed sphere triangles
in the waxing and waning
phases of the series being governed by the frequency
of the wave propagation elected for
consideration in each instant.
|
|
|
1224.20
Recapitulation
|
|
|
1224.21
The interwave and intervolumetric behavior of the number
24 may be
considered variously as follows:
|
|
|
1224.30
Turnaround Terminals
|
|
|
1224.31
The powerful 24-ness number behavior with its great-circle
congruences and
three-octave harmonics may have significant ramifications
embracing the unique
frequencies of the chemical compoundings as well as
the nuclear geometry elucidated
elsewhere in this work. (Sec.
1033
passim.) The terminal-suffix
excess integers of the
series of second powers of numbers as expressed in congruence
in modulo-10 displays the
sequence of uniquely aberrating eccentricities in respect
to the whole 24-integer phrases.
|
|
|
1224.32
The large figure "2"' in the last column of the Indig
Table (Fig.
1223.12B)
shows that the terminal digits of the second powers
of numbers turn around at the
middling number 25.
|
|
|
1224.33
There are 24 positive and 24 negative unique numbers
that reverse
themselves between 0 and 50. This reflects three positive
and three negative octaves with
turnaround terminal zero accommodation.
|
|
|
1224.34
The "square" identifies that number of energy units
occurring in the outer
shell of all nuclear phenomena with the second-powering
characteristic being that of both
the gravitation and the radiational constant's surface
growth.
|
1230.00
Scheherazade Numbers
|
|
1230.10
Prime-Number Accommodation: Integration of Seven: The
Babylonians did
not accommodate a prime number like 7 in their mathematics.
Plato had apparently been
excited by this deficiency, so he multiplied 360 by
7 and obtained 2,520. And then, seeing
that there were always positives and negatives, he multiplied
2,520 by 2 and obtained
5,040. Plato apparently intuited the significance of
the number 5,040, but he did not say
why he did. I am sure he was trying to integrate 7 to
evolve a comprehensively rational
circular dividend.
|
|
|
1230.11
H2O is a simple low number. As both chemistry and quantum
physics show,
nature does all her associating and disassociating in
whole rational numbers. Humans
accommodated the primes 1, 2, 3, and 5 in the decimal
and duodecimal systems. But they
left out 7. After 7, the next two primes are 11 and
13 . Humans' superstition considers the
numbers 7, 11, and 13 to be bad luck. In playing dice,
7 and 11 are "crapping" or drop-out
numbers. And 13 is awful. But so long as the comprehensive
cyclic dividend fails to
contain prime numbers which may occur in the data to
be coped with, irrational numbers
will build up or erode the processing numbers to produce
irrational, ergo unnatural,
results. We must therefore realize that the tables of
the trigonometric functions include the
first 15 primes 1, 2, 3, 5, 7, 11, 13, 17, 19, 23,29,31,41,43.
|
|
|
1230.12
We know 7 × 11 is 77. If we multiply 77 by 13, we get
1,001. Were there
not 1,001 Tales of the Arabian Nights? We find these
numbers always involved with the
mystical. The number 1,001 majors in the name of the
storytelling done by Scheherazade
to postpone her death in the Thousand and One Nights.
The number 1,001 is a binomial
reflection pattern: one, zero, zero, one.
|
|
|
1230.20
SSRCD Numbers: If we multiply the first four primes,
we get 30. If we
multiply 30 times 7, 11, and 13, we have 30 × 1,001
or 30,030, and we have used the first
seven primes.
|
|
|
1230.21
We can be intuitive about the eighth prime since the
octave seems to be so
important. The eighth prime is 17, and if we multiply
30,030 by 17, we arrive at a
fantastically simple number: 510,510. This is what I
call an SSRCD Number, which stands
for Scheherazade Sublimely Rememberable Comprehensive
Dividend. As an example we
can readily remember the first
eight primes factorial__510,510!
(Factorial means
successively multiplied by themselves, ergo 1 × 2 ×
3 × 5 × 7 × 11 × 13 × 17= 510,510.)
|
|
|
1230.30
Origin of Scheherazade Myth: I think the Arabian priest-mathematicians
and their Indian Ocean navigator ancestors knew that
the binomial effect of 1,001 upon
the first four prime numbers 1, 2, 3, and 5 did indeed
provide comprehensive dividend
accommodation of all the permutative possibilities of
all the ''story-telling-taling-tallying,"
or computational systems of the octave system of integers.
|
|
|
1230.31
The function of the grand vizier to the ruler was that
of mathematical
wizard, the wiz of wiz-dom; and the wiz-ard kept secret
to himself the mathematical
navigational ability to go to faraway strange places
where he alone knew there existed
physical resources different from any of those occurring
''at home," then voyaging to
places that only the navigator-priest knew how to reach,
he was able to bring back
guaranteed strange objects that were exhibited by the
ruler to his people as miracles
obviously producible only by the ruler who secretly
and carefully guarded his vizier's
miraculous power of wiz-dom.
|
|
|
1230.32
To guarantee their own security and advantage, the
Mesopotamian
mathematicians, who were the overland-and-overseas navigator-priests,
deliberately hid
their knowledge, their mathematical tools and operational
principles such as the
mathematical significance of 7 × 11 × 13 = 1,001 from
both their rulers and the people.
They used psychology as well as outright lies, combining
the bad-luck myth of the three
prime integers with the mysterious inclusiveness of
the Thousand and One Nights. The
priests warned that bad luck would befall anyone caught
using 7s, 11s, or 13s.
|
|
|
1230.33
Some calculation could only be done by the abacus or
by positioning
numbers. With almost no one other than the high priests
able to do any calculation, there
was not much chance that anyone would discover that
the product of 7, 11, and 13 is
001, but "just in case," they developed the diverting
myth of Scheherazade and her
postponement of execution by her Thousand and One Nights.
|
| Next Section: 1231.00 |