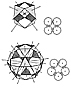
Fig. 465.00
 Rotation of Four Axes of Vector Equilibrium: Triangles,
Wheels, and
Cams
Rotation of Four Axes of Vector Equilibrium: Triangles,
Wheels, and
Cams
 Fig. 465.00 |
465.00  Rotation of Four Axes of Vector Equilibrium: Triangles,
Wheels, and
Cams
Rotation of Four Axes of Vector Equilibrium: Triangles,
Wheels, and
Cams
|
 Fig. 465.01 |
465.01
 We can have a vector equilibrium model made out of
a tubular steel frame
with each of the eight triangular faces connected by
four axes with a journal to slide on the
shafts and with each of the rods being perpendicular
to two of the eight triangular faces.
This is a four-dimensional, four-axis system. Just as
a regular tetrahedron has four unique
faces, so there are four unique perpendiculars to them,
making a four-dimensional system.
We can have a vector equilibrium model made out of
a tubular steel frame
with each of the eight triangular faces connected by
four axes with a journal to slide on the
shafts and with each of the rods being perpendicular
to two of the eight triangular faces.
This is a four-dimensional, four-axis system. Just as
a regular tetrahedron has four unique
faces, so there are four unique perpendiculars to them,
making a four-dimensional system.
|

|
465.02
 We can put a little rivet through the centers of area
of the eight triangles, and
we can let the brass rod run through the journals and
slide on a wire. We can tie the
corners of the triangles together with nylon threads.
If we spin the model rapidly on one of
the axes, all the triangles slide outwardly to form
the vector equilibrium. If next we touch
a finger or a pencil to any midface of one triangle
in the spinning system, the whole system
will contract symmelrically until it becomes an octahedron.
But when we take the finger or
pencil off again, centrifugal force will automatically
open up the system to the vector-
equilibrium condition again. The oscillating motion
makes this an expanding and
contracting system.
We can put a little rivet through the centers of area
of the eight triangles, and
we can let the brass rod run through the journals and
slide on a wire. We can tie the
corners of the triangles together with nylon threads.
If we spin the model rapidly on one of
the axes, all the triangles slide outwardly to form
the vector equilibrium. If next we touch
a finger or a pencil to any midface of one triangle
in the spinning system, the whole system
will contract symmelrically until it becomes an octahedron.
But when we take the finger or
pencil off again, centrifugal force will automatically
open up the system to the vector-
equilibrium condition again. The oscillating motion
makes this an expanding and
contracting system.
|
 Fig. 465.03 |
465.03
 We see that every one of the triangles in the vector
equilibrium can shuttle
back and forth, so that all the edges of the cube would
be arced outwardly with pairs of
arcing triangle corners shuttling in opposite directions
by each other. With a swiftly
oscillating system and a pulsating spherical expansion-contraction
going on everywhere
locally, the whole system becomes an optically pulsating
sphere. We find that each one of
the little triangles rotates as if it were swelling
locally. Each one of their vertexes brings
about a further spherical condition, so that in the
whole system, all the wires locally bend
outwardly temporarily to accommodate the whole motion.
We may now put together a
large omnidirectional complex of the sets of four-axis
and eight vertex-interconnected
transparent plastic triangles with alternate sets of
red transparent and uncolored
transparent plastic triangles. We can interconnect the
triangles from set to set. We then
find experimentally that if one force, such as a pencil,
is applied to one triangle of one
open vector equilibrium, that vector equilibrium closes
to become an octahedron, and vice
versa, throughout the whole system. Every vector equilibrium
will become an octahedron
and every octahedron will become a vector equilibrium.
(Which is to say that every space
becomes a sphere and every sphere becomes a space.)
We see that every one of the triangles in the vector
equilibrium can shuttle
back and forth, so that all the edges of the cube would
be arced outwardly with pairs of
arcing triangle corners shuttling in opposite directions
by each other. With a swiftly
oscillating system and a pulsating spherical expansion-contraction
going on everywhere
locally, the whole system becomes an optically pulsating
sphere. We find that each one of
the little triangles rotates as if it were swelling
locally. Each one of their vertexes brings
about a further spherical condition, so that in the
whole system, all the wires locally bend
outwardly temporarily to accommodate the whole motion.
We may now put together a
large omnidirectional complex of the sets of four-axis
and eight vertex-interconnected
transparent plastic triangles with alternate sets of
red transparent and uncolored
transparent plastic triangles. We can interconnect the
triangles from set to set. We then
find experimentally that if one force, such as a pencil,
is applied to one triangle of one
open vector equilibrium, that vector equilibrium closes
to become an octahedron, and vice
versa, throughout the whole system. Every vector equilibrium
will become an octahedron
and every octahedron will become a vector equilibrium.
(Which is to say that every space
becomes a sphere and every sphere becomes a space.)
|

|
465.04
 Since there is a force distribution lag in the system,
it is exactly like dropping
a stone into water and getting a planar pattern for
a wave, but in this one, we get an
omnidirectional wave. We can see the electromagnetic
wave pattern as clearly
demonstrated by one energy action in the system. This
may be the first time man has been
provided with omnidirectional conceptual comprehension
of the separate and combining
transformation events of local electromagnetic-wave-propagation
events.
Since there is a force distribution lag in the system,
it is exactly like dropping
a stone into water and getting a planar pattern for
a wave, but in this one, we get an
omnidirectional wave. We can see the electromagnetic
wave pattern as clearly
demonstrated by one energy action in the system. This
may be the first time man has been
provided with omnidirectional conceptual comprehension
of the separate and combining
transformation events of local electromagnetic-wave-propagation
events.
|

|
465.05
 We must remember that in the local water where we
drop the stone, the
molecules run inwardly and outwardly toward the center
of Earth gravitationally. The
water does not move; it accommodates a wave moving through
it. A wave inherently goes
outward in a pattern without any of the locally accommodating
molecules or atoms
migrating elsewhere. It is not simultaneous; we are
using our memory and afterimage. We
make a single energy action at one point and a complete
omnidirectional wave occurs.
This is similar to the steel-frame cube with all the
many triangles rotating in it.
(See Sec. 462 et seq.)
We must remember that in the local water where we
drop the stone, the
molecules run inwardly and outwardly toward the center
of Earth gravitationally. The
water does not move; it accommodates a wave moving through
it. A wave inherently goes
outward in a pattern without any of the locally accommodating
molecules or atoms
migrating elsewhere. It is not simultaneous; we are
using our memory and afterimage. We
make a single energy action at one point and a complete
omnidirectional wave occurs.
This is similar to the steel-frame cube with all the
many triangles rotating in it.
(See Sec. 462 et seq.)
|
 Fig. 465.10 |
465.10
 Wheels: Rubber Tires: If, instead of the eight triangular
faces of the vector
equilibrium, we substitute on the same shaft a little
automobile tire on a wheel, we can
bring tires in until each of the tires is frictionally
touching the other tires at three points. If
we have a train of gears, as one wheel goes one way,
the next wheel can go the other way
very comfortably. Around any hole there are four gears,
and since there are four__an even
number__we find that the trains reciprocate. There is
no blocking anywhere. When we
rotate one wheel in the light-wheel system, the other
wheels rotate responsively. They are
in friction with one another. Or we can hold on to the
bottom of one of the wheels and
turn the rest of the system around it. If we do so,
we find that the top wheel polarly
opposite the one we are holding also remains motionless
while all the other six rotate.
Wheels: Rubber Tires: If, instead of the eight triangular
faces of the vector
equilibrium, we substitute on the same shaft a little
automobile tire on a wheel, we can
bring tires in until each of the tires is frictionally
touching the other tires at three points. If
we have a train of gears, as one wheel goes one way,
the next wheel can go the other way
very comfortably. Around any hole there are four gears,
and since there are four__an even
number__we find that the trains reciprocate. There is
no blocking anywhere. When we
rotate one wheel in the light-wheel system, the other
wheels rotate responsively. They are
in friction with one another. Or we can hold on to the
bottom of one of the wheels and
turn the rest of the system around it. If we do so,
we find that the top wheel polarly
opposite the one we are holding also remains motionless
while all the other six rotate.
|

|
465.20
 Torus: If one of the mounted tires were just a rubber
doughnut, it could be
rotated inwardly like a torus; or it could be rotated
outwardly like a big atomic-bomb
mushroom cloud, opening in the center and coming in
at the bottom. This is what we call
an evoluting and involuting torus (see illustration
505.41, Pattern).
These rubber tires of
the eight-wheel assembly could not only rotate around
on each other, but it is quite
possible to make one wheel in such a way that it has
little roller bearings along its rim that
allow the rubber tires to rotate in the rim so that
the tire could be involuting and evoluting.
Therefore, if any one tire started to evolute, all the
other tires would reciprocate.
Torus: If one of the mounted tires were just a rubber
doughnut, it could be
rotated inwardly like a torus; or it could be rotated
outwardly like a big atomic-bomb
mushroom cloud, opening in the center and coming in
at the bottom. This is what we call
an evoluting and involuting torus (see illustration
505.41, Pattern).
These rubber tires of
the eight-wheel assembly could not only rotate around
on each other, but it is quite
possible to make one wheel in such a way that it has
little roller bearings along its rim that
allow the rubber tires to rotate in the rim so that
the tire could be involuting and evoluting.
Therefore, if any one tire started to evolute, all the
other tires would reciprocate.
|

|
465.21
 If we hold only an axis in our hand, we can rotate
the system around it. But
as we rotate it around, all the wheels are rolling.
As we saw in the pumping vector
equilibrium, the opposite triangles never torque in
relation to each other. The opposite
wheel of the one we are holding does the same. With
the bottom wheel stationary on the
ground and another wheel immobilized by one holding
it, we can rotate the system so that
one wheel rolls around the other. But we find that no
matter how much we move it
equatorially, if we immobilize one wheel in our fingers,
the one opposite it becomes
immobilized, too. If we not only hold a wheel immobilized
while another is turning, but
also squeeze and evolute it, all of the wheels will
also involute and evolute.
If we hold only an axis in our hand, we can rotate
the system around it. But
as we rotate it around, all the wheels are rolling.
As we saw in the pumping vector
equilibrium, the opposite triangles never torque in
relation to each other. The opposite
wheel of the one we are holding does the same. With
the bottom wheel stationary on the
ground and another wheel immobilized by one holding
it, we can rotate the system so that
one wheel rolls around the other. But we find that no
matter how much we move it
equatorially, if we immobilize one wheel in our fingers,
the one opposite it becomes
immobilized, too. If we not only hold a wheel immobilized
while another is turning, but
also squeeze and evolute it, all of the wheels will
also involute and evolute.
|

|
465.22
 It is quite possible to make an automobile tire and
mount it in such a way
that it looks triangular; that is, it will have a very
small radius in its corners. I can take the
same rubber and stretch it onto a triangular frame and
also have the same little roller
bearings so that it can involute and evolute. We will
have a set of triangular tires that will
pump from being the vector equilibrium into being the
octahedron and back again. If we
were then to immobilize one part of it, i.e., not let
it involute and evolute, the rest of the
system, due to rotation, would contract to become an
octahedron so that it makes all the
others reciprocate involuting and evoluting. We are
able then to immobilize one axis, and
the rest of the system except our opposite pole will
both rotate and involute-evolute
pulsatively.
It is quite possible to make an automobile tire and
mount it in such a way
that it looks triangular; that is, it will have a very
small radius in its corners. I can take the
same rubber and stretch it onto a triangular frame and
also have the same little roller
bearings so that it can involute and evolute. We will
have a set of triangular tires that will
pump from being the vector equilibrium into being the
octahedron and back again. If we
were then to immobilize one part of it, i.e., not let
it involute and evolute, the rest of the
system, due to rotation, would contract to become an
octahedron so that it makes all the
others reciprocate involuting and evoluting. We are
able then to immobilize one axis, and
the rest of the system except our opposite pole will
both rotate and involute-evolute
pulsatively.
|

|
465.30
 Four-Dimensional Mobility: We are now discovering
that in omnimotional
Universe, it is possible to make two moving systems
that move four-dimensionally,
comfortably, the way we see four sets of wheels (eight
wheels altogether) moving quite
comfortably. But if we fasten one vector equilibrium
to another by a pair of wheels__
immobilizing one of them and having an axis immobilized__the
rest of the system can keep
right on rolling around it. By fastening together two
parts of the Universe, we do not stop
the rest of the four-dimensional motion of Universe.
In all other non-four-dimensional
mechanical systems we run into a "three-dimensional"
blockage: if anything is blocked,
then everything is blocked. But in a four-dimensional
system, this is not at all the case. We
can have two atoms join one another perfectly well and
the rest of Universe can go right
on in its motion. Nothing is frustrated, although the
atoms themselves may do certain
polarized things in relation to one another, which begins
to explain a lot of the basic
experiences.
Four-Dimensional Mobility: We are now discovering
that in omnimotional
Universe, it is possible to make two moving systems
that move four-dimensionally,
comfortably, the way we see four sets of wheels (eight
wheels altogether) moving quite
comfortably. But if we fasten one vector equilibrium
to another by a pair of wheels__
immobilizing one of them and having an axis immobilized__the
rest of the system can keep
right on rolling around it. By fastening together two
parts of the Universe, we do not stop
the rest of the four-dimensional motion of Universe.
In all other non-four-dimensional
mechanical systems we run into a "three-dimensional"
blockage: if anything is blocked,
then everything is blocked. But in a four-dimensional
system, this is not at all the case. We
can have two atoms join one another perfectly well and
the rest of Universe can go right
on in its motion. Nothing is frustrated, although the
atoms themselves may do certain
polarized things in relation to one another, which begins
to explain a lot of the basic
experiences.
|

|
465.40
 Triangular-cammed, In-out-and-around Jitterbug Model
(Short Title)
Triangular-cammed, In-out-and-around Jitterbug Model
(Short Title)
|

|
465.41
 The four axes of the vector equilibrium provide the
four-dimensionally
articulatable model of motion freedoms unimpeded by
other motions of either contiguous
or remote systems of Universe while copermitting the
concurrently articulating both
omnidirectional wave propagation and gravitationally
convergent embracement. We can
also call it by the short title: triangular-cammed,
in-out-and-around jitterbug model. (See
Fig. 465.01.)
The four axes of the vector equilibrium provide the
four-dimensionally
articulatable model of motion freedoms unimpeded by
other motions of either contiguous
or remote systems of Universe while copermitting the
concurrently articulating both
omnidirectional wave propagation and gravitationally
convergent embracement. We can
also call it by the short title: triangular-cammed,
in-out-and-around jitterbug model. (See
Fig. 465.01.)
|

|
465.42
 The "opposite" of the engineers' equal-and-opposite
action and reaction is a
strictly 180-degree linear conceptioning, conceived
on a planar drawing. Macro is not
opposite to micro: these are opposed, inward-andoutward,
explosive-contractive,
intertransformative accommodations such as those displayed
by the eight-triangular-
cammed, perimeter-tangent, contactdriven, involuting-evoluting,
rubber doughnut
jitterbug. In such a model macro and micro are not planarly
opposed: they are the poles of
inwardoutward, omnidirectional, locally vertexing considerations
of experience. (See Fig.
465.10.)
The "opposite" of the engineers' equal-and-opposite
action and reaction is a
strictly 180-degree linear conceptioning, conceived
on a planar drawing. Macro is not
opposite to micro: these are opposed, inward-andoutward,
explosive-contractive,
intertransformative accommodations such as those displayed
by the eight-triangular-
cammed, perimeter-tangent, contactdriven, involuting-evoluting,
rubber doughnut
jitterbug. In such a model macro and micro are not planarly
opposed: they are the poles of
inwardoutward, omnidirectional, locally vertexing considerations
of experience. (See Fig.
465.10.)
|
| Next Section: 466.00 |